- Nullkurve
Nullkurve, Begriff der Lehre von den gesättigten Dämpfen in der Wärmetheorie.
Unter den gewöhnlichen Voraussetzungen der letzteren hat man bei beliebigen Zustandsänderungen von Dampf- und Flüssigkeitsgemischen für die pro Kilogramm zuzuführende Wärmemenge (Abfuhr = negative Zufuhr) nach Bd. 2, S. 542, mit den dortigen Bezeichnungen:
d Q = (1 – x) c d t + h x d t + r d x.
1.
c, die spezifische Wärme der Flüssigkeit, ist positiv (s. Flüssigkeitswärme, Spezifische Wärme), die Clausiussche Temperaturfunktion h (s.d.) innerhalb gewisser Grenzen negativ. Demnach wird es ein Mischungsverhältnis geben, bei welchem die für die (1 – x) kg Flüssigkeit zu- oder abzuführende Wärmemenge die für die x kg Dampf ab- oder zuzuführende Menge gerade deckt und d Q nur zur Verdampfung von dx dient:
d Q = r d x, c0 = dQ/dt = r dx/dt.
2.
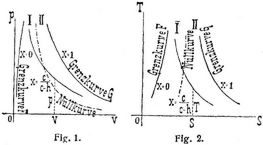
In den graphischen Darstellungen der Zustandsänderungen in der Wärmetheorie (Abszisse = Volumen v, Ordinate = Druck p, s. Aeußere Arbeit und Fig. 1; oder Abszisse = Entropie S, Ordinate = Temperatur T, s. Wärmetheorie und Fig. 2) heißt die Linie, auf welcher jenes Verhältnis dauernd eingehalten wird, die Nullkurve [1]. Man hat für sie neben 2.:
x = c/(c – h), v = x u + σ = cu/(c – h) + σ.
3.
Die Nullkurve teilt das ganze Gebiet des gesättigten Dampfes in zwei Teile I und II, c c für welche die spezifische Dampfmenge x < c/(c – h) bezw. x > c/(c – h) ist. Bei adiabatischer Expansion findet im Raum I Verdampfung, im Raum II Kondensation statt, bei adiabatischer Kompression gilt das Gegenteil, beim Durchschreiten der Nullkurve ist in beiden Fällen d x = 0. Bei Expansion mit konstanter spezifischer Dampfmenge x ist im Räume I Wärme zu entziehen, im Räume II Wärme zuzuführen, für Kompression bei konstantem x gilt das Gegenteil, beim Durchschreiten der Nullkurve ist in beiden Fällen d Q = 0. – Für Wasserdampf kann man innerhalb des Gebiets der Regnaultschen Versuche (s. Dampf, gesättigter) anstatt 3. setzen x = 0,338 + 0,00134 t, womit pro 1 kg v = (0,338 + 0,00134 t) u + 0,001, ferner d x : d t = 0,00134 konstant und die spezifische Wärme c0 = 0,00134 r proportional der Verdampfungswärme [1], [6]. Betreffs verschiedener Dämpfe s. [3].
Literatur: [1] Weyrauch, Zur Theorie der Dämpfe, Zeitschr. d. Ver. deutsch. Ing. 1876, S. 193. – [2] Fliegener, Vierteljahrschr. d. Naturforsch. Gesellsch. zu Zürich 1884, S. 226. – [3] Mollier, Das Wärmediagramm, Verhandl. d. Ver. s.d. Beförd. d. Gewerbefleißes 1893, S. 160. – [4] Ancona, Das Wärmediagramm der gesättigten Dämpfe, Zeitschr. d. Ver. deutsch. Ing. 1897, S. 447. – [5] Zeuner, Techn. Thermodynamik, II, Leipzig 1901, S. 96. – [6] Weyrauch, Grundriß der Wärmetheorie, II, Stuttgart 1907, S. 36, 41, 42.
Weyrauch.
http://www.zeno.org/Lueger-1904.