Bergzeichnung

Bergzeichnung, die Methode der Darstellung der Geländeformen durch Auszeichnung dicht nebeneinander liegender Fallinien in einer solchen Anordnung und Stärke, daß dadurch für jedes Teilchen einer topographischen Fläche Größe und Richtung der Böschung zum Ausdruck kommt.

Die Methode ist von dem sächsischen Major Lehmann 1794 [1] entwickelt worden und von da an allgemein an Stelle früher üblicher Darstellungsverfahren (der Hügelmanier und der älteren Schraffenmanieren, wie z.B. der v. Müllerschen ∫-Strich- und der sächsischen Kreuzstrichmanier) getreten. Das Prinzip ist das folgende: Durch Auszeichnen von Fallinien wird die Richtung des Gefälles für alle Punkte der Fläche angegeben und dieselbe gleichzeitig in Flächenelemente zerlegt (s. Fig. 1). Diese Auszeichnung der Fallinien geschieht entweder direkt im Gelände durch Schätzung (Kroki) oder Messung der Fallrichtung oder auf Grund einer besonderen Aufnahme und Horizontalkurvenkonstruktion (s. Nivellieren, Tachymetrie, Topographie). Um den Grad der Neigung dieser Flächenteile zum Ausdruck zu bringen, wird die Stärke der Beleuchtung, die Flächen beliebiger Neigung durch lotrecht einfallendes Licht erhalten, durch passende Anordnung der Stärke der Fallstricke (die man dann Bergstriche nennt) derart dargestellt, daß die Geländeformen je nach dem Grade ihrer Neigung schattiert (beleuchtet) erscheinen. Unter der Annahme vertikal einfallenden Lichtes würde ein horizontaler Flächenteil die volle Lichtmenge = 1 erhalten, eine vertikale Wand (Neigung α = 90º) gar kein Licht, also 0, dazwischen die Lichtmenge aber proportional dem Kosinus des Böschungswinkels α sein; da nun die Bergzeichnung für die Zwecke der Militärtopographie hauptsächlich dazu dienen soll, die Ersteigbarkeit des Geländes zum Ausdruck zu bringen, und starke Neigungen militärisch unzulänglich sind, hat Lehmann die Lichtmenge zwischen 0° und 45° Neigung so verteilt, daß horizontale Flächenteilchen weiß bleiben, unter 45° und steiler geböschte dagegen schwarz werden, und dazwischen schwarz S und weiß W nach der Gleichung:

S : W = α : (45° – α),

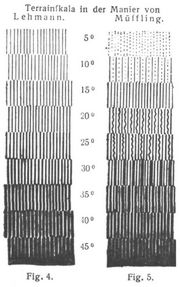
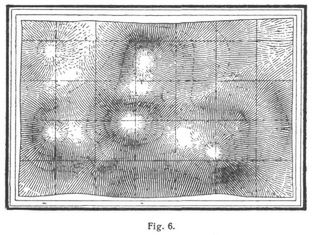
wie in Fig. 2 ausgedrückt ist, verteilt wird. Damit erhält man für die Neigungen von 5° zu 5° die Beziehungen S: W, die in Fig. 3 neben der Tonskala (Schraffierungsverhältnisse) angegeben sind. Nach diesen Grundsätzen hat Lehmann seine in Fig. 4 dargestellte Terrainskala entworfen. Der Abstand der Striche (Breite der Flächenelemente) richtet sich nach dem Maßstab[702] der Karte; so nimmt die preußische Landesaufnahme z.B. auf 1 cm beim Maßstab 1 : 25000 20–25 Striche, bei 1 : 100000 34–42 Striche. – Um die bei der Lehmannschen Skala schwierige Unterscheidung der Gradationen zu erleichtern, führte Müffling (1821) für einige derselben geschlängelte Striche ein und entwarf die Müfflingsche Terrainskala (Fig. 5). Nach diesen Grundsätzen wurden verschiedene Schraffenmethoden und Terrainskalen entworfen, so z.B. kombinierte die preußische Landesaufnahme die Lehmannsche und Müfflingsche zur sogenannten Generalstabsmanier [2], im Topographischen Atlas von Bayern wurde die Skala nach der Beziehung S : W = α : (60º – α), im österreichischen Militärgeographischen Institut S : W = α : (50º – α) eingeführt. Fig. 6 gibt ein Beispiel zur Anwendung der Bergzeichnung.

Literatur: [1] Lehmann, Darstellung einer neuen Theorie der Bezeichnung der schiefen Flächen im Grundriß oder der Situationszeichnung der Berge, Leipzig 1799. – [2] Instruktion für die Topographen der topographischen Abteilung der Königl. preußischen Landesaufnahme, Berlin 1876, Heft 1, § 126; Musterblätter für die topographischen Arbeiten der Königl. preußischen Landesaufnahme, 3. Aufl., Berlin 1885; Lehmann, Die Lehre der Situationszeichnung, herausgegeben von Becker und Fischer, 5. Aufl., Dresden und Leipzig 1843. Von den zahlreichen Anleitungen verschiedener Art seien nur noch genannt: Neutze, Theoretisch-praktische Schule des Situationszeichnens mit besonderer Berücksichtigung der Terraindarstellungen nach Modellen, Kassel 1859; Reitzner, Schule der Terraindarstellung, Wien 1881; Streffleur, Allgemeine Terrainlehre mit Beispielen zu deren praktischer Verwertung, Wien 1876.

Reinhertz.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4., Fig. 5.

Fig. 6.