Fresnels Spiegelversuch

Fresnels Spiegelversuch, der geschichtlich denkwürdige Versuch, durch den der französische Physiker Jean Augustin Fresnel 1816 [1] den schlagendsten experimentellen Beweis für die Richtigkeit der Wellentheorie des Lichtes lieferte, wodurch die von Newtons Schule vertretene Emanationstheorie dauernd zu Fall kam. Wenn das Licht kein Stoff, sondern eine Bewegung ist, die von den leuchtenden Körpern aus sich fortpflanzt, so muß es möglich sein, zweierlei Lichtschwingungen so zusammentreffen zu lassen, daß sie sich gegenseitig aufheben.

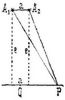
Thomas Young hatte schon die Beugungserscheinungen und die Farben dünner Blättchen in diesem Sinne als Erscheinungen der »Interferenz« von Wellen erklärt, diese Erscheinungen waren aber auch von der Emanationstheorie, wenn auch weniger überzeugend, zu erklären versucht worden. – Fresnel verschafft sich zwei Lichtquellen derart, daß beide genau übereinstimmend und gleichzeitig Lichtwellen gleicher Art aussenden. Er erreicht das in einfacher Weise dadurch, daß er das durch eine seine Spalte gehende, Licht einer am besten einfarbigen Lichtquelle von zwei Spiegeln reflektiert werden läßt. Die beiden Spiegelbilder der leuchtenden Spalte sind die zwei genau in der Phase der ausgesandten Wellen übereinstimmenden Lichtquellen. Indem man die Schnittlinie beider Spiegelebenen der Lichtlinie parallel Hellt und den Winkel der Ebenen nahe gleich 180° macht, erhält man die beiden Spiegelbilder parallel gerichtet und sehr nahe beisammen liegend. Es seien (s. die Figur) A₁ und A₂ die beiden Spaltenbilder im Abstande a von einander und es sei O P ein der Ebene beider Bilder paralleler Schirm in der Entfernung e von diesen Bildern; dann werden in der Linie O des Schirms, welche von A₁ und A₂ gleichen Abstand hat, die von A₁ und A₂ ausgehenden Wellen mit gleicher Phase, d.h. Wellenberge mit Bergen, Täler mit Tälern, zusammentreffen und in O eine helle Linie erzeugen. Eine Linie P aber rechts oder links von O wird entweder hell oder dunkel erscheinen, je nachdem die beiderlei Wellen sich daselbst mit gleicher oder mit entgegengesetzter Phase begegnen, d.h. je nachdem die Weglängen A₁ P – A₂ P sich um eine ganze Anzahl von Lichtwellenlängen unterscheiden oder um eine ganze Zahl plus einer halben Wellenlänge. Ist OP = d, so erkennt man leicht, daß

oder daß A₁ P – A₂ P = 2 a d/(A₁ P + A₂ P). Da bei dem Versuche nun a im Vergleich mit d klein und im Vergleich mit e sehr klein gemacht wird, so ist, falls man A₁ P – A₂ P = n λ setzt, sehr annähernd n λ = a d : e. Auch für eine kleine Anzahl n von Lichtwellenlängen λ erhält d noch einen meßbaren Betrag, wenn e im Vergleich mit a sehr groß genommen wird. Zählt man die Anzahl heller und dunkler Streifen, Interferenzfransen, zwischen O und P oder zwischen irgend zwei Streifen P, deren Abstand gleich d ist, so kann man aus den Werten von a, e, d und n den Wert λ bestimmen. – Der Fresnelsche Spiegelversuch gestattet, die Lichtwellenlänge zu messen. Statt der Spiegel kann man zur Erzeugung der zwei Lichtquellen auch das Fresnelsche Interferenzprisma anwenden oder nach Fizeau zwei geneigte Glasplatten, welche Parallelverschiebung des Bildes bewirken, oder nach Billet zwei Halblinsen. Vgl. darüber [2].

Literatur: [1] Oeuvres complètes d'Augustin Fresnel, I, S. 150, Paris 1866–70. – [2] Müller, Joh., Lehrbuch der Physik und Meteorologie, 8. Aufl., Bd. 2, S. 413, Braunschweig 1879.

Aug. Schmidt.