Hauptspannungen

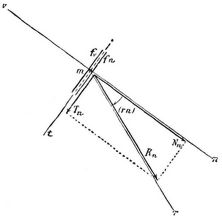
Hauptspannungen. In jedem Schnitte durch einen Körper kann man sich zwei Flächen zusammenhängend denken, auf welche im allgemeinen Kräfte gleicher Größe aber entgegengesetzter Richtung wirken (vgl. Bd. 3, S. 111, 389). Jede dieser Kräfte läßt sich in Komponenten normal und tangential den ergriffenen Flächenelementen zerlegen, deren Werte für die Flächeneinheit Normalspannungen und Tangentialspannungen oder auch im ersten Falle Zug- und Druckspannungen, im zweiten Schubspannungen heißen (Bd. 3, S. 111). Diese Spannungen erweisen sich, abgesehen von gewissen Unstetigkeitsschnitten (Risse, Gelenke, Gleitflächen u.s.w.), als stetige Funktionen des augenblicklichen oder auch des anfänglichen Orts der zugehörigen Flächenelemente (Bd. 3, S. 391; [9], II. und IV. Abschnitt); für alle einem Punkte m unendlich nahe liegenden Flächenelemente f_n ändern sie sich nur mit der Richtung n ihrer von m ausgehenden Normalen (s. die Figur). Werden die Spannungen so bezeichet, daß die Hauptbezeichnung ihrer Richtung, der Index der Normalenrichtung des ergriffenen Flächenelements entspricht (Bd. 3, S. 389), so bedeutet N_n die Normalspannung auf das Flächenelement der Normalenrichtung n. Die Maxima und Minima dieser Normalspannungen für die einem Punkte m anliegenden Flächenelemente werden Hauptspannungen daselbst genannt. Es bestehen im allgemeinen drei verschieden e Hauptspannungen A, B, C, die nach Absolutwert und Richtung den Halbachsen eines Ellipsoids um m entsprechen (s. Spannungsellipsoid). Die Flächenelemente, welche durch Hauptspannungen beansprucht werden, besitzen keine Schubspannungen.

Es sei ein beliebiges rechtwinkliges Koordinatensystem gewählt; dann sind nach obiger Festsetzung

(ziehende Normalspannungen positiv). Sind diese Komponenten für Flächenelemente normal irgend drei zueinander senkrechten Richtungen x, y, z bekannt, so ergeben sich die Hauptspannungen als die drei Wurzeln h = A, h = B, h = C der Gleichung:

welche auch wie folgt geschrieben werden kann:

Die Winkel einer beliebigen Richtung n mit den positiven Richtungen x, y, z seien (n x), (n y), (n z). Substituiert man einen der Werte h = A, B, C in

so folgen aus

mit den beiden Vorzeichen von

die beiden einander entgegengesetzten Normalenrichtungen n (entsprechend n und υ in Figur) derjenigen Flächenelemente, welche durch diese Hauptspannung beansprucht werden. Für a le beliebigen zu einander senkrechten x, y, z sind von gleichen Werten:

Hiernach ist eine der Hauptspannungen A, B, C gleich Null, wenn für beliebige zueinander rechtwinklige Achsen:

es sind zwei Hauptspannungen gleich Null, wenn neben 9. gilt:

[792] und sind alle drei Hauptspannungen gleich Null, so hat man noch:

Verschwindet eine Hauptspannung, so folgt aus 2. mit 9. zur Berechnung der beiden übrigen:

verschwinden zwei Hauptspannungen, so liefert 12. mit 10. für die verbleibende:

und ist auch die dritte Hauptspannung gleich Null, so existieren bei dem betreffenden Punkte überhaupt keine Spannungen. In obigen Gleichungen ist den üblichen Voraussetzungen entsprechend gesetzt [9], S. 30, 125, 143:

was auch im folgenden geschehen wird.

In vielen Fällen ist von vornherein bekannt oder angenommen, daß alle einer bestimmten Ebene parallelen Flächenelemente nur von Normalspannungen oder gar nicht beansprucht werden (bei der Biegung gerader und einfach gekrümmter Stäbe die Flächenelemente parallel der Biegungsebene, bei Untersuchung des Erddrucks auf Stützmauern diejenigen parallel dem Mauerquerschnitt u.s.w.). Werden dann, wie üblich, die Achsen der x, y parallel jener Ebene, aber sonst beliebig gewählt, so sind in obigen Gleichungen X_z = Z_x = 0, Y_z = Z_y = 0, C bildet eine Hauptspannung, während sich die zwei übrigen aus

mit den beiden angedeuteten Vorzeichen ergeben. Setzt man in

für h den Wert einer der Hauptspannungen A, B, so folgen mit den beiden Vorzeichen die einander entgegengesetzten Normalenrichtungen derjenigen zwei Flächenelemente, welche durch diese Hauptspannung ergriffen sind. Bezeichnet α = (nx) + 90° den positiven, von 0 bis 360° variierenden Winkel der Spur eines Flächenelements senkrecht der xy-Ebene mit der positiven Richtung der x-Achse, so hat man auch:

Setzt man hierin h = A, so ergibt sich die Richtungslinie der durch A beanspruchten Flächenelemente und der Hauptspannungen B; setzt man h = B, so findet sich die Richtungslinie der von B ergriffenen Flächenelemente und der Hauptspannungen A. Unter den gewöhnlichen Voraussetzungen der Biegungstheorie gerader und einfach gekrümmter Stäbe (s. Biegung) hat man, wenn die x-Achse bei Anwendung obiger Beziehungen parallel der Stabachse gelegt wird, mit X_x = σ, X_y = τ, Y_y = 0:

Die drei Hauptspannungen sind in diesem Falle:

Ueber σ, τ s. Bd. 1, S. 792, 798. Vgl. Spannungstrajektorien. Ueber reduzierte Hauptspannungen s. Festigkeitsbedingung, Bd. 3, S. 716.

Ableitung vorstehender Gleichungen [9], §§ 14, 18, weitere Beziehungen für Hauptspannungen und Anwendungen [9], §§ 14–18, [10], A. 15–21. Für vollkommene Flüssigkeiten sind die Spannungen auf alle beliebig gerichteten Flächenelemente bei einem Punkte m gleich große Normalspannungen und also auch A = B = C = – p, [9], §§ 45, 63. Ausdrücke der Spannungen durch die Verschiebungen für andre isotrope Körper s. Bd. 3, S. 391.

Literatur: [1] Lame, Leçons sur la theorie mathematique de l'élasticité des corps solides, Paris 1852, S. 56 (auch 1866, S. 56). – [2] Clebsch, Theorie der Elastizität fester Körper, Leipzig 1862, S. 16. – [3] Navier, De la résistance des corps solides, avec des notes et des appendices de Saint-Venant, Paris 1864, S. 774. – [4] Winkler, Die Lehre von der Elastizität und Festigkeit, Prag 1867, S.S. – [5] Kirchhoff, Vorlesungen über mathematische Physik, Mechanik, Leipzig 1877, S. 115. – [6] Klein, Theorie der Elastizität, Akustik und Optik, Leipzig 1877, S. 16. – [7] Grashof, Theorie der Elastizität und Festigkeit, Berlin 1878, S. 10. – [8] Mohr, Ueber die Darstellung des Spannungszustandes und des Deformationszustandes eines Körperelements, Civilingenieur 1882, S. 113. – [9] Weyrauch, Theorie elastischer Körper, Leipzig 1884, S. 14, 45. – [10] Ders., Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 29 u.s.w. – [11] Neumann, Vorlesungen über die Theorie der Elastizität der festen Körper und des Lichtäthers, Leipzig 1885, S. 26. – [12] Brauer, Festigkeitslehre, Leipzig 1905, S. 13, 19, 27. – Weitere Literatur s. Elastizitätslehre, allgemeine.

Weyrauch.