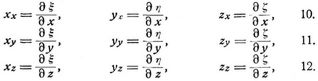Hauptverschiebungen

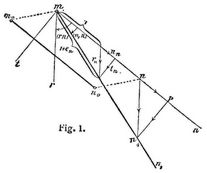
Hauptverschiebungen. Wenn ein Punkt n sich bezüglich eines Punktes m bewegt, so heißen die relativen Wege von n gegen m für die Einheit der anfänglichen Entfernung mn Verschiebungen von n gegen m (Bd. 3, S. 390). Sind die Punkte m, n aus den anfänglichen Lagen m₀, n₀ nach m, n gelangt und denkt man sich von m aus in der ursprünglichen Richtung n des Punktes n (Fig. 1) die Entfernung m₀, n₀ = mn angetragen, so ist nn₁ der Weg, welchen n hinsichtlich m zurückgelegt hat. In Fig. 1 ist die Darstellung dieser Verhältnisse der Klarheit halber auf die Ebene beschränkt. Verlängert man die Gerade mn bis zum Punkte p, aufweichen das Perpendikel aus n₁ trifft, so sind np und pn₁ die relativen Wege des Punktes n in der ursprünglichen Richtung von m aus und senkrecht zur selben, während

die Normalverschiebung, Transversalverschiebung und Totalverschiebung ausdrücken. Dabei kann n_n positiv oder negativ sein (je nachdem mp größer oder kleiner als mn ist). Da man die Richtung des Punktes n von m aus auf ein Koordinatensystem beziehen muß, so werden n_n, t_n, r_n von der Bewegung der Punkte m, n in Hinsicht desselben abhängig (im Gegensatze zu den Dehnungen, s.d., Bd. 2, S. 692). In einem Körper können bezüglich eines Körperpunktes m alle andern Körperpunkte n Verschiebungen erleiden. Dieselben lassen sich erfahrungsgemäß innerhalb gewisser Grenzen als stetige Funktionen des anfänglichen Orts der Punkte m, n ansehen, abgesehen von möglichen Unstetigkeitsschnitten (Risse, Gelenke, Gleitflächen u.s.w.), derart, daß sie für alle m unendlich benachbarten Punkte n nur von deren anfänglichen Richtungen von m aus abhängen (Bd. 3, S. 390). Die Maxima und Minima der Normalverschiebungen n_n bei einem Punkte m heißen Hauptverschiebungen daselbst. Es existieren im allgemeinen drei verschiedene Hauptverschiebungen a, b, c, welche Punkten auf drei anfänglich zueinander senkrechten Richtungslinien (oder sechs zueinander senkrechten Richtungen) entsprechen.

Werden die Verschiebungen so bezeichnet (Fig. 1), daß die Hauptbezeichnung deren Richtung, der Index der anfänglichen Richtung des verschobenen Punktes vom Bezugspunkte m aus entspricht, so hat man

Sind diese Komponenten für drei beliebige zueinander senkrechte Richtungen x, y, z bekannt, so ergeben sich mit den Bezeichnungen:

[794] die Hauptverschiebungen als die drei Wurzeln h = a, h = b, h = c der Gleichung:

welche auch geschrieben werden kann:

Die Winkel einer beliebigen Richtung n mit den (positiven) Richtungen x, y, z seien (nx), (ny), (nz). Substituiert man einen der Werte h = a, b, c in

so folgen aus

mit den beiden Vorzeichen von

die beiden einander entgegengesetzten Richtungen n, für welche diese Hauptverschiebung eintritt. Für alle beliebigen zueinander senkrechten Richtungen x, y, z sind von gleichen Werten:

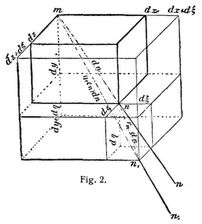
wonach sich, wie bei den Hauptspannungen (s.d.), diejenigen Beziehungen und Vereinfachungen ergeben, welche eintreten, wenn eine, zwei oder drei Hauptverschiebungen gleich Null sind. Bezeichnen ξ, η, ζ die Wege eines Körperpunktes m bei x, y, z in den Richtungen x, y, z, so sind in obigen Gleichungen (Bd. 3, S. 390, Fig. 2):

Ableitung obiger Gleichungen [3], §§ 21, 23, weitere Beziehungen betreffend die Hauptverschiebungen [3], §§ 23, 30–32, 48, 49, 57, und [4], A. 25, 27, 31, 33. Die Hauptverschiebungen gewinnen in der allgemeinen wie technischen Elastizitätslehre dadurch an Bedeutung, daß nur solche Bewegungen innerhalb der betrachteten Körper untersucht zu werden pflegen, für welche die Dehnungen e_n (Fig. 1, 2) gleich den Normalverschiebungen n_n gesetzt werden, womit auch die Hauptverschiebungen anstelle der Hauptdehnungen treten. Vgl. a. Dehnung, Bd. 2, S. 692, Festigkeitsbedingung, Bd. 3, S. 716, und [3], §§ 30, 32. Bezüglich der Bedeutung der Summe 7. s. Dilatation. Ausdrücke der Verschiebungen durch die Spannungen für isotrope Körper Bd. 3, S. 391.

Literatur: [1] Navier, De la resistance des corps solides, avec des notes et des appendices de Saint-Venant, Paris 1864, S. 549, 779. – [2] Kirchhoff, Vorlesungen über mathematische Physik, Mechanik, Leipzig 1877, S. 96. – [3] Weyrauch, Theorie elastischer Körper, Leipzig 1884, S. 60, 83 u.s.w. – [4] Ders., Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 55, 58 u.s.w. – [5] Neumann, Vorlesungen über die Theorie der Elastizität der festen Körper und des Lichtäthers, Leipzig 1885, S. 37. – [6] Mathieu, Theorie de l'élasticité des corps solides, Paris 1890, S. 22. – [7] Poincaré, Leçons sur la theorie de l'élasticité, Paris 1892, S. 10. – [8] Voigt, Kompendium der theoretischen Physik, I, Leipzig 1895, S. 211. – Weitere Literatur s. unter Elastizitätslehre, allgemeine.

Weyrauch.

Fig. 1.

Fig. 2.