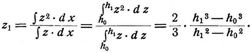Hydrostatik

Hydrostatik, die Lehre vom Gleichgewicht der Flüssigkeiten; sie bildet einen Spezialfall der Hydrodynamik, wenn angenommen wird, daß sich eine Flüssigkeit in relativer Ruhe befinde.

Für diesen Fall werden in den S. 157 aufgestellten Fundamentalgleichungen 1 die Werte der Geschwindigkeiten u, v, w gleich Null und man hat:

wobei X, Y, Z die in Richtung der Achsen wirkenden auf die Masseneinheit bezogenen Komponenten der äußeren Kräfte, μ die Masse der Volumeneinheit (Dichte vgl. Bd. 2, S. 740), p die im Punkte x, y, z herrschende Pressung pro Flächeneinheit bedeuten. Multipliziert man die erste der Gleichungen 1. mit d x, die zweite mit d y, die dritte mit d z und addiert, so ergibt sich, weil

Die Integration dieser Gleichung liefert die Pressung als Funktion der Koordinaten x, y, z, wenn für einen bestimmten Zustand an einer bestimmten Stelle die Pressung bekannt ist, also die bei der Integration entstehende Konstante ermittelt werden kann. Für d p = 0, also p = c ergeben sich die sogenannten Niveauflächen, in welchen die Pressung überall einen konstanten[160] Wert annimmt (Flächen gleicher Pressung). Die zu 2. gehörigen Erörterungen allgemeiner Natur wollen in [1], S. 285 ff., nachgesehen werden.

Ohne Rücksicht auf Wärmebewegung und Molekularkräfte nimmt in einer relativ ruhenden Flüssigkeit nur die Schwerkraft (welche auf die Masseneinheit bezogen = g ist) Einfluß auf die Pressung; es wird dann X = 0, Y = 0, und, sofern man die Z-Achse positiv in Richtung der Schwere wählt, Z = g. Somit ergibt sich aus 2.

d p = μ g d z = γ d z.

3.

unter γ das Gewicht der Volumeneinheit der Flüssigkeit verstanden (vgl. Bd. 2, S. 740). Bei Annahme eines konstanten Wertes von γ (unzusammendrückbare Flüssigkeit und Vernachlässigung der Wärmewirkung) liefert die Integration mit den zusammengehörigen Anfangswerken p = p₀, z = h:

p – p₀ = γ (z – h).

4.

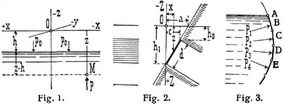
Aus dieser Gleichung ersieht man ohne weiteres, daß, weil anläßlich der Annahme für die Z-Achse die XY-Ebene horizontal sein muß, alle Niveauflächen horizontale Ebenen sind, mithin auch der Spiegel der Flüssigkeit. Ist der letztere (vgl. Fig. 1) dem atmosphärischen Drucke p₀ ausgesetzt, so nennt man in bezug auf den Punkt M, wenn p₀ = γ h, z = p : γ die Druckhöhe und z – h = (p – p₀) : γ die Ueberdruckhöhe (vgl. Bd. 3, S. 123).

Für die Technik von größter Bedeutung sind die Pressungen, welche das ruhende Wasser auf die Wände der einschließenden Gefäße ausübt. Ist in diesem Falle, wie gewöhnlich, die gedrückte Fläche beiderseits mit der atmosphärischen Pressung belastet, so kommt für die resultierende Pressung nur der Ueberdruck y (z – h) in Betracht. Verlegt man den Koordinatenanfang in den Spiegel der Flüssigkeit, versteht man also jetzt unter z die Tiefe des gedrückten Flächenelementes d F unter dem Spiegel, so ist die normal gegen dieses eben gedachte Element gerichtete, von der Ueberdruckhöhe z herrührende Wasserpressung d p:

d p = γ z d F.

5.

Wir werden nun im folgenden die wichtigsten, mit Hilfe dieser Formel lösbaren Probleme der Wasserpressung gegen Gefäßwände berechnen.

1. Wasserpressung gegen ebene oder zylindrische Wandflächen, die in Richtung der mit dem Spiegel des Wassers parallelen Erzeugenden eine konstante Breite b haben. – Das obere Ende einer ebenen Fläche liege in der Tiefe h₀, das untere in h₁ unter Spiegel (Fig. 2); die Länge der Fläche sei = d, ihre konstante Breite senkrecht zur XZ-Ebene = b. Entsprechend der Figur wird:

x = a (h₁ – z) : h₁; z = h₁ (a – x) : a; a d z = – h₁ · d x.

Das vom Wasser gedrückte Flächenelement in der Richtung der X-Achse ist = b d z; jenes in Richtung der Z-Achse = b d x. Man hat also für die Komponenten der Pressung P:

mithin:

Der Angriffspunkt der Resultanten ist bestimmt, wenn man die Ordinate z₁ desselben ermittelt. Letztere findet sich als Mittelpunkt der Parallelkräfte P_z aus der Gleichung

Nachdem F = b d die Größe der gedrückten Fläche, (h₁ + h₀) : 2 der vertikale Abstand ihres Schwerpunktes vom Spiegel ist, ergibt sich die Regel: Die Pressung auf eine ebene Fläche ist gleich dem Produkte aus dem Gewichte einer Wassersäule von der Basis F und einer Höhe gleich dem Vertikalabstande des Schwerpunktes von F unter Spiegel.

Ist die Fläche gekrümmt, so muß eine Gleichung der im Schnitte der XZ-Ebene entstandenen Leitlinie des Zylinders bestehen, welche für die ganze Fläche oder einen beliebigen Teil derselben die Komponenten P_x, P_z der Pressung und ihre Angriffspunkte x₁ und z₁:

P_x = γ b ∫ z d z, P_z = γ b ∫ z d x, x₁ = ∫ x z · dz : ∫ z d z, z₁ = ∫ z² d x : ∫ z d x

ermitteln läßt. Diesbezügliche Rechnungen sind zwar einfach, aber unbequem. Man ermittelt deshalb die Wasserpressungen auf gekrümmte Flächen in der Regel annähernd, und zwar dadurch, daß man die in der XZ-Ebene als Schnittlinie erscheinende Kurve A B C D E (Fig. 3) in ein Polygon mit den Ecken A B C D E umwandelt, die Pressungen gegen die so gedachten ebenen Flächen aus dem Angriffspunkte nach der vorhergehenden Methode feststellt und sodann die Zusammensetzung der verschiedenen P graphostatisch vornimmt. Die Methode ist übersichtlich und gewährt größere Sicherheit gegen Irrtümer als das rein analytische Verfahren.

2. Wasserpressungen gegen ebene Flächen, welche senkrecht zur XZ-Ebene nicht überall die gleiche Breite b haben. Legt man das Koordinatensystem so, daß der Ursprung in die Schnittlinie der ebenen Fläche mit dem Spiegel fällt und die XZ-Ebene senkrecht auf dieser die Y-Achse bildenden Schnittlinie steht, so ist nach dem vorhergehenden jedenfalls die Pressung P gegen die Fläche F : P = γ ∫ z · d F = γ F s, unters den Vertikalabstand des Schwerpunktes unter Spiegel verstanden. Ferner sind die Momente der Elementarpressungen in bezug[161] auf die Ebene der YZ : γ x z · d F, auf die Ebene der XZ : γ y z · d F, auf die Ebene der XY : γ z² d F. Hieraus ergeben sich die Koordinaten des Angriffspunktes der Gesamtpressung P:

x₁ = ∫ x z · d F : F s; y₁ = ∫ y z · d F : F s; z₁ = z² · d F : F s.

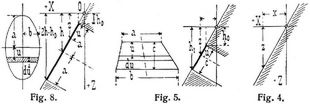
Außerdem besteht infolge der Wahl des Koordinatensystems (Fig. 4) die allgemeine Beziehung x = m z, also x₁ = m z₁.

Hat die Fläche F eine Symmetrielinie oder Mittellinie, in welche der Druckmittelpunkt notwendigerweise fallen muß, so genügt es, die Koordinate z₁ zu berechnen. Dies ist z.B. der Fall bei einem Trapez, dessen parallele Seiten a und b mit der Y-Achse parallel sind (Fig. 5). Für diese Figur ist u (h₁ – h₀) = c (z – h₀), also (h₁ – h₀) · d u = c · d z. Das Flächenelement wird: d F = (a + (b – a)/c)d u, und wenn man u und d u aus der vorhin gefundenen Beziehung ersetzt, so folgt: d F = [a h₁ – b h₀ + (b – a) z] · (c d z)/(h₁ – h₀)² womit:

gefunden wird. Die z-Koordinate des Angriffspunktes von P ermittelt sich zu:

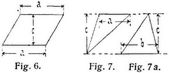
Wird a = b, d.h. ändert sich das Trapez in ein Parallelogramm von der Höhe c und der Grundlinie a (Fig. 6), so wird:

Wird b = 0, d.h. ändert sich das Trapez in ein auf der Spitze stehendes Dreieck (Fig. 7), so ist:

Mit a = 0 ergibt sich ein auf der Grundlinie stehendes Dreieck (Fig. 7a), wofür:

Weitere Vereinfachungen ergeben sich mit h₀ = 0, d.h. wenn die obere Seite des Trapezes mit der Y-Achse zusammenfällt, und c = h₁ – h₀, d.h. wenn die gedrückte Fläche des Trapezes vertikal steht; sie sind leicht zu finden.

Für eine elliptische Fläche, deren kleine Achse b mit der Y-Achse parallel geht und deren Mittelpunkt in der Tiefe h, deren Scheitel in h₀ unter der Abszissenachse (Fig. 8) liegen, bestehen die Beziehungen:

da die Ebene der X Z die große Achse der Fläche enthält. Aus der Figur ergibt sich ferner: u (h – h₀) = a (h – z). Es wird demgemäß:

und man erhält für z₁:

Selbstverständlich gelten diese Resultate auch für den Kreis von Radius R, wenn b = a = R gesetzt wird.

Es ist zu beachten, daß der Wasserdruck stets normal gegen die gedrückte Fläche gerichtet ist, also in vielen Fällen auch als Auftrieb (s.d.) wirkt. Wasserpressungen auf gekrümmte Flächen lind nicht parallel und lassen sich nicht immer auf eine Resultierende reduzieren. Der Angriffspunkt der resultierenden Wasserpressung und der Schwerpunkt der gedrückten Fläche fallen nur bei horizontaler Lage der letzteren zusammen; bei geneigten Flächen liegt der gedachte Angriffspunkt stets tiefer als der Schwerpunkt.

Literatur: [1] Grashof, F., Hydraulik, Leipzig 1875. – [2] Lueger, O., Wasserverforgung der Städte, Darmstadt 1895, woselbst reichliche, chronologisch geordnete Literaturangaben.

Lueger.

Fig. 1., Fig. 2., Fig. 3.

Fig. 6., Fig. 7., Fig. 7a.

Fig. 4., Fig. 5., Fig. 8.