- Kettenlinie
Kettenlinie ist die Gleichgewichtsfigur eines homogenen schweren Fadens (s. Fadenkurven).
Sie ist eine transzendente Kurve, deren Gleichung in rechtwinkligen Koordinaten
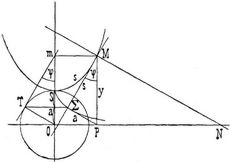
ist, worin die Konstante a der Parameter der Kurve heißt. Die Achse der y ist eine Symmetrielinie derselben, während sie selbst nur auf der einen Seite der x-Achse liegt. Die Symmetrielinie wird Achse, die x-Achse aber Leitgerade der Kettenlinie genannt. Die Ordinate y wächst für positive wie für negative x ins Unendliche und hat ein Minimum y = a für x = 0. Der Punkt des Minimums der Ordinate heißt der Scheitel S (s. die Figur).
Die Länge s des vom Scheitel an gerechneten Bogens ist:
Man erkennt leicht, daß y2 – s2 = a2 und s/a = d y/d x = cotg ψ ist, wenn ψ den Winkel bezeichnet, den die Tangente der Kurve mit der Richtung der Ordinaten bildet. Wickelt man daher den Bogen s mit der Tangente ab, so ist Σ M = s, und verbindet man Σ mit dem Fußpunkte P der Ordinate, so ist Δ M P Σ bei Σ rechtwinklig und P Σ = a. Beschreibt man daher um den Ursprung O mit α als Radius einen Kreis und projiziert den Punkt Σ parallel der x-Achse auf diesen, so ist die Tangente T m dieses Kreises in dem Projektionspunkte T parallel der Tangente der Kettenlinie in M. Der Krümmungshalbmesser ρ in M genügt der Gleichung ρ sin2 ψ = α. Daher ist derselbe gleich der Normalen M N vom Kurvenpunkte bis zur Leitgeraden. Der Punkt Σ beschreibt eine Evolvente der Kettenlinie, deren Tangente Σ P = a ist. Diese Evolvente ist daher eine Tractrixkurve mit O N als Leitgeraden, d.h. eine Kurve, für welche die Länge der Tangente, vom Berührpunkt bis zur Leitgeraden gerechnet, konstant ist.
[459] Kettenlinie gleicher Beanspruchung. Bei der gewöhnlichen Kettenlinie ist die Spannung im Scheitel am geringsten, und zwar gleich dem Gewicht eines Stücks der Kette von der Länge a. Im Punkte M ist die Spannung gleich dem Gewicht eines Stücks Kette von der Länge √(s2 + a2). Wird die Kette an den verschiedenen Stellen – der infolge ihres Gewichtes und Durchhanges dort herrschenden Spannung entsprechend – verschieden stark gemacht, so nimmt sie die Form einer Kettenlinie gleicher Beanspruchung an, deren Gleichung lautet: y = – b logn cos x/b, wo b die zulässige Reißlänge der Kette bedeutet.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.