- Kompressionskoeffizient
Kompressionskoeffizient. Wirkt auf die ganze Oberfläche eines Körpers lediglich ein gleichmäßig verteilter Normaldruck von p pro Flächeneinheit und[582] es findet bei konstanter Temperatur durch eine Aenderung ∂p von p eine Aenderung ∂v/v der Volumeneinheit statt, so heißt
der Kompressionskoeffizient des betreffenden Körpers [15], S. 71, wonach derselbe auch annähernd die Volumenabnahme pro Volumeneinheit, – Δv/v, durch die Druckzunahme Δp = 1 bei konstanter Temperatur bedeutet (gewöhnliche Definition). Häufig wird γ als Kompressibilität bezeichnet (der Ausdruck scheinbare Kompressibilität bezieht sich auf den aus Versuchen erhaltenen Wert von y, vor Berücksichtigung erkannter Fehlerquellen).
Wird anstatt des im allgemeinen veränderlichen Kompressionskoeffizienten γ ein mittlerer Kompressionskoeffizient γ' eingeführt, welcher von p1 bis p die gleiche Volumenänderung v – v1 wie der wirkliche bedingt, so hat man nach 1.:
und mit Rücksicht auf die Reihe für logn, wenn die Volumenänderungen so klein sind, daß das Quadrat und höhere Potenzen von v – v1/v1 gegen letzteren Wert vernachlässigt werden dürfen 1151, S. 72:
In 1.–3. können unter v, v1 die Volumen der Gewichtseinheit oder die ganzen Volumen des betrachteten Körpers verbanden werden. Beziehungen zwischen γ und andern Koeffizienten (Ausdehnungskoeffizient, Spannungskoeffizient) s. z.B. [1], S. 476, [15], S. 72.
Für Gase und Dämpfe werden die Volumenänderungen am einfachsten aus der Zustandsgleichung und verwandten Beziehungen berechnet. S. Boyle-Gay-Lussacsches Gesetz, Gase, gasförmige Körper, Dampf, gesättigter und überhitzter, oder [15], I und II.
Für Wasser hat man nach Grassi (Annales de chimie et de physique 1837, XXXI, S. 437) z.B.
wonach die Zusammendrückung von 1 cbm Wasser von 5,34 Atmosphären Druck und 18° Temperatur durch eine Druckerhöhung von 1 Atmosphäre (zu 1,0333 kg pro Quadratzentimeter) gleich 0,0000462 cbm und durch 50 kg pro Quadratzentimeter, wenn γ' = γ gesetzt wird, nach 3.:
(v1 – v)/v1 = 0,0000462 50/1,0333 = 0,00224 cbm = 2,24 l.
Violle gab auf Grund der Versuche von Grassi für gewöhnliche Drucke [10], S. 508:
γ = 0,0000503 + 0,0000013185 t – 0,00000003734 t2,
und Röntgen [3], S. 660, erhielt für 18° genau wie Grassi γ = 0,0000462. Bei höheren Drücken hat Amagat Versuche angestellt [11]. Er erhielt für 10000000 γ'
und insbesondere
Bei sehr hohen Drücken können bedeutend kleinere Kompressionskoeffizienten maßgebend sein, wie folgende von Amagat [8] erhaltenen Werte von 10000000 γ' bei 0° zeigen.
Zahlreiche Versuche sind über die Kompressibilität des Quecksilbers angestellt worden. Es erhielten bei wenig von 0° verschiedener Temperatur: Regnault 0,00000352, Grassi 0,00000295, Tait 0,0000036, Amagat 0,0000039, de Metz 0,00000374, wonach Quecksilber von allen Flüssigkeiten die kleinste bekannte Kompressibilität besitzt. De Metz [9] konnte für Quecksilber von 0 bis 19,4° ausdrücken:
γ = 0,00000374 + 0,0000000877 t.
[583] Näheres und weitere Kompressionskoeffizienten von Flüssigkeiten s.u.a. [7], S. 359, [10], S. 508, [12], S. 265, [13], S. 326, 330, 333.
Für elastische Volumenänderungen isotroper fester Körper liefert die Elastizitätslehre [2], S. 170, [7], S. 224, [13], S. 235, bei konstanten Werten des Elastizitätsmoduls E (s.d.) und des Elastizitätsquotienten ε (s.d.) mit μ = 1/ε:
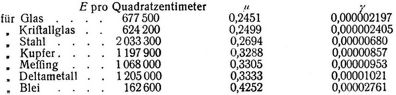
worin unter gewissen Voraussetzungen (s. hierüber und über Werte von ε, μ, unter Elastizitätsquotient) ε = 4, μ = 0,25 wäre. Amagat erhielt durch Versuche für p, E in Atmosphären, d.h. in Einheiten von 1,0333 kg pro Quadratzentimeter, auf Grund von 4. [6]:
und ohne Anwendung von Elastizitätsformeln [4]:
wonach die festen Körper im allgemeinen weit weniger kompressibel als die Flüssigkeiten sind und ihre Kompressibilität mit μ zu wachsen scheint. Werte von γ für andre feste Körper s.u.a. [12], S. 103.
Literatur: [1] Rühlmann, Handbuch der mechanischen Wärmetheorie, I, Braunschweig 1876, S. 466. – [2] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 170, 173. – [3] Röntgen und Schneider, Ueber die Kompressibilität des Wassers, Wiedemanns Annalen 1888, XXXIII, S. 644. – [4] Amagat, Compressibilité du mercure et du verre, Compt. rend. 1889, CVIII, S. 228. – [5] Ders., Determination directe de la compressibilité du verre, du cristal et des métaux, jusqu'à 2000 at, ebend. 1889, CVIII, S. 729. – [6] Ders., Recherches sur l'élasticité des solides, ebend. 1889, CVIII, S. 1199. – [7] Winkelmann, Handbuch der Physik, I. Allgemeine und spezielle Mechanik, Akustik, Breslau 1891, S. 220, 224, 355. – [8] Amagat, Sur les lois de compressibilité des liquides, Compt. rend. 1892, CXV, S. 638,919. – [9] De Metz, Ueber die absolute Kompressibilität des Quecksilbers, Wiedemanns Annalen 1892, XLVII, S. 706. – [10] Violle, Lehrbuch der Physik, I, Mechanik, Berlin 1893, S. 497. – [11] Amagat, Dilatation et compressibilité de l'eau, Compt. rend. 1893, CXVI, S. 41. – [12] Landolt und Börnstein, Physikalischchemische Tabellen, Berlin 1894, S. 265. – [13] Wüllner, Lehrbuch der Experimentalphysik, I, Allgemeine Physik und Akustik, Leipzig 1895, S. 235, 317. – [14] Chwolson, Lehrbuch der Physik, I, Braunschweig 1902, S. 547, 719. – [15] Weyrauch, Grundriß der Wärmetheorie, I, Stuttgart 1905, S. 71; II, Stuttgart 1907, S. 380.
Weyrauch.
http://www.zeno.org/Lueger-1904.