Boyle-Gay-Lussacsches Gesetz

Boyle-Gay-Lussacsches Gesetz oder Mariotte-Gay-Lussacsches Gesetz. Dasselbe entlieht durch Verbindung des Boyleschen Gesetzes (s.d.) und des Gay-Lussacschen Gesetzes (s.d.) und gibt die Beziehung zwischen dem Drucke p, dem Volumen υ und der Temperatur t eines Gases (Zustandsgleichung). Es läßt sich für technische Zwecke am einfachsten in der schon von Sadi Carnot [1] angewendeten Form schreiben:

worin R konstant und von der Gasart abhängig, a konstant und von letzterer unabhängig, gewöhnlich gleich 273° gesetzt, so daß T= a + t = 273 + t, welche Größe jetzt die absolute Temperatur heißt. Andre Formen des Boyle-Gay-Lussacschen Gesetzes, wie

bei Vergleichung zweier Zustände p, υ, t und p, υ, t, oder

wenn der eine Zustand sich auf die Temperatur 0° C. bezieht, sind mehr in der Physik als in der Technik gebräuchlich. In 2., 3. ist α = 1/a. In der Regel wird 1. auf 1 kg Gas bezogen, womit υ das diesem entsprechende Volumen (das spezifische Volumen) bedeutet und für ein beliebiges Gasgewicht G vom Volumen V:

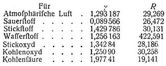
Nehmen wir dies im folgenden an und denken uns v in Kubikmetern, p in Kilogrammen pro Quadratmeter eingesetzt, so folgen aus 1. mit p = 10333 kg = 1 Atmosphäre, 0 oder 7 = 273° und den folgenden hierfür von Regnault[2] ermittelten γ = 1/υ die beigesetzten R:

Uebrigens hat man nach 1. für alle dem Boyle-Gay-Lussacschen Gesetze folgenden Gase bei gleichen p, T

wonach sich die R derselben aus demjenigen irgend eines von ihnen berechnen lassen, wenn die γ, γ' bei gleichen p, T bekannt sind. Ist das Gas vom Gewichte G ein Gemisch zweier Gase der Gewichte G₁, G₂, so hat man in 1., 4. auf Grund des Daltonschen Gesetzes (s.d.):

Für ein Gemisch beliebig vieler Gase wäre [7], S. 138:

worin die Summe rechts sich auf alle Einzelgase bezieht.

Genau genommen ist R in 1. und damit auch in 4. nur dann konstant, wenn allein Gaszustände an Orten von gleicher Acceleration g des freien Falls verglichen werden; vorgehende Zahlen beziehen sich auf Paris etwa 60 m überm Niveau des Meeres, wo g = 9,8096 m. Für manche Zwecke, z.B. für barometrische Höhenmessungen, genügt die Annahme eines konstanten R nicht. Es ist nun in 1., 4. genauer:

mit konstantem C, speziell für atmosphärische Luft C = 287,114 [7], S. 144, so daß man anstatt 1. und 4. auch schreiben kann:

unter M die Masse des Gases verbanden., Beim barometrischen Höhenmessen pflegt allerdings noch die Feuchtigkeit der Atmosphäre in angenäherter Weise berücksichtigt zu werden, indem man in 1., 4. setzt:

worin f den Beitrag des in der Luft befindlichen Wasserdampfes zum Drucke p, und ε eine Verhältniszahl bedeutet, die gewöhnlich 3/8 angenommen wird.

Das Boyle-Gay-Lussacsche Gesetz ist selbstverständlich denselben Beschränkungen unterworfen wie das Boylesche Gesetz und das Gay-Lussacsche Gesetz. Außer den für diese einzeln bestehenden Prüfungsmethoden ergibt sich eine weitere daraus, daß unter Voraussetzung beider Gesetze der Spannungskoeffizient gleich dem Ausdehnungskoeffizienten ist (= α = 1/a = 1/273, s. Spannungskoeffizient). Die kinetische Gastheorie (s. Gase) gestattet, das Gesetz mathematisch[244] abzuleiten [4], II, S. 25, [6], S. 128, [7], S. 237. Auf Grund aller Versuche und der kinetischen Gastheorie pflegt man anzunehmen, daß das Boyle-Gay-Lussacsche Gesetz einem Grenzzustände, dem idealen Gaszustande, entspricht, der von keinem wirklichen Gase erreicht wird, dem sich aber die letzteren um so mehr nähern, je weiter sie sich von ihrem Kondensationspunkte entfernen, je schwerer sie also von dem augenblicklichen Zustande aus kondensierbar sind. Das Boyle-Gay-Lussacsche Gesetz gilt also auch in der Technik nur für eine kleine Anzahl gasförmiger Körper, zu denen vor allem die atmosphärische Luft, sodann Wasserstoff, Sauerstoff, Stickstoff Kohlenoxyd und Stickoxyd, aber schon die Kohlensäure nicht ohne weiteres gehören. Im übrigen haben verallgemeinerte Beziehungen (s. Gase) oder die Formeln für gesättigte und überhitzte Dämpfe einzutreten (s. Dampf, gesättigter und überhitzter).

Literatur: [1] Carnot, Réflexions sur la puissance motrice du feu, Paris 1824, p. 67, 75. – [2] Regnault, Relation des expériences etc., Paris 1847 (zugleich Bd. 21 der Mém. de l'Acad. des sciences), p. 142. – [3] Grashof, Theoretische Maschinenlehre, I, Leipzig 1875, S. 100. – [4] Clausius, Die mechanische Wärmetheorie, I, Braunschweig 1887, S. 42; II, Braunschweig 1889–91, S. 25. – [5] Zeuner, Technische Thermodynamik, I, Leipzig 1900, S. 91. – [6] Weinstein, Thermodynamik und Kinetik der Körper, I, Braunschweig 1901, S. 122. – [7] Weyrauch, Grundriß der Wärmetheorie, I, Leipzig 1905, S. 124. – Weitere Literatur s. Boylesches Gesetz, Gay-Lussacsches Gesetz.

Weyrauch.