Momentmechanismus

Momentmechanismus, ein Mechanismus, bei dem vermöge seiner Gliederverbindung nur eine unendlich kleine gegenseitige Bewegung der Glieder stattfindet, bei dem also nur eine momentane Bewegung möglich ist.

Die Anwendung der Kinematik (s.d.) auf die Fachwerkträger hat zu der Betrachtung der Momentmechanismen geführt; denn wenn die als gelenkig angesehene Stabverbindung eines im allgemeinen starren Fachwerkträgers in der besonderen Art auftritt, daß diese Stabverbindung eine unendlich kleine Bewegung zuläßt, so ist der Fachwerkträger nicht statisch bestimmt und unbrauchbar.

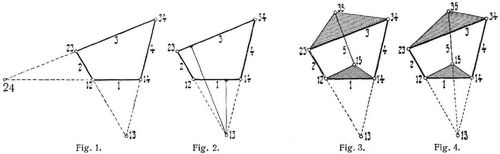
Betrachten wir z.B. den in Fig. 1 gezeichneten, viergliedrigen, zwangläufigen Mechanismus, dessen vier Glieder 1, 2, 3, 4 durch die vier Gelenke 12, 23, 34, 14 verbunden sind, so bewegen sich die Punkte des Gliedes 3 in bezug auf das Glied 1 in bestimmten Bahnkurven, und umgekehrt, und das gleiche gilt von den beiden Gliedern 2, 4. Eine unendlich kleine Bewegung des Gliedes 3 gegen das Glied 1 sowie des Gliedes 1 gegen das Glied 3 kann als eine unendlich kleine Drehung um den momentanen Pol 13 angesehen werden, der sich als Schnittpunkt der Geraden 12–23, 14–34 ergibt. Ebenso kann eine unendlich kleine Bewegung des Gliedes 4 gegen das Glied 2 sowie des Gliedes 2 gegen das Glied 4 als eine unendlich kleine Drehung um den momentanen Pol 24 angesehen werden, der sich als Schnittpunkt der Geraden 12–14, 23–34 ergibt.

Verbinden wir in Fig. 2 die beiden Glieder 1, 3 dieses Mechanismus in dem Pol 13 durch ein Gelenk, so kann dieser Mechanismus nur eine unendlich kleine Bewegung vollziehen und derselbe ist demnach ein Momentmechanismus. Ebenso können wir auch die Glieder 2, 4 in dem Pol 24 noch durch ein Gelenk verbinden, ohne die unendlich kleine Bewegung zu hemmen.

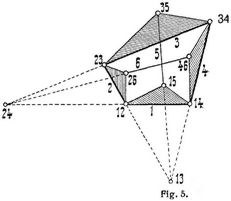
Werden in Fig. 3 die Glieder 1, 3 des in Fig. 1 betrachteten, zwangläufigen Mechanismus in beliebigen Punkten 15, 35 durch ein Glied 5 gelenkig verbunden, so wird dadurch der Mechanismus im allgemeinen unbeweglich, und wir erhalten also eine starre Gliederverbindung. Wenn aber in Fig. 4 die Punkte 15, 35 mit dem Punkt 13 in einer Geraden liegen, so ist eine unendlich kleine Bewegung des Mechanismus möglich, und derselbe ist demnach ein Momentmechanismus. Ebenso können wir in diesem Momentmechanismus in Fig. 5 auch die Glieder 2, 4[479] durch ein Glied 6 in den Punkten 26, 46 gelenkig verbinden, die mit dem Punkt 24 in einer Geraden liegen; und ferner können wir beliebig viele solche Glieder 5, 6 einfügen, ohne die unendlich kleine Bewegung zu hemmen. Diese unendlich kleine Bewegung vollzieht sich während eines Zeitelementes, wenn aber insbesondere der Punkt 15 ein Krümmungsmittelpunkt der von dem Punkt 35 gegen das Glied 1 beschriebenen Bahnkurve in dem aus den vier Gliedern 1, 2, 3, 4 bestehenden, zwangläufigen Mechanismus ist, und das Analoge von den Punkten 26, 46 gilt, dann vollzieht der Momentmechanismus eine unendlich kleine Bewegung während zweier Zeitelemente, d.h. alle sich bewegenden Punkte durchschreiten zwei benachbarte Elemente ihrer Bahnen.

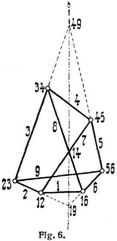
In Fig. 6 ist beispielsweise noch ein neungliedriger Momentmechanismus gezeichnet, bei welchem die Bedingung erfüllt sein muß, daß die sechs Gelenkpunkte 12, 23, 34, 45, 56, 16 auf einem Kegelschnitt liegen. Demzufolge müssen nach dem Pascalschen Theorem (s.d.) z.B. die drei Schnittpunkte 19, 49, 14 der Geradenpaare 2, 6 und 3, 5 sowie 7, 8 sich in einer Geraden befinden, und umgekehrt. Denn in dem aus der Folge der sechs Seiten 2, 3, 8, 6, 5, 7 gebildeten Sechseck schneiden sich die Gegenseitenpaare 2, 6 und 3, 5 sowie 8, 7 bezw. in den auf einer Geraden liegenden Punkten 19, 49, 1/4 [2].

Literatur: [1] Burmester, L., Ueber die momentane Bewegung der ebenen Mechanismen, Technische Blätter, Prag 1890, 22, Jahrg., S. 1 u. 73. – [2] Müller-Breslau, Die graphische Statik der Baukonstruktionen, Leipzig 1887, Bd. 1, S. 208; Föppl, A., Vorlesungen über technische Mechanik, Bd. 2, Graphische Statik, 2. Aufl., Leipzig 1903, S. 228.

Burmester.