Rückwärtseinschneiden

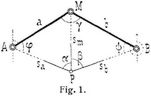
Rückwärtseinschneiden (Pothenotsche, besser Snelliussche Aufgabe, [1], [2]) benimmt die Lage eines Punktes P (Fig. 1) in bezug auf drei gegebene Punkte A, M, B durch die in P gemessenen oder aufgezeichneten Winkel a, ß. Die gegenseitige Lage der Punkte A, M, B kann ausgedrückt sein: 1. durch die Seiten a, b und den eingeschlossenen Winkel γ; 2. durch die rechtwinkligen Koordinaten y_ax_a, y_mx_m, y_bx_b; da aus den Koordinaten die Werte a, b und γ abgeleitet werden können, schließt dieser Fall den ersten ein; 3. graphisch in einer Karte, z.B. dem Meßtischblatt. Im Falle 1 ist die Aufgabe gelöst, sobald die unbekannten Stücke des Vierecks A M B P, also φ, ψ und damit die Winkel bei M sowie die Seiten s_a, s_m, s_b berechnet sind; im Falle 2 sind mit Hilfe dieser Werte noch die Koordinaten yx von P abzuleiten; im Falle 3 erfolgt die Lösung durch Konstruktion.

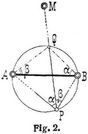
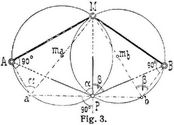
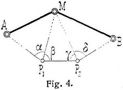
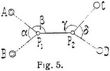
A. Die trigonometrische Lösung. Die für logarithmische Rechnung gebräuchlichste und auch wohl bequemste Lösung (Lambert, Burckhardt, Bessel [2]) ist die folgende: 1. Ableitung der Richtungswinkel und Längen der Linien a, b und des Winkels y aus den gegebenen Koordinaten (s. Koordinaten, geodätische). 2. Berechnung der unbekannten Winkel φ und ψ aus φ = ¹/₂ (φ + ψ) + ¹/₂ (φ – ψ); ψ = ¹/₂ (φ + ψ) – ¹/₂ (φ – ψ), worin φ + ψ = 360° – (γ + α + ß) und tg ¹/₂ (φ – ψ) = cotg (45° + μ) tg ¹/₂ (φ + ψ) und Hilfswinkel, μ zu bestimmen ist aus tg μ = a sin ß : b sin α = sin ψ : sin φ (Probe). 3. Damit lassen sich die übrigen Winkel und Seiten und daraus wieder die Richtungswinkel und Koordinatenunterschiede berechnen. – Eine andre Lösung ist an Fig. 2 erläutert. Der durch einen um A B P beschriebenen Kreis auf der Richtung MP abgeschnittene Punkt Q, der Collinssche Hilfspunkt, ist seiner Lage nach im Dreieck ABO bestimmt durch die Winkel a und ß, wie aus der Figur unmittelbar ersichtlich ist. Danach lassen sich alle Seiten, Richtungswinkel und Koordinatenunterschiede berechnen oder auch konstruieren. Dieses Verfahren ist zurzeit praktisch angewendet in [7]; s. dazu auch [5]. – Weitere Lösungen (Fig. 3) gehen von den durch A M P und B M P beschriebenen Bestimmungskreisen mit den Peripheriewinkeln α und ß aus, wobei auch wie von Snellius die Kreismittelpunkte m_a und m_b eingeführt werden können. Die in diesen Bestimmungskreisen bestehenden Beziehungen ergeben sich unmittelbar aus der Figur. Der gesuchte Punkt P ist die Projektion des Mittelpunktes M auf die Sekante ab, deren Endpunkte a, b bestimmt sind durch die bei A und B rechtwinkligen Dreiecke M A a und M B b. Dieser Rechnungsgang ist für die Rechnung mit der Rechenmaschine ausgenutzt worden, insbesondere bei der Leipziger Stadtvermessung [3], ferner s. [4]. – Andre Lösungen sowie die betreffenden Literaturangaben s. [1] und [2]. Näheres über die Anordnung der Rechnung in verschiedenen Fällen in bezug auf Lage der Punkte, die Ausführung der Zahlenrechnung und Rechenformulare s. [1], Jordans Handbuch und [3]–[7].[528] Die Aufgabe läßt mehrfache Erweiterungen zu; nach Fig. 4 können z.B. zwei oder mehr Punkte P₁ P₂ ... gegen A, M, B bestimmt werden, sobald die Richtungen von allen Punkten nach M vorliegen. Eine andre Erweiterung drückt Fig. 5 aus (Mareks Aufgabe), wozu sich besonders die Lösung mit dem Collinsschen Hilfspunkte eignet. Weiteres s. [1], [2]. Vgl. a. Hansens Aufgabe und Triangulierung.

B. Graphische Lösung. Wird das durch α, ß gegebene Strahlenbüschel (Fig. 1) so in das System der gegebenen Punkte eingepaßt, daß jeder Strahl durch den zugehörigen Punkt A, M, B geht, so ist die Lage von P bestimmt. Eine einfache Anwendung dieses Satzes ist das Aufzeichnen der Richtungen auf Pauspapier und ihr Orientieren nach den gegebenen Punkten. Dasselbe Prinzip findet Verwendung beim Einschneidetransporteur (s.d.) oder Standpeiler. Dieses Instrument ist eine Gradscheibe, um die drei oder mehr Lineale zentrisch dreh- und feststellbar sind; nach Einstellung der Lineale wird verfahren wie bei der Aufzeichnung auf Pauspapier. Demselben Zweck dient der sogenannte Goniograph (s.d.). Auf der Bestimmung des Punktes P als Schnittpunkt der Bestimmungskreise (vgl. Fig. 3) durch Konstruktion der Kreise nach Einstellung der Peripheriewinkel beruht Bauernfeinds Einschneidezirkel (s. Bd. 3, S. 245). Eine direkte Lösung folgt aus Fig. 2. Der Meßtisch wird mit A B über P nach B orientiert und ß wird angetragen. Danach wird er mit BA nach A orientiert und α wird angetragen. Hierdurch erhält man Q. Durch Orientierung des Tisches mit QM nach M ergibt sich P. – Größere Bedeutung als die direkte und die mechanische Lösung hat für die Meßtischpraxis die indirekte Lösung. Der Meßtisch wird nach Augenmaß oder besser mit Hilfe einer Orientierbussole genähert orientiert, und die Richtungslinien werden mit der Kippregel gezogen. War die Orientierung nicht genau richtig, so ergibt sich statt des Schnittpunktes ein Schnittdreieck, das fehlerzeigende Dreieck, dessen Form von der gegenseitigen Lage der vier Punkte und dem Fehler der Orientierung abhängt. Ueber die Lage des Punktes P zum Fehlerdreieck handelt Lehmanns Satz. Vgl. hierüber [8], [9] sowie [1], Jordan, Bauernfeind, Hartner-Wastler. Werden die Richtungslinien bei einer zweiten Orientierung konstruiert, so erhält man durch die gleichnamigen Richtungsschnitte drei den Eckpunkten des ersten Fehlerdreiecks entsprechende Punkte. Die Verbindungslinien der einander entsprechen den Punkte schneiden sich in dem gesuchten Punkte und bestimmen diesen. – Wie aus Fig. 3 ohne weiteres folgt, versagt die Lösung rechnerisch und graphisch, wenn die vier Punkte A, M, B, P auf einem Kreise liegen, d h. wenn die beiden Bestimmungskreise, deren Schnitt den Punktort anzeigt, zusammenfallen, wenn also ∞ viele Punkte der Bedingung entsprechen. Beim rechnerischen Verfahren nach Fig. 1 werden hierbei φ + ψ = 180°, μ = 45° und φ – ψ unbestimmt; entsprechend bleiben in Fig. 2 die Richtung MQ und in Fig. 3 a und b unbestimmt. Liegt P nahe an dem Kreis durch A, M, B, den man den gefährlichen Kreis nennt, so ist die Punktbestimmung unsicher. Solche Verhältnisse müssen also vermieden werden. Günstig ist, wenn das Viereck A M B P bei M oder P eine einspringende Ecke hat, und wenn sich zwei Richtungen in P nahezu rechtwinklig schneiden. Weiteres über die günstigste Auswahl der Bestimmungspunkte in [1], [6], [7]. Ueber die Genauigkeit des einfachen Rückwärtseinschneidens s. Jordans Handbuch und die dort angegebene Literatur. Ueber die Anwendung des Rückwärtseinschneidens mit überzähligen Winkeln oder Richtungen nach mehr als drei gegebenen Punkten s. Triangulierung.

Literatur: [1] Die bei Geodäsie unter [4]–[8] genannten Lehrbücher. – [2] Zeitschr. für Vermessungsw. 1892, S. 296–302, und Jordans Handbuch, Bd. 2, S. 351, sowie auch Hammer, Zeitschr. für Vermessungsw. 1895, S. 598. – [3] Höckner, Einschaltung von Punkten in ein durch Koordinaten gegebenes trigonometrisches Netz mit ausgiebiger Verwendung der Rechenmaschine, Leipzig 1891. – [4] Runge, Zeitschr. für Vermessungsw. 1894, S. 204; Soßna, ebend. 1896, S. 269. – [5] Koll, Geodätische Rechnungen mittels der Rechenmaschine, Halle a. S. 1903. – [6] Gauß, F.G., Die trigonometrischen und polygonometrischen Rechnungen, 3. Aufl., Halle a. S. 1906. – [7] IX. Anweisung für die trigonometrischen und polygonometrischen Arbeiten, Berlin, 1. Aufl. 1881, 2. Aufl. 1894, 3. Aufl. 1903 (vgl. auch die anderen bei Kataster genannten amtlichen Vermessungsanweisungen). – [8] Lehmann, Anleitung zum vorteilhaften und zweckmäßigen Gebrauch des Meßtisches (5. Aufl. 1843, S. 55, herausgeg. von Becker u. Fischer), Dresden-Leipzig. – [9] Vorschrift für die topograph. Abteilung der Landesaufnahme, Heft 1, Berlin 1898.

(† Reinhertz) Hillmer.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.

Fig. 5.