Hansens Aufgabe

Hansens Aufgabe, die Aufgabe der unzugänglichen Entfernung oder der zwei unzugänglichen Punkte oder der zwei Punktpaare genannt, behandelt die Bestimmung der gegenseitigen Lage von vier Punkten, wenn auf zwei Punkten die Richtungen (Winkel) nach den zwei andern Punkten gemessen und für die ersteren oder die letzteren die Entfernung oder die Koordinaten bekannt sind.

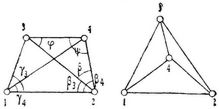
Wenn z.B. in der Figur irgendeine der Seiten (etwa 1–2 = s) und an ihren Endpunkten in 1 und 2 die Winkel nach 3 und 4 (β, β₃, β₄, γ₃, γ₄) gemessen sind, so können alle übrigen Stücke der Figur berechnet werden. Es ist

worin φ und ψ bestimmt werden aus ¹/₂ (φ + ψ) = 90° – ¹/₂β, und tg ¹/₂ (φ – ψ) = cotg (45° + μ) tg ¹/₂ (φ + ψ) und der Hilfswinkel μ aus

In diesem Fall nennt man 1–2 = s die Standlinie und 3–4 die unzugängliche Entfernung. Sind z.B. die Punkte 3, 4 durch ihre Koordinaten (und damit ihre Entfernung) gegeben, so können durch die auf 1 und 2 gemessenen Winkel auf dem gleichen Wege die Koordinaten dieser Punkte berechnet werden. Bei der Lösung der Aufgabe kommen je nach der Lage der gegebenen Stücke verschiedene Fälle in Betracht. Näheres hierüber sowie über zweckmäßige Anordnung der Zahlenrechnung s. [1]–[3].

Die Aufgabe ist nach Hänsen wegen der in [4] gegebenen Lösung benannt, obwohl dieselbe schon vorher lange bekannt und mehrfach gelöst war, so z.B. schon 1790 von van Swinden [5] und manchen andern [6], [7]. – Die Aufgabe findet Anwendung bei der trigonometrischen Punktbestimmung, und zwar zur Ableitung der Koordinaten von zwei Punkten durch Winkelmessung auf diesen Punkten nach zwei durch Koordinaten gegebenen Punkten, und bei der Bestimmung der sogenannten »unzugänglichen« Entfernung, besonders beim Zentrieren von trigonometrischen Nebenpunkten; vgl. [8].

Literatur: [1] Die beim Art. Geodäsie genannten Lehrbücher, besonders Jordan, Handbuch der Vermessungskunde, Bd. 2; Bauernfeind, Elemente der Vermessungskunde, Bd. 2, Vogler, Lehrbuch der praktischen Geometrie, Bd. 1; Botin, Die Landmessung, und [2] Gauß, F.G., Die trigonom. und polygonom. Rechnungen der Feldmeßkunst, Berlin 1893. – [3] Hammer, Lehrbuch der ebenen und sphärischen Trigonometrie, Stuttgart 1897. – [4] Astronom. Nachr., Nr. 419 (Bd. 18), S. 165. – [5] van Swinden, J.H., Grondbeginsels der Meetkunde, Amsterdam 1790, S. 357, over een tweede belangrijk Geval in de Praktijk. – [6] Meinert, Anfangsgründe der Feldmeßkunst, Halle 1794, S. 204. – [7] Astronom. Nachr., Bd. 3, Nr. 62 (Jahrg. 1825), S. 233, Lösung von Gerling; ebend. Bd. 7, Nr. 157 (Jahrg. 1829), S. 239, Lösung von Hartmann. – [8] Anw. 9 für die trigonom. und polygonom. Arbeiten u.s.w., Berlin 1893.

Reinhertz.