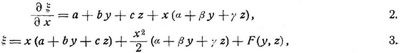Saint-Venants Problem

Saint-Venants Problem, Behandlung der Biegung eines prismatischen Stabes auf Grund der allgemeinen Elastizitätsgleichungen isotroper fester Körper (Bd. 3, S. 382) unter eigentümlichen beschränkenden Voraussetzungen [1], [2].

Da die technische Biegungstheorie von unbewiesenen Annahmen ausgeht (Bd. 1, S. 792), die Integration der allgemeinen Elastizitätsgleichungen (Bd. 3, S. 391) für beliebige äußere Kräfte (s.d.) aber nicht gelang, so faßte de Saint-Venant folgenden Fall ins Auge (vgl. die Figur):

Ein gerader prismatischer Stab werde in einem Querschnitt so gehalten (oder das Koordinatensystem bewege sich so mit dem Stab), daß der Achspunkt jenes Querschnitts (Ursprung der Koordinaten) keine Verrückungen erleidet, die Punkte eines Linienelements durch den Achspunkt sich nicht aus der Richtung desselben (y-Achse) entfernen, und die Punkte eines Flächenelements durch den Achspunkt nicht aus dessen Ebene (y z-Ebene) treten, Bedingungen, welche eben ausreichen, jede Bewegung eines starren Körpers (s. Kohäsion) hinsichtlich des erwähnten Koordinatensystems unmöglich zu machen. Der elastische Stab aber kann Formänderungen erleiden, wobei ein Körperpunkt, welcher anfänglich bei x, y, z lag, im allgemeinen Wege ξ, η, ζ in den Richtungen x, y, z zurücklegt. Nur bei dem Punkt x = y = z = 0 hat man nach obigen Voraussetzungen:

Die ξ, η, ζ, sollen kleine Größen gegen die x, y, z sein. Vom Eigengewicht wie von Temperaturänderungen des Stabs wird abgesehen. Aeußere Kräfte sind nur auf die Endquerschnitte, nicht auf die Mantelfläche zugelassen. Saint-Venant traf für diese äußeren Kräfte keine Wahl, sondern nahm sie behufs Ermöglichung einer Lösung versuchsweise so an (vgl. [4], franz. Ausg., S. 144): A. daß die parallel der Stabachse gedachten prismatischen Fasern keine Kräfte senkrecht zur Stabachse aufeinander ausüben (bei den Bd. 3, S. 389 eingeführten Bezeichnungen Yy = Zz = 0, Yz = Zy = 0); B. daß die Dehnungen in den Längsrichtungen dieser Fasern (die Werte ∂ξ/∂x, vgl. Bd. 2, S. 692; Bd. 3, S. 390) nach der Quere nur linear veränderlich sind. Unter diesen Voraussetzungen wird bei konstantem Elastizitätsmodul E (s.d. und Elastizitätsgesetz) die Normalspannung für die Querschnittselemente ebenfalls nach der Quere nur linear veränderlich: Xx = E ∂ξ/∂x. Bekanntlich macht auch die technische Biegungstheorie jene Annahmen A., B. (abgesehen von der jetzigen Berücksichtigung des Einflusses der Schubkräfte auf die Biegung, Bd. 1, S. 792, 793), wobei sie bezüglich B. auf der spezielleren Annahme eben bleibender Querschnitte fußt. Die Integration der Differentialgleichungen für die angegebenen Verhältnisse führte zu gewisser, von der Querschnittsform abhängiger Verteilung der äußeren Kräfte auf die Endquerschnitte (nach gleichem Gesetze wie für die Beanspruchungen der inneren Querschnitte), so daß für diese Verteilung und die Voraussetzungen der Ableitung die Annahmen A., B. bewiesen erscheinen, und die Querschnitte nach der Biegung schwach gekrümmt wären. Die fragliche Verteilung der äußeren Kräfte auf die Querschnitte ist nun zwar nicht die in der Praxis übliche, doch nahm man an, daß hierdurch nur in der Nähe der Angriffspunkte erhebliche Abweichungen entstehen können, so daß die Voraussetzungen A., B. für technische Zwecke im allgemeinen genügend seien ([4], franz. Ausg., S. 169, 174, [8], S. 141). Dabei ist zu beachten, daß sich ein in der gebräuchlichen Weise beliebig belasteter Stab in Abschnitte mit nur in den Endquerschnitten angreifenden äußeren Kräften zerlegen läßt, während ein Einfluß der Verteilung dieser Kräfte auf ihre Querschnitte in einiger Entfernung von diesen nicht hervortritt.

Clebsch [4] behandelte das de Saint-Venantsche Problem zugleich mit der Torsion prismatischer Stäbe, bei welcher ebenfalls nur äußere Kräfte auf die Endquerschnitte vorausgesetzt werden (vgl. Torsionselastizität). Er erhielt u.a. im Einklänge mit den getrennten Untersuchungen beider Fälle durch Saint-Venant ([4], S. 78, [6], S. 223):

worin a, b, c, α, ß, γ von x, y, z unabhängig, F (y, z) eine vom Querschnitt abhängige Funktion von y, z, so daß auch die durch 3. bestimmte schließliche Form der anfänglich ebenen Querschnitte vom Querschnitt mitabhängt. Wenn die äußeren Kräfte symmetrisch zu einer Symmetrieebene des Stabes angreifen, liegen selbstverständlich auch gleiche ξ symmetrisch zur letzteren. Weitere Darstellungen des Saint-Venantschen Problems s. [5], [6], [8]–[12]. Ueber unendlich dünne Stäbe s. [3], [4], S. 190.

[557] Pochhammer [7] untersuchte auf Grund der allgemeinen Elastizitätsgleichungen die Biegung isotroper Stäbe von endlichem (auch innerhalb gewisser Grenzen variabelm) Querschnitt, auf deren ganze Oberfläche beliebige äußere Kräfte wirken. Die ξ, η, ζ werden klein gegen die x, y, z vorausgesetzt; die Behandlung läßt, wie die Integration durch unendliche Reihen, beliebige Annäherung zu. Pochhammer sieht die größte Querdimension c als klein gegen die Stablänge l an, also (c/l)ⁿ als kleine Größe n-ter Ordnung gegen 1, klassifiziert alle Größen nach den Werten, welche sie höchstens erreichen können, zerlegt die Formänderungen nach diesen Größen in Bestandteile, und kann so je nach der Anzahl berücksichtigter Glieder beliebige Grade der Annäherung erreichen [7], S. 37. Es ergibt sich, daß die Grundhypothesen der Navierschen Biegungstheorie, wonach die der Stabachse parallelen Fasern keine Querkräfte aufeinander ausüben und die Querschnitte auch nach der Biegung Ebenen bilden (Bd. 1, S. 792), für gerade Stäbe beliebigen Querschnitts in erster Annäherung zutreffen [4], S. VIII, 59, 61. Das Ebenbleiben der Querschnitte fanden u.a. Bauschinger und Considère bei Versuchen mit Stahl fast vollkommen bestätigt (Zeitschr. d. Bayer. Arch.- u. Ing.-Ver. 1877, S. 87, bezw. Die Anwendung von Eisen und Stahl, Wien 1888, S. 38, 41) und Foeppl selbst für Granit und Sandstein annähernd zutreffend (Mitteil. aus dem mechan.-techn. Laboratorium zu München, 1896, 24. Heft, S. 4). Trotzdem genügen jene Annahmen auch für technische Zwecke nicht allgemein, wie die Notwendigkeit der Berücksichtigung des Einflusses der Schubkräfte auf die Biegung beweist (vgl. Bd. 1, S. 797; Bd. 3, S. 394 u.s.w.). Ueber die Biegung einfach gekrümmter Stäbe s. [8], S. 144, 169.

Literatur: [1] Barré de Saint-Venant, Mémoire sur la flexion des prismes élastiques, sur les glissements qui l'accompagnent lorsqu'elle ne s'opère pas uniformément ou en arc de cercle, et sur la forme courbe affecté alors par leurs sections transversales primitivement planes, Comptes rendus etc. 1854, XXXIX, S. 1027 (Auszug von [2], s.a. C.R. 1855, XLI, S. 143). – [2] de Saint-Venant, Mémoire sur la flexion des prismes (ganzer Titel wie [1]), Journal des mathématiques pures et appliquées de Liouville 1856, I, S. 89. – [3] Kirchhoff, Ueber das Gleichgewicht und die Bewegung eines unendlich dünnen elastischen Stabes, Journal für reine u. angew. Mathematik 1859, S. 285 (s.a. Kirchhoff, Mechanik, Leipzig 1877, S. 407). 150; [4] Clebsch, Theorie der Elastizität fester Körper, Leipzig 1862, S. 70 (franz. Ausg. mit Noten von Saint-Venant, Paris 1883, S. 137). – [5] Winkler, Die Lehre von der Elastizität und Fertigkeit, Prag 1867, S. 235. – [6] Grashof, Theorie der Elastizität und Fertigkeit, Berlin 1878, S. 217. – [7] Pochhammer, Untersuchungen über das Gleichgewicht des elastischen Stabes, Kiel 1879. – [8] Castigliano, Théorie de l'équilibre des systèmes élastiques et ses applications, Turin 1880, S. 102 (deutsch von Hauff, Wien 1886, S. 95). – [9] Ibbeston, An elementary treatise on the mathematical theory of perfectly elastic solids, London 1887, S 386. – [10] Poincaré, Leçons sur la théorie de l'élasticité, Paris 1892, S. 166. – [11] Foeppl, Festigkeitslehre, Leipzig 1900, S. 429. – [12] Love, Lehrbuch der Elastizität, deutsch von Timpe, Leipzig und Berlin 1900, S. 379.

Weyrauch.