Schwere

Schwere (Schwerkraft) ist die Resultante aus der Anziehungskraft der Erde und der Zentrifugalkraft infolge der Erddrehung. Ihre Wirkung auf einen relativ zur Erde ruhenden Körper heißt dessen Gewicht und kann für nicht zu ausgedehnte Körper im Massenmittelpunkt (Schwerpunkt) angreifend gedacht werden.

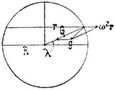
Wäre die Erde eine konzentrisch geschichtete Kugel vom Radius R, so wäre auf der Oberfläche die Anziehung G konstant. Die Zentrifugalkraft ist ω² r (ω die Winkelgeschwindigkeit der Erddrehung). Die Resultante g beider wird

Setzt man hierin r = R cos λ, berücksichtigt man ferner, daß die Schwere g_a am Aequator g_a = G – ω² R² ist und entwickelt man die Wurzel unter Vernachlässigung der vierten und höheren Potenzen von ω, so ergibt sich: g = g_a (1 + ω² R/g_a sin ²λ). Die Abnahme der Schwere g_h – g mit der Höhe h erfolgt unter obiger Voraussetzung nach der Formel g_h – g = – g_a 2 h/R + h ω² sin ²λ. Wegen des zweiten Gliedes h ω² sin ²λ. ist dieselbe am Aequator (λ = 0) größer als an den Polen. Die Niveauflächen der Schwere sind unter diesen Annahmen durch die Gleichung g_a R²/R + h + ω²/2 (R + h)² sin²λ = const. gegeben. Für Werte von h, welche klein gegen r sind, stellen die Flächen an den Polen abgeplattete Ellipsoide dar. In Wirklichkeit liegen die Dinge verwickelter; die Erde ist keine Kugel, sondern annähernd eine Niveaufläche der Schwere, ein abgeplattetes Ellipsoid. Trotzdem besteht ein ähnlicher Zusammenhang zwischen der Schwere g₀ im Meeresniveau und der geographischen Breite φ (Winkel zwischen Schwererichtung und Aequatorebene). Dieser ist nach Helmert auf Grund vieler Pendelbeobachtungen empirisch ermittelt worden zu g₀ = 9,78035 (1 + 0,005310 sin φ). Für die Höhenabnahme ergibt sich unter Voraussetzung kleiner Höhen g_h – g₀ = – 0,0003086 h. Clairaut hat schon 1743 gezeigt, daß unter der Annahme, daß die Erdoberfläche Niveaufläche der Schwere ist, ein solches Gesetz g₀ = g_a (1 + β sin φ) gelten muß und daß der Koeffizient β in folgendem Zusammenhang mit der Abplattung a – b/a der Erdoberfläche steht: a – b/a = ⁵/₂ (ω² a)/g_a – β (a äquatorialer, b polarer Erdhalbmesser). Aus Helmerts Formel wird die Abplattung 1 : 298,3. Die Helmertsche Formel gibt nur den normalen Teil der Schwere, der durch die Unregelmäßigkeiten der Massenverteilung an der Erdoberfläche nicht beeinflußt ist. Die Schwereanomalien gegenüber dieser Formel stellen sich bei der Beobachtung meist weit geringer heraus, als sie nach den sichtbaren Massen zu erwarten wären. Man erklärt das durch die Hypothese, daß den sichtbaren Massenanhäufungen (Kontinenten, Gebirgen) unterirdische Massendefekte entsprechen, die ihre anziehende Wirkung kompensieren (Isostasie der Erdrinde nach Pratt).

Die Formeln für die Schwere gelten strenge genommen nur für relative Ruhe gegenüber der Erde. Bei der Bewegung eines Punktes oder Körpers gegen die Erde müssen noch die sogenannten Coriolisschen Zusatzkräfte (vgl. relative Bewegung Bd. 1, S. 768) in Rücksicht gezogen werden.

Literatur: Clairaut, A.C., La théorie de la figure de la terre tirée des principes de l'hydrostatique, Paris 1743; Stockes, G., On the Variation of gravity at the earth, Cambridge Philos. Transactions Bd. VIII (1849); Helmert, F.R., Die math. und phys. Theorie der höheren Geodäsie, Bd. 2, Leipzig 1884; Pratt, J.H., A treatise on attractions London 1871; Helmert, F.R., Der normale Teil der Schwerkraft im Meeresniveau, Sitzungsber. d. Berl. Akad. 1901, S. 328.

Finsterwalder.