- Seilkurve
Seilkurve, in der graphischen Statik die Kurve, in welche ein Seilpolygon für parallele Kräfte (s. Parallelkräfte) übergeht, wenn die Belastung nicht aus Einzelkräften besteht, sondern stetig verteilt ist.
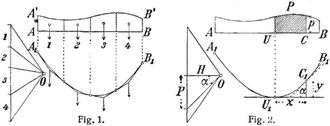
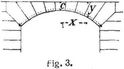
Um für eine gegebene verteilte Belastung die Seilkurve zu erhalten, teilt man (Fig. 1) die Belastungsfläche A B B' A' in eine beliebige Anzahl lotrechter Streifen, betrachtet die Inhalte dieser Flächenteile als Kräfte, die in den entsprechenden Schwerpunkten angreifen, und trägt sie in einem bestimmten Maßstab als lotrechte Kräfte auf (Fig. 1, links). Bei der Bestimmung der Schwerpunkte darf man die Flächenteile gewöhnlich als Trapeze ansehen (vgl. Schwerpunktsbestimmung). Nun zeichnet man das Seileck A1 B1 genau so, als ob es sich um Einzelkräfte handelte; dann sind die Seilseiten die Tangenten an die gesuchte Seilkurve, und zwar liegen die Berührungspunkte dieser Tangenten lotrecht unter den Trennungslinien der Flächenteile. – Die Richtigkeit dieses Verfahrens ergibt sich aus dem Satze, daß bei einem Seilecke die Mittelkraft einer Anzahl aufeinander folgender Kräfte durch den Schnittpunkt der einschließenden Seilseiten geht (vgl. a. Seilpolygon). Denn hier spielen die Tangenten der Seilkurve die Rolle der einschließenden Seilseiten; je zwei aufeinander folgende Tangenten müssen sich daher lotrecht unter dem Schwerpunkte des eingeschlossenen Belastungsteils schneiden. – Der Zusammenhang der Seilkurve A1 B1 mit der Belastungsfläche A B läßt sich in der Sprache der[67] höheren Mathematik wie folgt ausdrücken: Es seien (Fig. 2) U1 der tiefste und C1 ein beliebiger Punkt der Seilkurve, x und y seien deren Koordinaten. Dann wird nach der Theorie des Seilpolygons für parallele Kräfte (vgl. Parallelkräfte, Bd. 7, S. 31) die Größe P der zwischen U und C wirkenden Belastung gefunden, wenn man durch den Pol O des Kraftecks zwei Strahlen zieht, die zu den Tangenten in U1 und C1 parallel laufen. Daraus folgt tang α = d y/d x = P/H. Durch Differenzieren ergibt sich d2 y/d x = d P/H oder, wenn man d P durch p · d x ersetzt, d2 y/d x2 = p/H. – Nimmt man beispielsweise p konstant an, so findet man durch zweimalige Integration y = c + c1 x + p x2/2 H, d.h. die Seilkurve für gleichförmig verteilte Belastung ist eine Parabel mit lotrechter Achse. – Verlangt man, daß die Drucklinie (s.d.) eines oben wagrecht abgeglichenen Gewölbes mit der Gewölblinie zusammenfalle (Fig. 3), so setzt man p = γ y und findet hieraus
(Kettenlinie).
Literatur s. Graphische Statik.
Mörsch.
http://www.zeno.org/Lueger-1904.