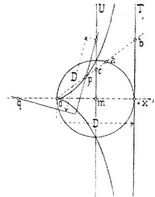
Cissoide

Cissoide

Cissoide. Durch einen beliebigen Punkt o eines Kreises ziehe man irgend einen Strahl, der den Kreis zum zweitenmal im Punkt a, diejenige Tangente des Kreises, deren Berührungspunkt o gegenüberliegt, im Punkt b schneiden möge. Trägt man in dem Strahl das Stück o p = a b ab, so ist p ein Punkt der durch den gegebenen Kreis (und den Punkt o auf ihm) bestimmten Cissoide. Man kann auch, wenn jener Strahl die durch den Kreismittelpunkt m zur Tangente T gezogene Parallele U in c schneidet, c p = a c machen.

Mechanische Erzeugung (nach Newton): Sei m o um sich selbst verlängert bis q. Man lasse einen Schenkel eines rechten Winkels um q sich drehen und zugleich denjenigen Punkt des andern Schenkels, der vom Scheitel um ein Stück gleich dem Durchmesser D des Kreises absteht, auf der Geraden U gleiten, dann wird der Mittelpunkt zwischen dem Scheitel des rechten Winkels und dem fraglichen Punkt des zweiten Schenkels die Cissoide beschreiben. Die Cissoide ist eine rationale Kurve dritter Ordnung und Klasse, die durch die unendlich fernen imaginären Kreispunkte geht; sie ist symmetrisch zu dem von o ausgehenden Durchmesser des gegebenen Kreises, hat T zur Asymptote und in o einen Rückkehrpunkt erster Art. Nimmt man o zum Ursprung, die Symmetrieachse zur x-Achse eines rechtwinkligen Koordinatensystems, so wird die Gleichung der Cissoide

x (x2 + y2) – Dy2 = 0,

oder in Polarkoordinaten r, φ

r = D · sinφ tgφ.

Darstellung in Parameterform:

x = D sin2φ, y = D sin2φ tgφ,

oder für x/y = ctgφ = t:

x = D/(1+t2), y = D/t(1+t2).


Literatur: Angaben über Tangente, Normale, Krümmung, Bogenlänge, Inhalt u.s.w. findet man in L.A. Sohncke, Sammlung von Aufgaben aus der Differential- und Integralrechnung,[468] 4. Aufl., Halle a. S. 1875/77, Teil 1, S. 177; Teil 2, S. 109; Schlömilch, O., Uebungsbuch zum Studium der höheren Analysis, 4. Aufl., Leipzig 1887 (an verschiedenen Stellen zerstreut); Loria, G., Spezielle algebraische und transzendente ebene Kurven, deutsche Ausgabe von Fr. Schütte, Leipzig 1902, S. 36, u.a. (s. Sachregister); dort auch weitere Literatur.

Mehmke.

Cissoide

http://www.zeno.org/Lueger-1904.

Игры ⚽ Нужна курсовая?
Synonyme:
, , ,


Schlagen Sie auch in anderen Wörterbüchern nach:

  • Cissoide — Cissoïde La cissoïde ou (courbe) cissoïdale de deux courbes (C1) et (C2) par rapport à un point fixe O est le lieu géométrique des points P tels que : où P1 est un point de (C1) et P2 un point de (C2), P1 et P2 étant alignés avec O. La… …   Wikipédia en Français

  • Cissoīde — (griech., »die Efeuähnliche«), eine ebene Kurve dritter Ordnung, die so erhalten wird: Über O A als Durchmesser (s. Abbildung) beschreibt man einen Kreis und zieht durch A die Senkrechte zu O A; ist dann R ein beliebiger Punkt auf dieser… …   Meyers Großes Konversations-Lexikon

  • cissóide — adj. 2 g. 1. Semelhante, na forma, à folha da hera. 2. Diz se de certa curva de 3.o grau que oferece o contorno de uma folha de hera, inventada pelo geômetra grego Déocles, para resolver o problema de duas médias proporcionais entre duas linhas… …   Dicionário da Língua Portuguesa

  • Cissoīde — (v. gr., Math.), eine krumme Linie des 3. Grades, deren Gleichung ist: x (y2 + x2) – ay2 = o. Wenn man einen Kreis vom Durchmesser a beschreibt, in demselben einen Durchmesser zieht, in dem einen Endpunkte desselben eine Berührende construirt,… …   Pierer's Universal-Lexikon

  • Cissoide — Cissoīde (grch.), krumme Linie dritter Ordnung [Abb. 356]; sie ist der geometr. Ort der Fußpunkte der vom Scheitel einer Parabel auf ihre Tangenten gefällten Lote …   Kleines Konversations-Lexikon

  • Cissoide — Cissoide, eine von dem Griechen Diokles erfundene krumme Linie zur Auflösung der Aufgabe, 2 mittlere Proportionalen zwischen 2 gegebenen geraden Linien zu finden. Sie besteht aus 2 vollkommen gleichen Zweigen, rechts und links von der Axe eines… …   Herders Conversations-Lexikon

  • cissoide — |ói| adj. 2 g. 1. Semelhante, na forma, à folha da hera. 2. Diz se de certa curva de 3.o grau que oferece o contorno de uma folha de hera, inventada pelo geômetra grego Déocles, para resolver o problema de duas médias proporcionais entre duas… …   Dicionário da Língua Portuguesa

  • Cissoïde — La cissoïde ou (courbe) cissoïdale de deux courbes (C1) et (C2) par rapport à un point fixe O est le lieu géométrique des points P tels que : où P1 est un point de (C1) et P2 un point de (C2), P1 et P2 étant alignés avec O. La cissoïde peut… …   Wikipédia en Français

  • cissoïde — (si sso ï d ) s. f. Terme de géométrie. Courbe du 3e degré offrant le contour d une feuille de lierre. •   Bien qu ils aient imaginé la cissoïde, DESC. Géom. 2. ÉTYMOLOGIE    En grec, lierre et forme …   Dictionnaire de la Langue Française d'Émile Littré

  • Cissoïde de Dioclès — avec son cercle et sa droite génératrice La cissoïde de Dioclès est une courbe construite par Dioclès au IIe siècle av. J.‑C. dans le but de résoudre graphiquement le problème de la duplication du cube. Elle fut étudiée plus… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”