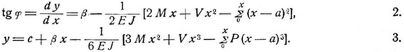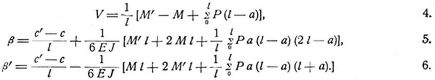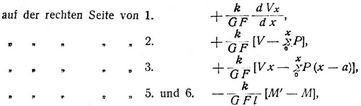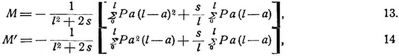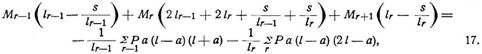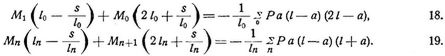- Elastische Linie
Elastische Linie wird bei gebogenen Stäben die Stabachse nach der Biegung genannt. Ihre Kenntnis ist in der Ingenieurmechanik besonders bei Ableitung von Einsenkungen (s.d.) und solcher sonstiger Größen nötig, die durch[376] statische Beziehungen allein nicht bestimmbar sind, z.B. der Stützenmomente durchlaufender (kontinuierlicher) und eingespannter einfacher Balken (s.d.). Für horizontale Balken (tg φ in Fig. 1 muß gegen 1 zu vernachlässigen sein, vgl. Bd. 1, S. 504) ist unter den gewöhnlichen Voraussetzungen der Biegungstheorie (Bd. 1, S. 792) die Differentialgleichung der elastischen Linie (Bd. 1, S. 793):
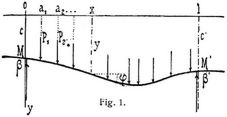
Bezeichnen für die Enden eines einfachen Balkens oder für die begrenzenden Stützen einer beliebigen Oeffnung eines durchlaufenden Balkens (Fig. 1) 0, l die Abszissen, c, c' die Ordinaten, β, β' die Tangenten der Neigungswinkel der elastischen Linie, M, M' die Biegungsmomente, und wird wie gewöhnlich das Produkt E J aus Elastizitätsmodul und Trägheitsmoment innerhalb der Oeffnung konstant angenommen (eventuell als Mittelwert), dann liefert 1. für beliebige Belastung die Tangente des Neigungswinkels der elastischen Linie bei x und die Gleichung der elastischen Linie [4], S. 6:
Hierin pflegt c bekannt zu sein, β an Einspannungsstellen ebenfalls (vgl. jedoch Einspannung), während allgemein ausgedrückt sind, [4], S. 7, 9:
Ueber die Ausdrücke von M, M' s. Balken, Bd. 1, S. 504, 505, 509; für den gewöhnlichen, beiderseits frei drehbaren Balken sind M = M' = 0. Die Summen Σ beziehen sich auf alle Lasten P zwischen den beigesetzten Grenzen; über ihre Werte für gleichmäßig verteilte und sonstige stetig verteilte Lasten s. Belastung der Träger.
In obigen Gleichungen ist der Einfluß der Vertikalkraft Vx vernachlässigt, wie dies meist geschieht, aber für die Berechnung der Formänderungen nicht allgemein zulässig ist (s. Biegungselastizität, Elastizitätsmodul, Einsenkung, vgl. Bd. 1, S. 520, 797). Soll derselbe berücksichtigt werden, so hat man beizufügen:
während 4. ungeändert bleibt. Für k, G gilt das in Bd. 1, S. 797, und Bd. 3 unter Elastizitätsmodul und Elastizitätsquotient Gesagte.
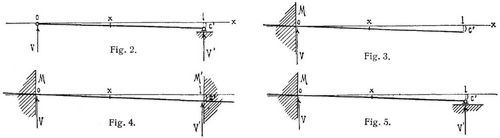
Wir erhalten hiernach mit Berücksichtigung des Einflusses von Vx beispielsweise für den gewöhnlichen, beiderseits frei drehbaren Balken (Fig. 2) wegen M = M' = 0 bei beliebiger Belastung:
mit
und speziell bei gleichmäßig verteilter Last von u pro Längeneinheit auf der ganzen Spannweite (vgl. Belastung):
worin bei gleichen Stützhöhen c' = 0. Für den einerseits festgespannten (unter einem Winkel φ,[377] für welchen β = tg φ), anderseits freischwebenden Balken (Fig. 3) gilt bei beliebiger Belastung der obenbestimmte allgemeine Ausdruck von y mit c = 0 und
bei gleichmäßig verteilter Last von u pro Längeneinheit auf der ganzen Spannweite:
Für andre Träger mit Stützenmomenten werden bei Berücksichtigung des Einflusses von Vx auf die Formänderungen auch die Stützenmomente selbst beeinflußt. Wird zur Abkürzung gesetzt
so erhält man für den beiderseits festgespannten Balken in dem gewöhnlich angenommenen Falle β = β' =c'/l (Fig. 4):
andernfalls sind beizufügen:
auf der rechten Seite von 13.
auf der rechten Seite von 14.
Bei zur Trägermitte μ symmetrischer Belastung jedoch werden aus 13., 14.:
so daß dann Vx keinen Einfluß auf die von der Belastung herrührenden M, M' ausübt. – Für den einerseits festgespannten, anderseits frei drehbaren Balken ist im Falle β = c'/l (Fig. 5):
während andernfalls rechts beizufügen wäre
Für durchlaufende Balken schließlich tritt an Stelle der in Bd. 1, S. 505, gegebenen Formeln bei gleich hohen oder in einer geneigten Geraden liegenden Stützpunkten:
wozu im Falle eingespannter Enden entsprechend den dort für diesen Fall gegebenen Gleichungen 20., 21. kommen:
Bei beliebigen Stützhöhen (beliebig innerhalb der zulässigen Grenzen, so daß tg φ gegen 1 zu vernachlässigen bleibt) wären beizufügen:
auf der rechten Seite von 17.
auf der rechten Seite von 18.
auf der rechten Seite von 19.
Mit s = 0 gehen die Formeln 13. bis 19. in die Bd. 1, S. 505, gegebenen über. Die jetzt bestimmten M, M' wären bei Berücksichtigung des Einflusses von Vx in der obengegebenen[378] Gleichung der elastischen Linie zu verwenden. Bezüglich der Summenausdrücke Σ bei stetig verteilter Last ist wieder auf den Art. Belastung zu verweisen.
Auf Grund vorstehender Gleichungen sind auch die in Bd. 1, S. 520, 521, angeführten Einsenkungen einfacher Balken berechnet. Ueber Balken mit sprungweise veränderlichem Querschnitt s. z.B. [4], S. 6, 22, über graphische Behandlung der elastischen Linie s. Biegungslinie und [2], [10], [11], [20], Auch andre Einflüsse als die obenerwähnten sind in der unten angeführten Literatur berücksichtigt. Die elastische Linie von Bogen (s.d.) pflegt, soweit nötig, durch Ermittlung der Aenderungen Δ x, Δ y, Δ φ der ursprünglichen x, y, φ bestimmt zu werden [15]. S.a. Einsenkung, Biegung, Gegenseitigkeit der Verrückungen, Betoneisenkonstruktionen und die an diesen stellen gegebene Literatur.
Literatur: [1] Winkler, Die Lehre von der Elastizität und Fettigkeit, Prag 1867, S. 79 u. f. – [2] Mohr, Beitrag zur Theorie der Holz- und Eisenkonstruktionen, Zeitschr. d. Arch.- u. Ingen.-Vereins zu Hannover 1868, S. 19. – [3] Ritter, Die elastische Linie und ihre Anwendung auf den kontinuierlichen Balken, Zürich 1871. – [4] Weyrauch, Allgemeine Theorie und Berechnung der kontinuierlichen und einfachen Träger, Leipzig 1873, S. 5, 22, 77, 80, 83, 89, 90. – [5] Ders., Die Gleichung der elastischen Linie beliebig belasteter gerader Stäbe, Zeitschr. f. Math. u. Physik 1873, S. 392. – [6] Ders., Die Gleichung der elastischen Linie beliebig belasteter gerader Stäbe bei gleichzeitiger Wirkung von Horizontal-(Axial-)Kräften, Zeitschr. f. Math. u. Physik 1874, S. 536. – [7] Ders., Temperatureinflüsse bei kontinuierlichen Trägern, Zeitschr. f. Baukunde 1879, S. 437. – [8] Castigliano, Théorie de l'équilibre des systèmes élastiques, Turin 1880, S. 203, 250 (deutsch von Hauff, Wien 1886, S. 199, 246). – [9] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 93, 132, 149, 150, 123, 270, 332. – [10] Winkler, Theorie der Brücken, Bd. 1, Aeußere Kräfte der Balkenträger, Wien 1886, S. 282, 313. – [11] Ritter, Anwendungen der graphischen Statik, Bd. 1, Zürich 1888, S. 161. – [12] Land, Einfluß der Schubkräfte auf die Biegung statisch bestimmter und die Berechnung statisch unbestimmter, gerader, vollwandiger Träger, Zeitschr. f. Bauwesen 1894, S. 611. – [13] Francke, Die elastische Linie des Balkens, Zeitschr. f. Bauwesen 1895, S. 439 (nachgebende Stützen berücksichtigt). – [14] Ders., Der steife Seilträger, Zeitschr. f. Bauwesen 1896, S. 567 (Mitwirkung von Horizontalkräften, vgl. [6]). – [15] Weyrauch, Die elastischen Bogenträger, ihre Theorie und Berechnung entsprechend den Bedürfnissen der Praxis, München 1897, S. 25, 190, 207, 223. – [16] Franke, Berechnung der Durchbiegung und der Nebenspannungen der Fachwerkträger, Zeitschr. f. Bauwesen 1898, S. 111. – [17] Handbuch der Ingenieurwissensch., Bd. 2, 2. Abt., Leipzig 1901, S. 251, 256. – [18] Schule, Die Biegungslehre gerader Stäbe mit veränderlichem Dehnungskoeffizienten (Elastizitätsmodul), Dinglers Polyt. Journal 1902, S. 149. – [19] Bach, Elastizität und Fettigkeit, Berlin 1902, S. 175, 249. – [20] Tetmajer, Die angewandte Elastizitäts- und Festigkeitslehre, Leipzig und Wien 1904, S. 31, 289, 357, 497, 504, 524, 528, 553.
Weyrauch.
http://www.zeno.org/Lueger-1904.