Ellipsenzirkel

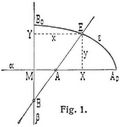
Ellipsenzirkel oder Ellipsograph ist ein Instrument, durch das Ellipsen mechanisch gezeichnet werden. Viele Ellipsenzirkel, die nur in ihrer praktischen Gestaltung verschieden sind, beruhen auf dem alten, schon von Proclus (410–485 u. Chr.) [1] mitgeteilten Bewegungsvorgang, daß ein Punkt E (Fig. 1) einer Geraden eine Ellipse s beschreibt, wenn zwei Punkte A, B dieser Geraden sich bezw. auf den senkrechten Geraden α, ß bewegen; s. Cardanische Kreise.

Es ist dann der Schnittpunkt M dieser beiden Geraden α, ß der Mittelpunkt der Ellipse ε, und es sind M A₀ = B E, M B₀ = A E die Halbachsen derselben. – Fällen wir von dem beschreibenden Punkt E auf die Geraden α, ß die Senkrechten E X = y, E Y = x und setzen die [437] Längen der Halbachsen B E = α, A E = b, so ist wegen der ähnlichen Dreiecke M A B ~ X A E ~ Y E B, MA/AB = x/a, MB/AB = y/b und folglich ergibt sich weil

ist, in rechtwinkligen Koordinaten x, y die Gleichung der von dem Punkte E betriebenen Ellipse: x²/a² + y²/b² = 1.

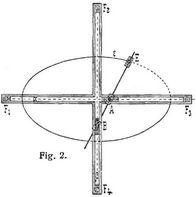
Bei der von B. Bramer [2] zuerst mitgeteilten und am meisten vorkommenden praktischen Ausführung in der schematischen Fig. 2 ist ein mit Schlitzen versehenes Kreuz, das auf vier an seinen Enden befindlichen Füßen F₁ F₂, F₃, F₄ über der Zeichnungsebene ruht, angewendet. In den Schlitzen bewegen sich Schlitten, die in den Punkten AB Achsen tragen. Auf diesen Achsen befinden sich unterhalb des Kreuzes drehbare Hülsen, durch die ein verschiebbarer prismatischer Stab geht und die vermittelst je einer Druckschraube auf diesem Stab festgestellt werden können. Dieser Stab trägt bei E eine in gleicher Weise feststellbare Hülfe mit einem Schreibstift und ist mit einer Millimeterteilung versehen, um den Ellipsenzirkel auf bestimmte Strecken, die den Ellipsenachsen entsprechen, einzuteilen. Der Schreibstift E an dem unterhalb des Kreuzes beweglichen Stabe beschreibt eine der Einstellung entsprechende vollständige Ellipse. Ellipsenzirkel dieser Art, die in vielen Einzelheiten vervollkommt sind, werden von C. Riefler in München-Nesselwang sorgfältig ausgeführt.

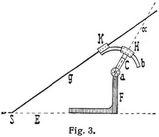
Auf dem Bewegungsvorgang, daß eine Gerade g (Fig. 3), die sich um eine feste Achse α dreht, eine Rotationskegelfläche und in einer Ebene E eine Ellipse, Hyperbel oder Parabel beschreibt, beruht ein von Barocius (1586) [3] zuerst ausgeführter Ellipsenzirkel. Derselbe ist nach der Ausführung von O. Günther in Braunschweig in Fig. 3 schematisch dargestellt. An dem auf der Zeichnungsebene E festgestellten Fuß F befindet sich ein Zylinder C, der um eine Achse a drehbar vermitteln einer Schraube bei a gegen den Fuß unter verschiedenen Winkeln festgeschraubt werden kann. Auf diesen Zylinder ist eine bogenförmige Hülfe H um die Zylinderachse α drehbar, und ein verschiebbarer Bogen b ist in dieser Hülfe vermitteln einer Schraube feststellbar. Der Bogen b ist mit einer Hülfe K versehen, in welcher der Stab g gleitet und dessen Schreibstift S bei entsprechender Einstellung eine Ellipse in der Zeichnungsebene E beschreibt.

Werden in einem Kreise die auf einem Durchmesser senkrechten Ordinaten in gleichem Verhältnis geteilt, so bilden die Teilpunkte eine Ellipse, deren große Achse dieser Durchmesser ist. Nach dieser geometrischen Beziehung hat W. Lehner einen im Prinzip neuen Ellipsenzirkel ausgeführt [4]. A. v. Braunmühl [5] hat in einer Abhandlung die ältesten Ellipsenzirkel mitgeteilt, und T. Rittershaus [6] hat in einer Abhandlung die mannigfaltigen Ausführungen der Ellipsenzirkel dargelegt.

Literatur: [1] Procli Diadochi in primum Euclidis elementarum librum Commentarii, Ed. Friedlein, Leipzig 1873, S. 106. – [2] Braunmühl, A. v., Zeitschr. f. Math. u. Physik, historisch-literärische Abteilung, 1890, Bd. 35, S. 161. – [3] Ebend. – [4] Katalog mathem. und mathem.-physikal. Modelle, Apparate und Instrumente, Nachtrag von W. Dyck, München 1893, S. 47. – [5] In diesem Katalog, München 1892, S. 54. – [6] Verhandlungen des Vereins zur Beförderung des Gewerbefleißes in Preußen, 1874, 53. Jahrg., S. 272.

Burmester.

Fig. 1.

Fig. 2.

Fig. 3.