Gegenseitigkeit der Verrückungen

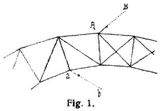
Gegenseitigkeit der Verrückungen. Begriff der Ingenieurmechanik und Elastizitätslehre. Im Jahre 1864 hat Maxwell [1] für die elastischen Formänderungen von Fachwerkträgern (s. Fachwerk) den Satz abgeleitet (Fig. 1): Durch eine an dem beliebigen Knotenpunkte A in beliebiger [344] Richtung A B wirkende Kraft 1 erleidet ein beliebiger Knotenpunkte in beliebiger Richtung a b die gleiche Verrückung, welche eine am Knotenpunkte a in der Richtung ab wirkende Kraft 1 für den Knotenpunkt A in der Richtung A B zur Folge hat.

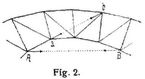
Dieser Satz von der Gegenseitigkeit der Verrückungen ergibt sich aus der Bd. 3, S. 554, erhaltenen Gleichung 9. unter der Voraussetzung a = 0 mit der zuvor gegebenen Gleichung 4., welche weiter liefern (Fig. 2): Durch zwei an den Knotenpunkten A, B in deren Verbindungsgeraden einander entgegenwirkende Kräfte 1 erleiden zwei Knotenpunkte a, b die gleiche Entfernungsänderung, welche zwei an den Knotenpunkten a, b in deren Verbindungsgeraden einander entgegenwirkende Kräfte 1 für die Entfernungsänderung der Knotenpunkte A, B zur Folge haben. Wie im letzteren Falle auf Grund jener Gleichung 4. die elastischen Formänderungen durch je zwei einander entgegengesetzte Kräfte in Beziehung zueinander gesetzt wurden, so lassen sich auf Grund der Bd. 3, S. 552, gegebenen allgemeinen Gleichung 3. Beziehungen für die elastischen Formänderungen durch andre Kräftegruppen ableiten [7], [10], [11], insbesondere auch die Gegenseitigkeit der Verdrehungen nachweisen. Die Sätze gelten unter den üblichen Voraussetzungen bezüglich reibungsloser Auflager, Knotengelenke u.s.w. nicht nur für die Knotenpunkte von Fachwerken, sondern auch für die Achspunkte gebogener stabförmiger Träger und selbst für die Punkte beliebiger isotroper fester Körper. Sie können gute Dienste bei Ermittlung der Formänderungen von Trägern und der Beanspruchung statisch unbestimmter Träger leisten, worüber die untenangeführte Literatur Aufschluß gibt. Beispielsweise ist die Einsenkung (s.d.) von A durch eine Last 1 in a ebenso groß wie die Einsenkung von a durch eine Last 1 in A und damit die elastische Linie (s.d.) durch eine Last 1 in A zugleich die Einflußlinie (s.d.) für die Einsenkung von A.

Literatur: [1] Maxwell, On the calculation of the equilibrium and stiffness of frames, Philosophical Magazine 1864, XXVII, S. 294. – [2] Mohr, Beitrag zur Theorie des Fachwerks, Zeitschr. des Arch.- und Ingen.-Ver. zu Hannover 1874, S. 509, und 1875, S. 17; Civilingen. 1885, S. 209. – [3] Castigliano, Intorno ad una proprietà dei sistemi elastici, Atti della R. Accademia delle science di Torino, 1882, XVII, S. 705. – [4] Swain, On the application of Virtual velocities to the determination of the deflection and stresses of frames, Journal of the Franklin Institute 1883, S. 101, 194, 250. – [5] Krohn, Der Satz von der Gegenseitigkeit der Verschiebungen und Anwendung desselben zur Berechnung statisch unbestimmter Fachwerkträger, Zeitschr. des Arch.- und Ingen.-Vereins zu Hannover 1884, S. 269. – [6] Forchheimer, Die Gegenseitigkeit der Verschiebungen, Zeitschr. des österr. Ingen.- und Arch.-Vereins 1886, S. 109. – [7] Land, Die Gegenseitigkeit elastischer Formänderungen als Grundlage einer allgemeinen Darstellung der Einflußlinien aller Trägerarten sowie einer allgemeinen Theorie der Träger überhaupt, Wochenblatt für Baukunde 1887, S. 14, 24, 33. – [8] de Fonviolant, Mémoire sur les déformations élastiques des pièces et des systemes des pièces à fibres moyennes planes ou gauches, Mémoires de la société des Ingenieurs civils 1888, II, S. 291. – [9] Steiner, Die Grundgesetze der Formänderung elastischer Körper, Wochenschr. des österr. Ingen.- und Arch.-Vereins 1889, S. 177. – [10] Müller-Breslau, Die graphische Statik der Baukonstruktionen, II, Leipzig 1903, S. 30, 46. – [11] Müller-Breslau, Die neueren Methoden der Festigkeitslehre, Leipzig 1904, S. 58, 181, 241. – [12] Ostenfeld, Technische Statik, Leipzig 1904, S. 256, 295.

Weyrauch.

Fig. 1.

Fig. 2.