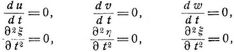- Elastizitäts- und Festigkeitslehre
Elastizitäts- und Festigkeitslehre, die Lehre von den angreifenden Kräften, widerstehenden Kräften und Formänderungen fetter Körper mit Rücksicht auf die Bedürfnisse der Technik. Es können also gegenüber der allgemeinen, Elastizitätslehre (s.d.) wesentliche Beschränkungen eintreten, während anderseits die behandelten Beziehungen bis zu praktischer Nutzbarkeit bei Beurteilung und Berechnung von Bauwerken und Maschinen durchgeführt werden sollen. Doch wird in der Elastizitäts- und Festigkeitslehre auf zusammengesetzte Konstruktionen entweder gar nicht oder nur so weit eingegangen, als sie nicht in besonderen Gebieten (Theorie der Ingenieurkonstruktionen, Maschinenbaukunde, graphische Statik u.s.w.) zweckmäßigere Erledigung finden.
Da auf Grund der allgemeinen Gleichungen für Spannungen und Verschiebungen (s. Elastizitätslehre, allgemeine) die Verhältnisse elastischer Bewegungen und anisotroper Körper trotz ihrer praktischen Wichtigkeit gegenwärtig nicht bis zu den obenerwähnten Zielen verfolgt werden können, so pflegt man jene Gleichungen, sofern sie überhaupt gegeben werden, auf das Gleichgewicht isotroper fester Körper zu beschränken, das heißt darin zu setzen:
sowie p nach der dortigen Gleichung 17), gewöhnlich mit τ = 0. Auch auf Grund der so vereinfachten Beziehungen konnten bisher nur für wenig Fälle praktisch brauchbare Resultate gewonnen werden, von welchen diejenigen von Hertz über die Beanspruchungen gegeneinander gedrückter Zylinder und Kugeln in dem Art. Auflager verwendet wurden, während die Saint-Venantsche Lösung des Torsionsproblems unter Torsionselastizität zu berücksichtigen sein wird.
In den meinen Fällen ist man genötigt, die Untersuchungen durch geeignete Annahmen zu erleichtern. Charakteristische Beispiele derselben wurden bei der Behandlung der Biegung, Bd. 1, S. 792, 793, besprochen. Dabei sind stets die Ergebnisse des Experiments und sonstiger Erfahrung, die mangelnde Isotropie des Materials und alle diejenigen Umstände im Auge zu behalten, welche auf die Zulässigkeit der fraglichen Annahmen Einfluß haben. Mitunter, wie bei der Betrachtung des durch eine gleichmäßig über seinen Querschnitt verteilte Kraft axial gezogenen Stabes, stehen die vereinfachten Ableitungen mit genaueren Lösungen im Einklang. In andern Fällen konnten sie durch genauere Lösungen von beschränkter Gültigkeit eine immerhin erwünschte Beleuchtung erfahren, wie die gewöhnliche Biegungstheorie durch Untersuchungen von Saint-Venant, Kirchhoff und Pochhammer (vgl. Bd. 1, S. 793; Bd. 2, S. 5). Eine wertvolle Bestätigung hat diese Biegungstheorie dadurch erhalten, daß sich volle Uebereinstimmung der durch Biegung und durch gewöhnlichen Zug experimentell bestimmten Werte des Elastizitätsmoduls ergab, nachdem man den Einfluß der Schubkräfte auf die Biegung rechnerisch zu berücksichtigen gelernt hatte (Bd. 1, S. 797; Bd. 3, S. 394).
In den letzten Jahrzehnten hat die Elastizitäts- und Festigkeitslehre durch die Mohrsche Verwendung des Prinzips der virtuellen Verrückungen in Verbindung mit dem Prinzip. der Koexistenz elastischer Verrückungen (s. Koexistenz) und durch die Berücksichtigung der Beziehungen für die Verschiebungsarbeit (s.d. und Clapeyrons Theorem, Fachwerke, statisch unbestimmte, kombinierte Träger, Gegenseitigkeit der Verrückungen) im Anschluß an Menabrea und Castigliano eine wesentliche Bereicherung ihrer Hilfsmittel erfahren, die sich besonders bei Abteilung statisch unbestimmter Stabkräfte und Stützenreaktionen sowie der Formänderungen von Ingenieurkonstruktionen geltend machte [12], [32].
Alle Ableitungen der Elastizitäts- und Festigkeitslehre müssen sich jedoch zunächst auf elastische Deformationen beschränken, eine theoretische Untersuchung der Verhältnisse bis zum Bruche ist gegenwärtig noch nicht möglich. Man sucht nun stets weit unter den Beanspruchungen zu bleiben, bei denen Trennungen oder schädliche Formänderungen zu befürchten wären (vgl. Fertigkeit, Elastizitätsgrenze, Dimensionenberechnung, zulässige Beanspruchung, Sicherheit, Festigkeitsbedingung); allein wie hierbei zuverlässig und doch wirtschaftlich zu verfahren ist, kann nur durch Zusammenwirken von Theorie und Erfahrung entschieden werden. Um die Mitte des vorigen Jahrhunderts mehrten sich die Versuche mit Konstruktionsmaterialien [2], [3], [4], [6] entsprechend der raschen Entwicklung der Eisenkonstruktionen und des Maschinenbaues. Nachdem die Theorien dieser Gebiete so weit gefördert waren, daß die wichtigsten Bedürfnisse klar erkannt werden konnten, mußte die nun auch durch staatliche Versuchsanstalten vermittelte genauere Kenntnis der Eigenschaften des Materials besonders befruchtend wirken. Es wurden[398] »Mitteilungen« der Münchner, Berliner, Züricher Versuchsanstalten begründet [9], [13], [14] und durch Bauschinger 1884 die »Konferenzen zur Vereinbarung einheitlicher Prüfungsmethoden für Bau- und Konstruktionsmaterialien« ins Leben gerufen [17], [18]. Man suchte die Ergebnisse der Versuche zusammenzufassen [6], [7], [15], [19] und im Gegensatze zum Vorgehen der vorausgegangenen Jahrzehnte schon bei der Darstellung und Weiterbildung der theoretischen Ableitungen zu verwerten [30], [31]. Auch die Beobachtungen an ausgeführten Konstruktionen, periodische Untersuchungen von Brücken und andern Bauwerken und Bruchproben zusammengesetzter Träger haben für die Entwicklung und Anwendung der Elastizitäts- und Festigkeitslehre eine immer wachsende Bedeutung erlangt. Insbesondere war aus den letzteren Verbuchen zu schließen, daß die gebräuchlichen Methoden der Berechnung von Trägern bei richtiger Anwendung und bei sorgfältiger Ausführung der Konstruktionen Resultate von befriedigender Zuverlässigkeit für die Praxis liefern (vgl. Fachwerke, Blechträger, Dimensionenberechnung, Nebenspannungen).
Bei der Ausdehnung des in Frage stehenden Gebietes müssen die einzelnen Begriffe desselben in zahlreichen besonderen Artikeln wie Zugelastizität, Zugfestigkeit, Zug, exzentrischer, Druckelastizität, Druckfestigkeit, Druck, exzentrischer, Knickfestigkeit, Biegungselastizität, Biegungsfestigkeit, Elastische Linie, Einsenkung, Elastizitätsmodul, Elastizitätsquotient und die bereits zitierten Stichworte behandelt werden, wobei auch die betreffende Spezialliteratur zu berücksichtigen sein wird.
Literatur: [1] Navier, Résumé des leçons donnés à l'école des ponts et chaussées sur l'application de la mécanique à l'établissement des constructions et des machines, I. De la résistance des corps solides, Paris 1826 (3. édition avec des notes et des appendices par Barré de Saint-Venant, Paris 1864). – [2] Morin, Résistance des matériaux, Paris 1853. – [3] Kirkaldy, Resultats of an experimental inquiry etc., London 1862. – [4] Winkler, Die Elastizitäts- und Festigkeitskoeffizienten, Civilingenieur 1863, S. 406. – [5] Winkler, Die Lehre von der Elastizität und Fertigkeit mit besonderer Rücksicht auf ihre Anwendung in der Technik, Prag 1867. – [6] v. Kaven, Kollektaneen über Schmiedeeisen, Stahl, Gußeisen, Zeitschr. d. Arch.- u. Ingenieur-Vereins zu Hannover 1868, S. 433. – [7] Styffe, Die Festigkeitseigenschaften von Eisen und Stahl, Weimar 1876. – [8] Winkler, Abriß der Geschichte der Elastizitätslehre, Technische Blätter 1871, S. 22, 232. – [9] Mitteilungen aus dem mechanisch-technischen Laboratorium der Technischen Hochschule München, 1. Heft 1873, 29. Heft 1904. – [10] Müller-Breslau, Elementares Handbuch der Festigkeitslehre, Berlin 1875. – [11] Grashof, Theorie der Elastizität und Festigkeit mit Bezug auf ihre Anwendungen in der Technik, Berlin 1878 (1. Aufl. 1866). – [12] Castigliano, Théorie de l'équilibre des systèmes élastiques et ses applications, Turin 1880 (deutsch von Hauff, Wien 1886). – [13] Mitteilungen aus den technischen Versuchsanstalten zu Berlin, 1. Jahrg. 1883, 23. Jahrg. 1905. – [14] Mitteilungen der Anstalt zur Prüfung von Baumaterialien am Polytechnikum in Zürich, 1. Heft 1884, 9. Heft 1900. – [15] Confidère, Mémoire sur l'emploi du fer et de l'acier dans les constructions, Paris 1885 (deutsch von Hauff, Wien 1888). – [16] Vigreux, Traité théorique et pratique de la résistance des matériaux, Paris 1885. – [17] Verhandlungen der Kongresse zur Vereinbarung einheitlicher Prüfungsmethoden, Münchener Mitteilungen, 14. Heft 1886 (Konferenz zu München 1884); 22. Heft 1894 (Konferenzen zu Dresden 1886 und Berlin 1890); 23. Heft 1895 (Konferenz zu Wien 1893). – [18] Beschlüsse der Konferenzen zu München und Dresden über einheitliche Untersuchungsmethoden, München 1887. – [19] Weyrauch, Die Festigkeitseigenschaften und Methoden der Dimensionenberechnung von Eisen- und Stahlkonstruktionen, Leipzig 1889. (1. Aufl. 1876). – [20] Mitteilungen des Technologischen Gewerbemuseums in Wien, Neue Folge, 1. Jahrg. 1891, 15. Jahrg. 1905. – [21] Keck, Vorlesungen über Elastizitätslehre als Grundlage für die Festigkeitsberechnung der Bauwerke, Hannover 1893. – [22] Commission des méthodes d'essai des matériaux de construction, Paris 1894. – [23] Rudeloff, Untersuchungen über den Einfluß der Kälte auf die Festigkeitseigenschaften von Eisen und Stahl, Mitteil. aus d. techn. Versuchsanstalten zu Berlin, 1895, S. 197. – [24] Ledebur, Der Einfluß der Temperatur auf die Festigkeitseigenschaften der Metalle, insbesondere des Eisens, Zeitschr. d. Ver. deutsch. Ingenieure 1896, S. 565, 596, 635. – [25] Kirsch, Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre, Zeitschr. d. Ver. deutsch. Ingenieure 1898, S. 797. – [26] Martens, Handbuch der Materialienkunde für Maschinenbau, I, Berlin 1898. – [27] Résal, Résistance des matériaux, Paris 1898. – [28] Foeppl, Vorlesungen über technische Mechanik, III. Festigkeitslehre, Leipzig 1900. – [29] Handbuch der Ingenieurwissenschaften, Bd. 2, 2. Abteilung, Leipzig 1901, S. 66 (Der Baustoff und seine Widerstände). – [30] Tetmajer, Die angewandte Elastizitäts- und Festigkeitslehre, auf Grund der Erfahrung, Leipzig und Wien 1904 (1. Aufl. 1889). – [31] Müller-Breslau, Die neueren Methoden der Festigkeitslehre und der Statik der Baukonstruktionen, Leipzig 1904 (1. Aufl. 1886). – [32] Handbuch der Architektur, Bd. 1, 1. Heft: Die Technik der wichtigsten Baustoffe, Stuttgart 1905. – [33] Brauer, Die Festigkeitslehre, Leipzig 1905. – [34] Bach, Elastizität und Fertigkeit, die für die Technik wichtigsten Sätze und deren erfahrungsmäßige Grundlage, Stuttgart 1905 (1. Aufl. 1889/90).
Weyrauch.
http://www.zeno.org/Lueger-1904.