- Geschwindigkeitskomponenten
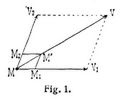
Geschwindigkeitskomponenten. Ein bewegter Punkt befinde sich zur Zeit t in M (Fig. 1), zur Zeit t + dt in M', er hat in dem Zeitelement dt die Verschiebung MM' erfahren und seine Geschwindigkeit ist die gerichtete (geometrische) Größe, die aus der Verschiebung MM' durch Division mit dt hervorgeht. Die Verschiebung MM' kann man sich in Teilverschiebungen (Komponenten) MM1 und M1M' (oder auch MM2 und M2M', wo MM2 = M1M' und MM1 = M2M' ist) zerlegt denken, deren geometrische Summe die ursprüngliche Verschiebung ist. Werden diese Teilverschiebungen durch das Zeitelement dt dividiert, so entstehen neue gerichtete Größen: die Komponenten der Geschwindigkeit.
Trägt man von M aus die Geschwindigkeit und ihre Komponenten als gerichtete Größen auf, so entsteht eine Figur MV1VV2, die der unendlich kleinen Figur MM1M' M2 ähnlich ist und das Parallelogramm der Geschwindigkeiten heißt. Nach derselben ist die Geschwindigkeit gleich der Diagonale des Parallelogramms, dessen Seiten die Geschwindigkeitskomponenten sind. Wird die ursprüngliche Verschiebung in mehr als zwei Teilverschiebungen zerlegt, so entstehen bei Division derselben ebenso viele Geschwindigkeitskomponenten, aus denen sich die Geschwindigkeit als geometrische Summe mittels des Polygons der Geschwindigkeiten zusammensetzt. Die Zerlegung einer Geschwindigkeit in zwei Komponenten mit vorgegebener Richtung ist möglich und bestimmt, wenn die gegebenen Richtungen mit jener der Geschwindigkeit in einer Ebene liegen. Eine Zerlegung nach drei vorgegebenen Richtungen ist immer möglich und bestimmt, wenn die Richtungen nicht in einer Ebene liegen. Der rein formalen Zerlegung der Geschwindigkeit in zwei Komponenten kann man einen realen Sinn unterlegen, wenn man sich vorstellt, daß sich der Punkt relativ zu einem Koordinatensystem mit der einen Komponente als Geschwindigkeit bewegt, während das Koordinatensystem eine Translation mit der Geschwindigkeit der andern Komponente erfährt (s. Bewegung, relative).
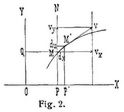
Die Zerlegung der Geschwindigkeit erfolgt meistens in Richtung der Koordinatenlinien, wie aus folgenden Beispielen ersichtlich ist: Spezielle Fälle: 1. Ein Punkt beschreibe eine ebene Kurve und es werde dieselbe auf ein rechtwinkliges Koordinatensystem der x, y bezogen (Fig. 2). Man hat vx = dx/dt, vy = dy/dt, v2 = vx2 + vy2. Zugleich sind vx, vy die Geschwindigkeiten der Bewegung der Projektionspunkte P, Q von M auf die Koordinatenachsen und es stellt vy : vx die [433] Tangente der Neigung von v gegen die x-Achse dar. Sind die Koordinaten x, y als Funktionen der Zeit t gegeben, so erhält man durch deren Differentation die Komponenten der Geschwindigkeit. – Aehnlich erhält man für dreiachsige Koordinatensysteme: vx = dx/dt, vy = dy/dt, vz = dz/dt; v2 = vx2 + vy2 + vz2; cosα/vx = cosβ/vy = cosγ/vz = 1/v, wenn α, β, γ die Richtungswinkel der Geschwindigkeit oder Bahntangente sind.
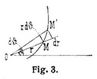
2. In einem ebenen Polarkoordinatensystem der rϑ (Fig. 3) sind dr und rdϑ die Bogenelemente der Koordinatenlinien und daher die Komponenten der Geschwindigkeit
Es ist ferner:
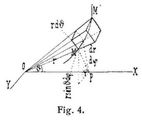
3. Für das räumliche Polarkoordinatensystem der r, ϑ, φ (Fig. 4), nämlich des Radiusvektors QM = r, des Winkels ϑ, den dieser mit der Polarachse OX, und des Winkels φ, den die Ebene des Winkels ϑ mit der Fundamentalebene XOY bildet, sind die Bogenelemente der Koordinatenlinien dr, rdφ, r sinϑdφ und die drei entsprechenden Komponenten der Geschwindigkeit
Sie sind alle drei zueinander senkrecht und es liefern vϑ und vφ die Geschwindigkeit der sphärischen Bewegung, deren Quadrat
mit vr2 zusammen
das Quadrat der Geschwindigkeit der räumlichen Bewegung ausmacht.
Literatur: Schell, Theorie der Bewegungen und der Kräfte, Leipzig 1879, Bd. 1, S. 199 bis 204.
Finsterwalder.
http://www.zeno.org/Lueger-1904.