Guldinsche Regeln

Guldinsche Regeln. Diesen Namen führen zwei Sätze über den Schwerpunkt homogener ebener Linien und Flächenräume, die sich bereits bei dem griechischen Mathematiker Pappus (Collectiones mathematicae, lib. VII) finden, aber von Guldin (geb. 1577, gest. 1663) in seinen Werken »De centro gravitatis«, 1635 und »Centrobaryca« 1643 reproduziert wurden.

1. Der Inhalt einer von einem ebenen Kurvenbogen erzeugten Rotationsfläche ist gleich dem Produkt aus der Länge des rotierenden Bogens und des Weges, den sein Schwerpunkt bei der Erzeugung der Fläche beschreibt.

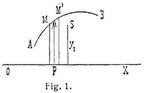
Es sei MM' (Fig. 1) eine Seite eines ebenen Polygons A M B; μ ihre Mitte und μp ihr Abstand von einer Achse O X in der Ebene der Fig. 1, sowie y₁ der Abstand des Schwerpunkts S der gebrochenen Linie A M B von dieser Achse, dann ist das Moment von S gleich der Summe der Momente der einzelnen Polygonseiten, nämlich y₁ ∙ Σ(MM') = Σ (MM' ∙ μp). Läßt man nun das Polygon um die Achse rotieren, so erzeugt die Seite M M' die Oberfläche 2π ∙ MM' ∙ μp eines Kegelstumpfes, das Polygon selbst also die Oberfläche Ω = 2 πΣ (MM' ∙ μp) = 2 πy₁ ∙ Σ (MM'). Es ist aber 2 πy₁ der bei der Rotation vom Schwerpunkt S beschriebene Kreisumfang. Geht das Polygon in eine Kurve von der Länge s über, so wird die Oberfläche der Kegelstumpfsumme zu der von der Kurve erzeugten Rotationsfläche, und man erhält den Satz: Ω = 2 πy1s. Rotiert der Bogen nicht um 2π, sondern nur um ϑ, so gilt der Satz gleichfalls, denn ist Ω' die Oberfläche, die der Teilrotation entspricht, so ist Ω' : Ω = ϑ : 2π, also Ω' = ϑ (Ω : 2π) = ϑy₁s, wo ϑy₁ den von S bei der Teilrotation beschriebenen Weg darstellt. Die Lage von s gegen die Achse S übt keinen Einfluß auf den Inhalt der Oberfläche aus, solange der Abstand y₁ derselbe bleibt und s die Achse nicht schneidet.

2. Das Volumen eines Rotationskörpers ist das Produkt aus dem Inhalt des rotierenden ebenen Flächenraumes und des Weges, den sein Schwerpunkt bei der Rotation beschreibt.

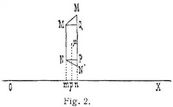
Es werde der homogene Flächenraum einer ebenen Kurve als die Grenze einer Summe von ihr eingetriebener Rechtecke M N P Q (Fig. 2) senkrecht zu einer Achse O X in der Ebene der Kurve angesehen; dann ist das Moment einer solchen in bezug auf diese Achse M N N P μ p, wenn up der Abstand seines Schwerpunktes von der Achse ist. Ist m die lotrechte Projektion von M auf die Achse, so wird MN = Mm – Nm und, μ p = ¹/₂(Mm + Nm), also das Moment i (Mm² – Nm²) N P. Ist also y₁ der Abstand des Schwerpunktes der Summe der Rechtecke von der Achse, so sind y₁ + Σ ∙ (MNPQ) = ¹/₂ (Mm² – Nm²) N P. Rotiert nun die Figur um die Achse O X, so erzeugt jedes Rechteck ein Volumen gleich der Differenz zweier Zylinder, π(Mm² – Nm²) N P und wird mithin das erzeugte Gesamtvolumen V = π Σ (Mm² – Nm²) N P und daher V = 2 π y₁ Σ (M N P Q). Geht nun die Summe der Rechtecke in die Fläche F der Kurve über, so wird V das Volumen des von ihr erzeugten Rotationskörpers darstellen und es drückt die Relation V = 2 π y₁ ∙ F den erwähnten Satz aus. Auch dieser Satz gilt für Teilrotationen, wie leicht zu sehen. Schneidet die Achse O X die rotierende Fläche, so liefert der Satz unmittelbar angewendet die Differenz der Volumina der Rotationskörper, die von den zu beiden Seiten der Drehachse gelegenen Flächenstücken beschrieben werden. Beide Guldinsche Regeln sind übrigens leicht zu übersehender Ausdehnungen fähig auf Gebilde, die entstehen, wenn die Achse während ihrer Erzeugung kontinuierlich wechselt.

(Schell) Finsterwalder.

Fig. 1.

Fig. 2.