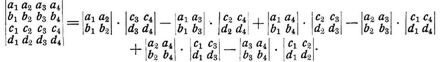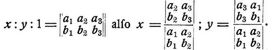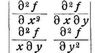- Determinanten
Determinanten sind symbolische Ausdrücke für häufig vorkommende Eliminationsresultate, um die an sich schwerfälligen Ausdrücke in einfacher, übersichtlicher und für die Rechnung brauchbarer Gestalt schreiben zu können.
Diese spielen in neuerer Zeit fast in allen Teilen der Mathematik eine bedeutende Rolle, am meisten in der Invariantentheorie und analytischen Geometrie.
1. Zweireihige Determinante. Das Eliminationsresultat von x (x-Eliminat) aus den Gleichungen
ist a1b1 – a2b2 = 0 und wird als Determinante
geschrieben; a1 a2, b1, b2 heißen Elemente, a1b2 und a2b1 Glieder der Determinante. Die Reihen a1a2 und b1b2 sind Horizontalreihen (Zeilen), die Reihen a1b1 und a2b2 Vertikalreihen (Kolonnen). Ebenso bei mehrreihigen Determinanten.
2. Dreireihige Determinante.
Das xy-Eliminat aus den Gleichungen:
lautet in Determinantenform
in gewöhnlicher Form: a1b2c3 – a1b3c2 + a2b3c1 – a2b1c3 + a3b1c2 – a3b2c1 = 0.
3. Wertermittlung der Determinante. Man erhält sämtliche Glieder aus dem Diagonalglied (im Beispiel 2: a1b2c3), indem man alle Permutationen der Indices bildet; ein solches Glied hat {positives/negatives} Vorzeichen, je nachdem die betreffende Permutation eine {gerade/ungerade} Anzahl von Inversionen besitzt (z.B. hat a2b1c3 eine, a2b3c1 zwei Inversionen). Bequemer zur Wertermittlung ist im allgemeinen die Entwicklung nach den Elementen einer Zeile oder Kolonne. Obige dreireihige Determinante kann nämlich auch geschrieben werden:
Hier sind die Elemente der ersten Zeile multipliziert mit ihren Unterdeterminanten (Minoren), die aus der Determinante dadurch entstehen, daß je die Zeile und die Kolonne, die das betreffende Element enthalten, weggelassen werden. Ebenso könnte man die Determinante nach den Elementen einer beliebigen Zeile oder Kolonne entwickeln. Das Element, dessen Unterdeterminante gesucht wird, hat man sich durch cyklische Vertauschung an die erste Stelle gebracht zu denken; z.B. aus
ergibt sich
als Unterdeterminante von b2. Doch muß dieses Verfahren der Wertermittlung bei Determinanten von gerader Reihenzahl insofern modifiziert werden, als die abwechselnden Unterdeterminanten abwechselnde Vorzeichen erhalten, es ist z.B.:
4. Hauptsätze der Determinantenlehre.
α. Eine Determinante bleibt ungeändert, wenn man ihre Zeilen zu Kolonnen macht und umgekehrt:
ß. Bei Vertauschung zweier parallelen Reihen wechselt die Determinante ihr Zeichen:
[723] γ. Eine Determinante mit zwei gleichen Parallelreihen verschwindet identisch:
δ. Eine Determinante wird mit einem Faktor multipliziert, indem man jedes Element einer
Reihe mit dem Faktor multipliziert:
ε. Bestehen die Elemente einer Reihe aus Summen, so ist die Determinante selbst in eine Summe von Determinanten zerlegbar:
ζ. Eine Determinante bleibt ungeändert, wenn man zu den Elementen einer Reihe die gleichvielfachen Elemente einer Parallelreihe addiert:
5. Laplacescher Determinantensatz. Die unter 3. erwähnten Unterdeterminanten können wieder nach Elementen einer Reihe entwickelt werden. Die hierbei auftretenden Unterdeterminanten heißen Unterdeterminanten 2. Ordnung u.s.w. – Der Laplacesche Determinantensatz lautet diesbezüglich: Jede n reihige Determinante kann als Summe von Produkten von Unterdeterminanten p. Ordnung mit solchen (n – p). Ordnung dargestellt werden, z.B.:
6. Multiplikation der Determinanten. Zwei n-reihige Determinanten werden multipliziert, indem man die einzelnen Elemente einer Reihe mit den entsprechenden einer andern multipliziert, addiert und aus den für alle Reihenkombinationen gebildeten Summen eine neue Determinante bildet:
7. Matricen. Matrix heißt eine Determinante mit weniger Zeilen als Kolonnen, z.B.:
Die Determinanten, die man durch Weglassen von Kolonnen aus ihr bildet, in unserm Beispiel:
heißen die Determinanten der Matrix. Als Quadrat obiger Matrix wird die Größe
bezeichnet.
Als Summe dreier Quadrate verschwindet das Matrixquadrat nur dann, wenn alle drei Determinanten der Matrix Null sind. Der Ausdruck
bedeutet, daß sich x : y : z wie die Determinanten obiger Matrix verhalten.
8. Anwendungen der Determinanten.
α. Auflösung eines Systems linearer Gleichungen, z.B.:
Es ist
ß. Elimination von x aus
γ. Differenzenproduktsdeterminante. Dieselbe ist:
Dieselbe spielt bei den symmetrischen Funktionen (s. Symmetrisch) eine Rolle.
δ. Resultante zweier Gleichungen von höherem Grad, s. Resultante.
ε. Funktionaldeterminante, s.d.
ζ. Hessesche Determinante heißt die Determinante der zweiten Differentialquotienten einer homogenen Funktion (Form). Bei zwei homogenen Veränderlichen x und y ist dieselbe, wenn f (x, y) die gegebene Form ist:
eine in der Invariantentheorie sehr wichtige Bildung. Die Hessesche Determinante für drei homogene Veränderliche s. Hessesche Kurve.
[724] ŋ. Beispiel einer Anwendung auf analytische Geometrie. Sind in der Ebene drei Punkte in rechtwinkligen Koordinaten x1y1, x2y2, x3y3 gegeben, so ist der Flächeninhalt des von ihnen gebildeten Dreiecks:
Die Determinante gleich Null gesetzt ist die Bedingung, daß die drei Punkte auf einer Geraden liegen; daher ist
die Gleichung der Verbindungslinie der zwei Punkte (x1y1) und (x2y2).
ϑ. Beispiel einer Anwendung auf Goniometrie:
Literatur: Unter den nachstehend aufgeführten Werken ist [1] das reichhaltigste, aber etwas abstrakt; [4], [5] und [6] dienen zur ersten Einführung; [5] und [6] enthalten viele Uebungsbeispiele. [1] Baltzer, R., Theorie und Anwendung der Determinanten, 5. Aufl., Leipzig 1881. – [2] Salmon, G., Vorlesungen über die Algebra der linearen Transformationen, deutsch von W. Fiedler, 2. Aufl., Leipzig 1877. – [3] Gordan, P., Vorlesungen über Invariantentheorie, herausgegeben von Kerschensteiner, Bd. 1, Leipzig 1885. – [4] Diekmann, J, Anwendung der Determinanten und Elemente der neueren Algebra, Leipzig 1889. – [5] Mansion, P., Elemente der Theorie der Determinanten, 3. Aufl., Leipzig 1902. – [6] Dölp, H., Die Determinanten, 6. Aufl., Darmstadt 1903. – [7] Kronecker, L., Vorlesungen über die Theorie der Determinanten, I, Leipzig 1903. – [8] Pascal, E., Die Determinanten, deutsch von Leitemann, Leipzig 1900.
Wölffing.
http://www.zeno.org/Lueger-1904.