- Involution
Involution ist allgemein die Anordnung der Punkte einer Punktreihe (der Strahlen, Ebenen, Kurven u.s.w. eines Büschels) in Systeme von je n Punkten derart, daß jeder Punkt nur zu einem System gehört. Die Punktinvolutionen werden auf Geraden durch Kurven- oder Flächenbüschel ausgeschnitten. Sie heißen höhere Involutionen, wenn n > 2 ist.
Wölffing.
Werden zwei projektive Punktreihen so aufeinander gelegt, daß die nicht entsprechenden Endpunkte entsprechend gleicher Strecken, z.B.
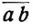 und
und 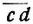 (Fig. 1), zur Deckung gelangen, so entsteht hierdurch auf der Geraden ein Punktsystem: eine Involution von Punkten, eine involutorische Punktreihe oder ein involutorisches gerades Gebilde genannt.
(Fig. 1), zur Deckung gelangen, so entsteht hierdurch auf der Geraden ein Punktsystem: eine Involution von Punkten, eine involutorische Punktreihe oder ein involutorisches gerades Gebilde genannt.Dem unendlich fernen Punkte des Trägers der Involution entspricht ein bestimmter Punkt, der Mittelpunkt der Involution. Die entsprechenden Endpunkte entsprechend gleicher Strecken bilden je ein zusammengehöriges oder konjugiertes Punktpaar der Involution. Man bezeichnet zusammengehörige Punkte zweckmäßig mit den gleichen Buchstaben und versteht den einen Buchstaben mit einem Index, z.B. a a1, b b1 u.s.w. (Fig. 2). Durch zwei konjugierte Punktpaare ist die Involution vollständig bestimmt. Es gibt eine ungleichlaufende oder hyperbolische und eine gleichlaufende oder elliptische Involution; im ersten Falle ist die durch ein konjugiertes Punktpaar gebildete Strecke durch die übrigen Punktpaare nicht getrennt, im letzteren Falle findet eine solche Trennung statt; eine hyperbolische Involution besitzt stets zwei Doppelpunkte, bei einer elliptischen Involution sind Doppelpunkte nicht vorhanden.
Für eine Involution von Punkten gilt für jedes konjugierte Punktpaar a a1, b b1 u.s.w., wenn m den Mittelpunkt der Involution bezeichnet, die Beziehung:
Für den Fall des Vorhandenseins von Doppelpunkten g und h erhält man
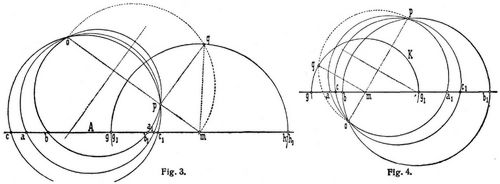
woraus folgt, daß die Doppelpunkte mit jedem konjugierten Punktpaar der Involution je vier harmonische Punkte bilden. Es unterliegt keiner Schwierigkeit, beliebig viele Punktpaare einer Involution zu konstruieren, sobald zwei Punktpaare derselben gegeben sind. Legt man nämlich durch die Punkte a a1 bezw. b b1 (Fig. 3) zwei Kreise, die sich in den Punkten o und p schneiden, so liefert jeder weitere durch o und p gehende Kreis auf dem Träger der Involution ein konjugiertes Punktpaar derselben, denn es findet ja die Beziehung statt:
[210] Liegen die Punkte o und p auf derselben Seite von A, so liegt der Punkt m auf der Verlängerung von o p und unter den Kreisen von o p sind zwei Kreise vorhanden, welche A in den Punkten g und h, den Doppelpunkten der Involution, berühren. Ihr Abstand von m ist gleich der Strecke
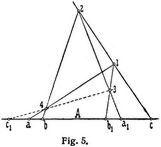
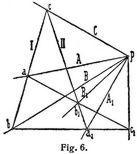
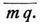 Liegen aber die Punkte o und p auf verschiedenen Seiten von A, so sind keine den Träger berührenden Kreise durch o und p und demnach auch keine Doppelpunkte der Involution möglich; dagegen gibt es ein konjugiertes Punktpaar g g1 das symmetrisch zum Mittelpunkt m liegt und von dem Kreise K (Fig. 4) auf dem Träger der Involution ausgeschnitten wird. – Verbindet man die Punkte einer Involution mit einem beliebigen außerhalb des Trägers der Involution, gewählten Punkte, so entsteht eine Involution von Strahlen oder eine Strahleninvolution, die je nach der zugrunde gelegten Punktinvolution zwei Doppelstrahlen besitzen oder ohne solche Doppelstrahlen sein kann; im ersten Falle heißt sie eine hyperbolische, im zweiten Falle eine elliptische Strahleninvolution. Der genannte Punkt außerhalb des Trägers kann so gewählt werden, daß a) im Falle der elliptischen Involution die konjugierten Strahlen aufeinander senkrecht stehen; b) im Fall der hyperbolischen Involution die Doppelstrahlen aufeinander senkrecht stehen und den Winkel bezw. Außenwinkel je zweier konjugierten halbieren. Sowohl für eine Punkt- wie für eine Strahleninvolution läßt sich in einfacher Weise linear zu einem gegebenen Punkte bezw. Strahle der konjugierte Punkt bezw. Strahl konstruieren, wenn die Involution durch zwei konjugierte Elementenpaare gegeben ist. Bei der Punktinvolution beruht die Konstruktion auf dem Satze, daß die drei Paar Gegenseiten eines vollständigen Viereckes von irgend einer Geraden nach Punktpaaren einer Involution getroffen werden; bei der Strahleninvolution liegt der Satz zugrunde, daß die Verbindungslinien eines beliebigen Punktes mit den Gegenecken eines vollständigen Vierseits drei Strahlenpaare einer Involution liefern. Es ergeben sich folgende lineare Konstruktionen: Ist c (Fig. 5) ein Punkt einer Punktinvolution a a1, b b1, so zieht man durch c eine willkürliche Gerade, wählt auf ihr die Punkte 1 und 2 beliebig und verbindet diese mit den gegebenen Punktpaaren a a1 und b b1. Die Verbindungslinie 1b1 und 2a1 ebenso 1a und 2b liefern die Punkte 3 und 4 so, daß die Linie 3 4 den dem Punkte c konjugierten Punkt c1 auf A ausschneidet. Ist entsprechend C (Fig. 6) ein Strahl der Strahleninvolution A A1 B B1, so wählt man auf C einen beliebigen Punkt c und zieht durch ihn die Strahlen I und II, welche die Strahlenpaare A A1 und B B1 in den Punkten a1 und b b1 so treffen, daß die Verbindungslinien a b1 und a1 b sich in einem Punkte c1 schneiden, durch welchen der dem Strahle C konjugierte Strahl C1 der Involution hindurchgeht. Jeder Kegelschnittbüschel, ebenso jeder Flächenbüschel II. Ordnung erzeugt auf jeder Geraden eine Involution.
Liegen aber die Punkte o und p auf verschiedenen Seiten von A, so sind keine den Träger berührenden Kreise durch o und p und demnach auch keine Doppelpunkte der Involution möglich; dagegen gibt es ein konjugiertes Punktpaar g g1 das symmetrisch zum Mittelpunkt m liegt und von dem Kreise K (Fig. 4) auf dem Träger der Involution ausgeschnitten wird. – Verbindet man die Punkte einer Involution mit einem beliebigen außerhalb des Trägers der Involution, gewählten Punkte, so entsteht eine Involution von Strahlen oder eine Strahleninvolution, die je nach der zugrunde gelegten Punktinvolution zwei Doppelstrahlen besitzen oder ohne solche Doppelstrahlen sein kann; im ersten Falle heißt sie eine hyperbolische, im zweiten Falle eine elliptische Strahleninvolution. Der genannte Punkt außerhalb des Trägers kann so gewählt werden, daß a) im Falle der elliptischen Involution die konjugierten Strahlen aufeinander senkrecht stehen; b) im Fall der hyperbolischen Involution die Doppelstrahlen aufeinander senkrecht stehen und den Winkel bezw. Außenwinkel je zweier konjugierten halbieren. Sowohl für eine Punkt- wie für eine Strahleninvolution läßt sich in einfacher Weise linear zu einem gegebenen Punkte bezw. Strahle der konjugierte Punkt bezw. Strahl konstruieren, wenn die Involution durch zwei konjugierte Elementenpaare gegeben ist. Bei der Punktinvolution beruht die Konstruktion auf dem Satze, daß die drei Paar Gegenseiten eines vollständigen Viereckes von irgend einer Geraden nach Punktpaaren einer Involution getroffen werden; bei der Strahleninvolution liegt der Satz zugrunde, daß die Verbindungslinien eines beliebigen Punktes mit den Gegenecken eines vollständigen Vierseits drei Strahlenpaare einer Involution liefern. Es ergeben sich folgende lineare Konstruktionen: Ist c (Fig. 5) ein Punkt einer Punktinvolution a a1, b b1, so zieht man durch c eine willkürliche Gerade, wählt auf ihr die Punkte 1 und 2 beliebig und verbindet diese mit den gegebenen Punktpaaren a a1 und b b1. Die Verbindungslinie 1b1 und 2a1 ebenso 1a und 2b liefern die Punkte 3 und 4 so, daß die Linie 3 4 den dem Punkte c konjugierten Punkt c1 auf A ausschneidet. Ist entsprechend C (Fig. 6) ein Strahl der Strahleninvolution A A1 B B1, so wählt man auf C einen beliebigen Punkt c und zieht durch ihn die Strahlen I und II, welche die Strahlenpaare A A1 und B B1 in den Punkten a1 und b b1 so treffen, daß die Verbindungslinien a b1 und a1 b sich in einem Punkte c1 schneiden, durch welchen der dem Strahle C konjugierte Strahl C1 der Involution hindurchgeht. Jeder Kegelschnittbüschel, ebenso jeder Flächenbüschel II. Ordnung erzeugt auf jeder Geraden eine Involution.Vonderlinn.
http://www.zeno.org/Lueger-1904.