Körper von gleichem Widerstande

Körper von gleichem Widerstande heißen in der Elastizitäts- und Festigkeitslehre stabförmige Körper, für welche die bei der Dimensionierung maßgebenden Beanspruchungen in allen Querschnitten gleich groß sind.

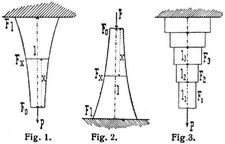
Ein gerader Stab mit vertikaler Achse sei durch eine auf den Endquerschnitt F₀ gleichmäßig verteilte Last P und sein eignes Gewicht von γ pro Volumeneinheit belastet (Fig. 1 und 2). Die Beanspruchung pro Flächeneinheit soll in allen Querschnitten σ betragen. Biegungen sind ausgeschlossen. Dann erhält man den nötigen Querschnitt F_x in Entfernung x von F₀ und das Stabgewicht G_x von F₀ bis F_x (V_x entsprechendes Volumen):

Soll der wie oben belastete Stab aus einzelnen Teilen der Längen l₁, l₂, ... und konstanter Querschnitte so hergestellt werden (Fig. 3), daß die größten Beanspruchungen aller dieser Teile von gleichem Werte σ und, dann folgen die Querschnitte:

wonach der Querschnitt des m ten Stabes von P aus allgemein und speziell begleichen Längen l:

S. a. Zugelastizität.

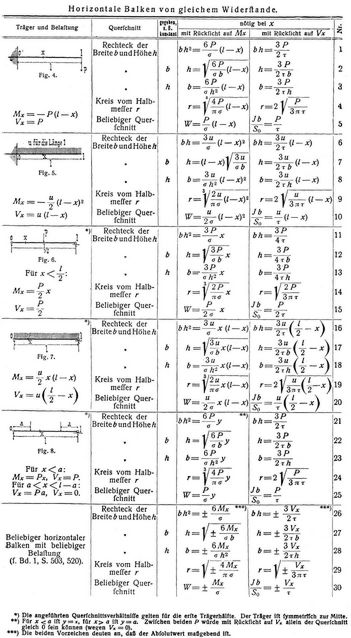
Bei gebogenen Stäben, Balken und Bogen (s.d.) pflegt bekanntlich die Dimensionierung auf Grund der größten Normalspannungen in den einzelnen Querschnitten zu erfolgen, was bei Berücksichtigung entsprechender Versuche über die Biegungsfestigkeit (s.d.) dann berechtigt ist, wenn sich übersehen läßt, daß zugleich genügende Sicherheit gegen die auftretenden Schubspannungen erreicht wird. Dies trifft indessen für horizontale Balken als Körper von gleichem Widerstande gewöhnlich nicht zu. Bezeichnen für einen solchen σ, τ die größten zulässigen Normalspannungen und Schubspannungen in den Querschnittselementen, M_x, V_x das Biegungsmoment und die Vertikalkraft in einem beliebigen Querschnitte, x J, W das Trägheitsmoment und Widerstandsmoment desselben, b die Breite der Achsschicht und S₀ das statische Moment des Querschnittsteils auf einer Seite der Achsschicht in Hinsicht der letzteren, dann ist gegenüber den durch M_x erzeugten Normalspannungen nötig:

W = ± M_x/σ,

4.

während die durch V_x bedingten Schubspannungen in dem gewöhnlichen, auch hier vorausgesetzten Falle, daß letztere in der Achsschicht am größten sind, erfordern:

Jb/S₀ = V_x/τ

5.

(über J, W s. Bd. 1, S. 794).

[542] Nach diesen Gleichungen wären z.B. im Falle von Fig. 7

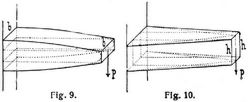
Es sind also die aus 4. mit Rücksicht auf M_x berechneten Dimensionen jedenfalls nur so lange verwendbar, als nicht aus 5. mit Rücksicht auf V_x ungünstigere Werte folgen, weshalb in der für das Lexikon berechneten Tabelle S. 541 die aus 4. und 5. folgenden Werte angegeben sind. Selbstverständlich lassen sich Näherungsformen bilden, welche beiden Bedingungen genügen, wie solche z.B. Fig. 9 und 10 für den Fall der Fig. 4 bei konstantem b und h darstellen. Die den M_x und V_x allein entsprechenden Dimensionen sind durch punktierte Linien angedeutet.

Da die Formeln 4., 5. auf der Voraussetzung gerader Stäbe mit horizontaler Achse beruhen, so sind die berechneten Querschnitte so anzuordnen, daß die Achsschicht eine horizontale Symmetrieebene bildet, was bei rechteckigem Querschnitt von konstantem b häufig unberücksichtigt bleibt, indem man die obere oder untere Begrenzungsfläche des Stabes horizontal wählt.

Die Untersuchungen, betreffend Körper von gleichem Widerstande, gehören zu den ältesten der Elastizitäts- und Festigkeitslehre. Bereits Parent, der 1713 zuerst die richtige Lage der neutralen Schicht horizontaler Balken erkannte, hatte sich in einigen Aufsätzen von 1704–1710 mit der Bestimmung »d'autant qu'on veut des figures d'égale résistance« beschäftigt. Auch Eytelwein behandelte in seiner Statik fester Körper 1808 (Bd. 2, S. 267, 335) eine Reihe von Fällen, wobei er noch, wie Galilei, die neutrale Schicht horizontaler Balken durch deren untere Grenze legte und die Normalspannungen in allen Elementen eines Querschnitts gleich groß annahm. Mit Navier [1] fand die übliche Behandlungsweise von Balken auf Grund von M_x, σ Eingang. Im Brückenbau und Hochbau hat man sich Trägern gleichen Widerstands durch Fachwerke zu nähern gesucht und ist damit z.B. bei konstanten Gurtungsquerschnitten auf die Paulischen Träger gekommen (s.d. und [2]). Auch bei Pfeilern, Talsperren, Türmen (Eiffelturm) spielen Formen möglichst gleichen Widerstands eine Rolle, wenn der Materialaufwand verringert werden soll, wie überhaupt eine Ingenieurkonstruktion in statischer Beziehung dann am vollkommensten dimensioniert wäre, wenn an allen Stellen gegen alle Zerstörungsarten die gleiche Sicherheit bestünde (vgl. Dimensionenberechnung). Doch ist dies nie vollständig erreichbar.

Literatur: [1] Navier, Résumé des leçons sur l'application de la mécanique, Paris 1826, S. 270. – [2] Kopeke, Ueber Träger von gleichem Widerstande, insbesondere die Anwendung derselben zu Brücken durch Laves und Pauli, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1858, S. 292. – [3] Winkler, Die Lehre von der Elastizität und Fertigkeit, Prag 1867, S. 41, 71, 80, 82, 83, 86, 88, 101, 103, 110, 163. – [4] Renoust des Orgeries, Mémoire sur les poutres droites, Annales des ponts et chaussées 1871, II, S. 170. – [5] Weisbach, Lehrbuch der theoretischen Mechanik, Braunschweig 1875, S. 398, 536, 608. – [6] Grashof, Theorie der Elastizität und Fettigkeit, Berlin 1878, S. 44, 113, 131. – [7] v. Ott, Vorträge über Baumechanik, II, Prag 1880, S. 30, 138, 143, 149, 152. – [8] Léauté, Sur les solides d'égale résistance, Compt. rend. 1882, XCV, S. 1219. – [9] Ritter, A., Lehrbuch der technischen Mechanik, Leipzig 1884, S. 508, 542. – [10] Collignon, Cours de mécanique appliquée aux constructions, I, Paris 1885, S. 123, 131, 287, 421. – [11] Levy, La statique graphique et ses applications aux constructions, IV, Paris 1888, S. 197 (Fachwerke). – [12] Koenen, Ueber ringförmige Stäbe und Platten gleichen Widerstandes, Zentralblatt der Bauverwaltung 1888, S. 118. – [13] Tetmajer, Die angewandte Elastizitäts- und Festigkeitslehre, Leipzig und Wien 1904, S. 236, 487. – [14] Bach, Elastizität und Fettigkeit, Berlin 1905, S. 210. – Die meisten Lehrbücher über Festigkeitslehre behandeln einige Fälle der Körper von gleichem Widerstande.

Weyrauch.

Fig. 1., Fig. 2., Fig. 3.

Fig. 4., Fig. 5., Fig. 6., Fig. 7., Fig. 8.

Fig. 9., Fig. 10.