- Parabolische Bewegung
Parabolische Bewegung eines Punktes ist diejenige, deren Beschleunigung nach Größe und Richtung konstant ist, ohne daß deren Geschwindigkeitsrichtung mit der Beschleunigungsrichtung zusammenfällt.
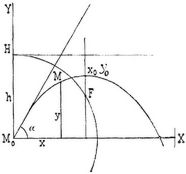
Sie tritt z.B. ein bei einem schweren Punkt, der unter einem Winkel α gegen die Horizontale in die Höhe geworfen wird. Für die Horizontale der Anfangslage M0 (s. die Figur), welche die Projektion der anfänglichen Geschwindigkeitsrichtung auf den Horizont ist, als; x-Achse und die aufwärts gerichtete Vertikale derselben als y-Achse sind die Gleichungen der parabolischen Bewegung
wo g die konstante Beschleunigung z.B. der Schwere ist, und es folgt aus ihnen, wenn
[24] die Koordinaten und die Komponenten der Geschwindigkeit zur Zeit t = 0 sind, allgemein für die Zeit t:
Demnach ist 1. die Bewegung eine ebene (z = 0), erfolgend in der Vertikalebene der Anfangsgeschwindigkeit. 2. Die Geschwindigkeit vy der Vertikalprojektion der Bewegung ist Null zur Zeit t = b : g und hierfür wird x0 = a b : g, y0 = 1/2b2 : g, welches die Koordinaten des höchsten Punktes sind, den der bewegliche Punkt erreicht (Scheitel der Bahn). 3. Verlegt man den Ursprung des Koordinatensystems in diesen Scheitel und kehrt den Sinn der y-Achse um, so wird die Gleichung der Bahn x2 = (2a2/g)y. Demnach ist die Bahn eine Parabel vom Parameter a2 : g und vertikaler Hauptachse. 4. Da die Directrix der Parabel um den halben Teil des Parameters vom Scheitel absteht, so ist die Höhe h der Directrix über die Anfangslage
wenn v0 die Anfangsgeschwindigkeit ist, deren Komponenten a = v0 cos α, b = v sin α sind, h ist unabhängig von α, daher haben alle Bahnen des Punktes, die den verschiedenen Werten von a entsprechen, dieselbe Directrix. Sie liegt in einer Höhe h über der Anfangslage M0, bis zu welcher der bewegliche Punkt mit der Anfangsgeschwindigkeit v0 würde vertikal aufsteigen können.
5. Für die Geschwindigkeit v als Funktion von t ergibt sich v2 = vx2 + vy2 = a2 + (b – g t)2 oder mit Rücksicht y = b t – 1/2g t2 auch: v2 = 2g(h – y). Die Geschwindigkeit v ist daher so groß als die eines Punktes, der von der Directrix bis zur Bahnstelle heruntergefallen wäre.
6. Die Wurfweite w ist die doppelte Abszisse des Scheitels
Sie wird ein Maximum für α = 1/4π. 7. Die Flugzeit t0, während der die Horizontalprojektion des beweglichen Punktes die Wurfweite mit der konstanten Geschwindigkeit a zurücklegt, ist:
also dem Sinus des Elevationswinkels α proportional. 8. Eliminiert man t zwischen den Gleichungen
ein, so erhält man die Gleichung; x2sec2 α – 4h tg α · x + 4h y = 0, mit Hilfe deren man den Winkel α finden kann, unter dem der Punkt von M0 aus geworfen werden muß, um einen bestimmten Punkt x y zu treffen. Diese Gleichung zweiten Grades zeigt, daß derselbe im allgemeinen durch zwei verschiedene Würfe erreichbar ist, einen steilen und einen flachen Wurf. Die Anfangslage M0 befindet sich auf allen möglichen Bahnen. Da diese alle eine gemeinsame Directrix haben, so liegt M0 von allen Brennpunkten um die Strecken h ab, und die Brennpunkte sämtlicher Bahnen liegen daher auf einem um die Anfangslage M0 mit h als Radius beschriebenen Kreise. 10. Die Koordinaten des Scheitels x = a b : g, y1/2b2 : g gehen durch Einführung von α und h über in x = h sin 2α, y = h sin 2α. Die Elimination von α zeigt, daß die Scheitel aller parabolischen Bahnen auf einer Ellipse liegen, deren Hauptachsen vertikal und horizontal sind und die Länge 2h und h haben, so daß die Mitte von h der Mittelpunkt derselben ist. 11. Soll ein Punkt M auf einer Geraden M0G getroffen werden, so findet man die Brennpunkte der beiden Parabeln, die durch ihn hindurchgehen, als die Durchschnitte eines um M beschriebenen, die gemeinsame Directrix aller Parabeln berührenden Kreises mit dem Ort der Brennpunkte. Der entfernteste Punkt M auf M0G, der noch erreichbar ist, wird erhalten als der Mittelpunkt M eines Kreises, der den Ort der Brennpunkte berührt. Für ihn fallen die beiden Brennpunkte und mithin auch die beiden durch ihn hindurchgehenden Parabeln zusammen. Er liegt daher auch auf der Enveloppe aller Parabeln. Er ist aber von M0 ebenso weit entfernt als von einer horizontalen Geraden H' G', die von M0 um 2 h absteht. Daher hüllen die sämtlichen Parabeln eine große Parabel ein, deren Brennpunkt M0, deren Parameter 4 h und deren Achse die Vertikale von M0 ist. 12. Die Koordinaten eines zur Zeit t = 0 auf irgendeiner der Parabeln von M0 ausgegangenen Punktes haben zur Zeit t die Werte x = v0 cos α · t, y = v0 sin α · t – 1/2 g t2. Eliminiert man hieraus α, so ergibt sich als Ort aller Punkte, welche zur Zeit t = 0 nach den verschiedensten Richtungen ausgegangen sein können, der Kreis x2 + (y + 1/2g t2) = (v0t)2, d.h. alle Punkte, die von M0 zu gleicher Zeit ausgehen, liegen zu jeder Zeit auf einem Kreise, dessen Radius der Zeit proportional wächst und dessen Mittelpunkt vertikal niedersinkt wie ein schwerer Punkt. 13. Läßt man die Ebene der Figur um die Vertikale von M0 rotieren, so erzeugt die Parabel, die alle Bahnen einhüllt, ein Rotationsparaboloid und der zuletzt genannte Kreis eine Kugelfläche. Man erhält das Phänomen einer idealen Fontäne.
Literatur: Tait und Steele, Treatise on dynamics of a partie, Bd. 6, London 1889, worin das vorliegende Problem auch synthetisch gelöst ist; Schell, Theorie der Bewegung und der Kräfte, 2. Aufl., Leipzig 1879, Bd. 1, S. 360–368.
(† Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.