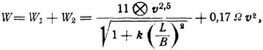Schiffswiderstand

Schiffswiderstand (vgl. a. Probefahrt). Die älteren Formeln zur Bestimmung des Schiffswiderstandes gehen teilweise von der Verdrängungstheorie aus – Formeln von Campaignac, Bourgeois, Dupuy de Lome, Nyström [7], Mansel, Thornycroft, Middendorf, Riehn, Afonassief u.a. –, teilweise. von der Stromlinientheorie – Formeln von Rankine, Kirk, Froude, Tidemann [5], Rauchfuß [8] u.s.w. – und geben meist direkt die Werte der erforderlichen Maschinenleistung in indizierten Pferdestärken. S.a. Kanalschiffahrt, Modellschleppstation.

Die Formel von Campaignac, JHP = ⊗ V³ : C, worin JHP die Größe der indizierten Pferdestärken, V die Geschwindigkeit des Schiffes in Knoten, ⊗ das Areal des Hauptspants in Quadratmetern und C eine Konstante, nach neueren Probefahrten zwischen 36 und 80 bedeuten, findet bei überschlägigen Berechnungen unter Benutzung der Werte von C ähnlicher Schiffe vielfach Verwendung; ebenso die ähnliche französische Formel JHP = ⊗ V³ : m³, worin m zwischen 3,4 und 4,0 schwankt, sowie die englische Admiralitätsformel JHP = V³ P²/₃ : C¹, worin P das Deplacement in engl. Tons (1 t = 1016 kg) bedeutet und C₁ zwischen 100 und 260 liegt. – Die Formeln von Riehn und Middendorf [1], [2], [9] geben gute Resultate, da sie bereits Rücksicht nehmen auf die Schiffsform, das Verhältnis von Länge zur Breite, die Völligkeit des Deplacements sowie die benetzte Oberfläche. Die ältere Middendorfsche Formel setzt sich aus dem Formwiderstand W₁ und dem Reibungswiderstand W₂ zusammen und lautet:

worin L die Länge des Schiffes zwischen den Perpendikeln in Metern, B die größte Breite in Metern, v die Geschwindigkeit in Metern pro Sekunde, Ω die benetzte Oberfläche in Quadratmetern und k ein Koeffizient ist, der sich nach dem Völligkeitsgrade des Deplacements richtet und im allgemeinen gleich 2 zu setzen ist. Die Bestimmung der indizierten Pferdestärken ergibt sich aus der Formel

worin a die Kreisfläche der Schraube bezw. die Fläche zweier Radschaufeln in Quadratmetern und η der Wirkungsgrad der Maschine ist (0,6 bei kleineren Maschinen bis 0,9 bei hohen Pferdestärken). Die neue Formel von Middendorf legt Schiffsformen zugrunde, welche mit der geforderten Geschwindigkeit in besserem Einklang stehen, auch ist mit einer besseren Beschaffenheit der benetzten Oberfläche gerechnet. Sie lautet:

Der Wert von ε ist abhängig von L : v², der von k von L : B. Die Rankinesche Formel berücksichtigt neben der benetzten Oberfläche Ω den mittleren Neigungswinkel α aller Wasserlinien im Bug gegen die Längsschiffsachse und ist J HP = V³ Ω(1 + 4 sin² α + sin⁴α) : 20000, wobei V in Knoten und Ω in Fuß engl. angegeben ist. Die Ziffer 20000 sinkt bei völligen Schiffen bis auf 16000.

Eine Vereinfachung der Rankineschen Formel bildet die von Kirk, bei welcher die umständliche Berechnung der benetzten Oberfläche durch die Berechnung der Oberfläche eines Blockmodells ersetzt wird von der Länge des Schiffes mit parallelepipedischem Mittelschiff und dreiseitig prismatischen zugespitzten Enden; es kommen bei diesem Blockmodell auch die Eintrittswinkel im Vor- und Hinterschiff in Betracht. Für die Bestimmung der indizierten Pferdestärken nimmt Kirk nach praktischen Versuchen an, daß für je 100 Quadratfuß engl. bei einer Geschwindigkeit von 10 Knoten 5 PS_i für gewöhnliche und 4 PS_i für scharfe Schiffsformen erforderlich sind. Für eine Blockmodelloberfläche von 15000 Quadratfuß und 15 Knoten Geschwindigkeit wird demnach JHP = (15 : 10)³ ∙ 5 ∙ 150 = 2531 [1], [2], [6].

[692] Die Formel von Froude beruht auf der Feststellung des Schiffswiderstandes durch Schleppversuche an Modellen nach dem von ihm durch Schleppversuche im großen und an Modellen aufgehellten sogenannten Gesetz der korrespondierenden Geschwindigkeiten. Verhalten sich die linearen Dimensionen des Modells zu jenen des Schiffes wie 1 : n und sind die beobachteten Modellwiderstände bei den Geschwindigkeiten von v₁ v₂ v₃, r₁ r₂ r₃ u.s.w., so sind die Widerstände des Schiffes bei den Geschwindigkeiten v√n, v₁√n, v₂√n gleich n³ r, n³ r₁, n³ r₂ u.s.w. Froude bezeichnet die Geschwindigkeiten v und v√n, v₁ und v₁√n u.s.w. als korrespondierende Geschwindigkeiten. Trägt man nun bei den verschiedenen Geschwindigkeiten des Modells als Abszissen die beobachteten Widerstände als Ordinaten auf, so ergibt sich die Widerstandskurve des Modells. Nach weiteren Versuchen von Froude hat sich nun ergeben, daß die Reibungswiderstände von Schiff und Modell erheblich differieren und daß im besonderen die Reibung mit zunehmender Länge der Reibungsfläche abnimmt. Der Reibungswiderstand berechnet sich hiernach aus Wr = k γ Ω v^m, worin γ das spezifische Gewicht des Wassers ist, während k und m nach der Länge der Reibungsfläche von 0,22–0,15 bezw. von 1,9–1,83 variieren. – Ermittelt man demnach nach dieser Formel für die einzelnen Geschwindigkeiten die Kurve des Reibungswiderstandes des Modells, so ergibt die Differenz zwischen dieser Kurve und der Gesamtwiderstandskurve die Größen des form- und weltenbildenden Widerstands des Modells, welche dann nach dem Gesetz der korrespondierenden Geschwindigkeiten zu einer Kurve des form- und weltenbildenden Widerstandes des Schiffes übertragen werden können. Trägt man auf diese Kurve als Ordinaten die einzelnen Reibungswiderstände des Schiffes, für die größere Schiffslänge berechnet, hinzu, so ergibt die so erzielte Kurve die Gesamtwiderstandskurve des Schiffes für die korrespondierenden Geschwindigkeiten. Mit Hilfe der Modellschleppversuche ist man daher imstande, für eine bestimmte geforderte Maximalgeschwindigkeit diejenige Schiffsform durch Versuche mit verschiedenen Modellen zu ermitteln, welche den geringsten Widerstand erfordert. Um ferner über die Form des Propellers für sich sowie mit Bezug auf die Schiffsform Aufschluß zu erhalten, werden zu gleicher Zeit Schleppversuche mit verschiedenen Propellerformen gemacht, wobei dieselben in entsprechende Umdrehungen versetzt werden, so daß man mit Hilfe der Schleppversuche auch den Effektverlust der Propeller durch Slip, Reibung, Wirbelbildung mit großer Genauigkeit vorausbestimmen kann. Tanks zur Vornahme von Modellschleppversuchen sind zurzeit bei allen größeren Marinen und Schiffswerften vorhanden, und die Versuche tragen wesentlich zur Klärung der Gesetze des Schiffswiderstandes bei ([2]–[6], [10], [12]). Neuerdings ist die Schleppmethode durch das System Wellenkamp (s. Modellschleppstation) wesentlich vereinfacht, und ergeben die automatisch aufgezeichneten Geschwindigkeitsmessungen bei konstantem Zuggewicht eine erheblich größere Genauigkeit [13].

Literatur: [1] Krieger-Johows Hilfsbuch für den Schiffbau, Berlin 1902. – [2] Busley, C., Die Schiffsmaschine, Kiel 1886. – [3] Pollard u. Dudebout, Theorie du navire, Paris 1890–94. [4] Tullinger, Ueber Nutzen und Einrichtung von Stationen zum Schleppen von Schiffsmodellen, Mitteilungen aus dem Gebiet des Seewesens 1885. – [5] Dislère, Exposé sommaire des experiences faites à Amsterdam sur la résistance des carènes, Paris 1879. – [6] Rota, G., La Vasca per le esperienze di architettura navale nel R. Arsenale di Spezia, Genua 1889. – [7] Nyström, Pocket book of Mechanics, Philadelphia 1882. – [8] Rauchfuß, Ueber den Schiffswiderstand, Berlin 1880. – [9] Riehn, Die Berechnung des Schiffswiderstandes, Hannover 1882. – [10] Taylor, Resistance of ships and screw propulsion, New York 1907. – [11] Middendorf, Widerstand der Schiffe und Ermittlung der Arbeitsleistung für Schiffsmaschinen, Jahrbuch der Schiffbautechn. Gesellschaft, Berlin 1900. – [12] Schütte, Die Schleppversuchsstation des Norddeutschen Lloyd, Zeitschr. Schiffbau 1900. – [13] Wellenkamp, Eine neue Modellschleppmethode, Jahrbuch der Schiffbautechn. Gesellschaft, Berlin 1908.

T. Schwarz.