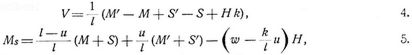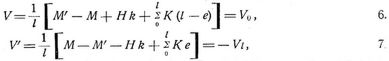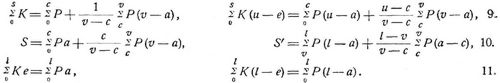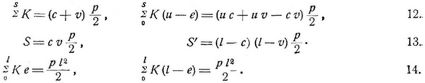Schnittkräfte, Schnittmomente

Schnittkräfte, Schnittmomente. Infolge Einwirkung äußerer Kräfte (s.d.) und andrer Ursachen entstehen bei allen Körpern innere Kräfte, mit welchen die Teile zu beiden Seiten beliebiger durch die Körper gedachter Schnitte aufeinander wirken. Die Kräfte, mit welchen dies geschieht, heißen Schnittkräfte (vgl. Druck, Bd. 3, S. 111), ihre Momente in Hinsicht gegebener Punkte Schnittmomente und die Beanspruchungen pro Flächeneinheit durch dieselben Spannungen (s.d.). Die Querschnittskräfte und Biegungsmomente stabförmiger (vollwandiger) Träger (s.d.) sind besondere Fälle der Schnittkräfte und Schnittmomente (s. Angriffsmoment, Balken, Bogen u.s.w.), doch spielen letztere auch eine Rolle bei der Berechnung von Fachwerken und Gitterträgern (Bd. 3, S. 546, 549; Bd. 4, S. 536); im folgenden sind sie für beliebige ebene Träger mit nur vertikalen Aktivkräften (Lasten) ausgedrückt. Für beliebig gerichtete Lasten in der Trägerebene s. [2], Aufg. 4, 5; Beisp. 40, 58, 86.

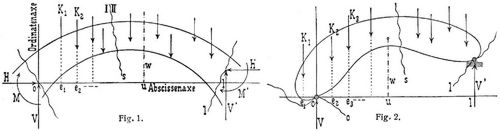
Man denke sich durch den Träger einen beliebig geformten Schnitt s gelegt (Fig. 1). Für die Kräfte, mit welchen der Trägerteil links von s auf den Trägerteil rechts von s wirkt, sei H_s die resultierende Horizontalkraft, V_s die resultierende Vertikalkraft, M_s das resultierende Moment in Hinsicht eines Drehpunkts der beliebigen Koordinaten u, w in der Trägerebene. Die Horizontalentfernung der links und rechts vom Schnitte s zunächst folgenden Stützpunkte werde durch l bezeichnet. Wir wählen den Stützpunkt links als Ursprung eines rechtwinkligen[769] Koordinatensystems in der Trägerebene mit horizontaler Abszissenachse und vertikaler Ordinatenachse, für den Stützpunkt rechts sind l, k die Koordinaten. Durch die Stützpunkte 0 und l denken wir uns beliebig geformte Schnitte 0 und l gelegt. H sei der Wert von H_s im Schnitte s = 0, während V und – V' die Werte von V_s für s = 0 und s = l bedeuten und M, M' die Momente M_s für s = 0 mit u = 0, w = 0 bezw. für s = l mit u = l, w = k.

Zwischen den Schnitten 0 und l mögen bei den Abszissen e₁ e₂ ... beliebige Lasten K₁, K₂ ... (bei Fachwerken Knotenpunktslasten) auf den Träger kommen. Dann hat man im beliebigen Schnitt s, [1], S. 19:

Mit den Bezeichnungen

kann man auch schreiben:

während weiter gelten:

unter V₀, V_l die Werte von V_x für x = 0 und l verstanden. Durch Addition von 6. und 7. folgt:

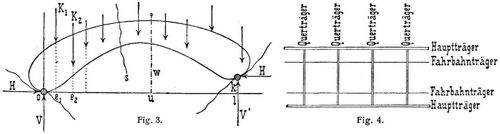
Die Summe der Vertikalreaktionen gegen einen Trägerteil ist gleich der Belastung desselben. Die erste Gleichung 1. besagt: Hat ein Träger nur Lasten aufzunehmen (keine horizontalen Aktivkräfte, s.d.), dann ist die Horizontalkraft für alle beliebig geformten Schnitte durch eine Oeffnung desselben gleichgroß. In 1.–8. bedeuten die Grenzen der Summen Σ Schnitte, also nur bei vertikalen Schnitten gleichzeitig Abszissen. In dem gewöhnlichen Falle gleich hoher Stützpunkte ist in obigen Gleichungen k = 0, für einfache und durchlaufende Balken (s.d.) einschließlich der Balkenfachwerke (s.d.) ist H_s = H = 0, für Balken und Bogen mit zwei Gelenkauflagern (Fig. 2, 3) sind M = 0, M' = 0. [1], S. 21.

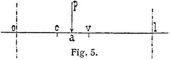
Bei Brücken wirken die Verkehrsarten meist nicht direkt auf die Hauptträger, sie werden durch ein System von Zwischenträgern (Längsträger oder Fahrbahnträger und Querträger, z.B. nach der Anordnung Fig. 4) in bestimmten Knotenpunkten auf die Hauptträger übertragen. Es sind also die. Knotenpunktslasten K nicht unmittelbar gegeben. Bei ihrer Ableitung pflegen alle Zwischenträger als gewöhnliche Balken mit zwei Gelenkauflagern (Bd. 1, S. 519) betrachtet zu werden. Es mögen nun beliebige Verkehrslasten P₁, P₂, ... bei Abszissen a₁, a₂, ... zunächst auf die Fahrbahn wirken, c und v seien die Abszissen derjenigen Knotenpunkte, bei welchen der von Schnitt s getroffene Fahrbahnträger aufliegt (Fig. 5). Dann sind die von den Verkehrslasten P herrührenden Werte der Summenausdrücke Σ in obigen Gleichungen für beide durch die Querträger verbundenen Hauptträger [1], S. 26:

[770] Speziell für eine auf die ganze Spannweite l gleichmäßig verteilte Last von p pro Längeneinheit hat man einfacher:

Für 9.–14. ist vorausgesetzt, daß auch bei 0 und l Querträger oder doch Auflager von Längsträgern liegen. Bei stabförmigen (vollwandigen) Trägern werden die Schnitte s als Querschnitte x und die Drehpunkte der Momente in den Achspunkten der Querschnitte angenommen. Setzt man demgemäß s = x, u = x, w = y, so entstehen aus 1.–8. die für stabförmige Balken- und Bogen gültigen Formeln (vgl. Bd. 1, S. 503; Bd. 2, S. 141). – Ueber die Grenzwerte der Schnittkräfte und Schnittmomente bei veränderlicher Belastung s. Grenzwerte, Einflußlinien. Ausdrücke für die häufig allein interessierenden Momente M_s und ihre Grenzwerte bei gleichmäßig verteilter bewegter Last und bewegten Radlastzügen [1] §§ 23–25 (einfache Balkenfachwerke u.s.w.), §§ 57–59 (durchlaufende Gelenkträger), §§ 66–68 (Bogenfachwerke u.s.w. mit drei Gelenken), §§ 76, 78, 80–82, 85 (verschiedene Träger).

Literatur: [1] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887. – [2] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888.

Weyrauch.

Fig. 1., Fig. 2.

Fig. 3., Fig. 4.

Fig. 5.