- Sprengwerke
Sprengwerke. Wie der Namen Hängwerk (Bd. 4, S. 732) so wurde auch die Bezeichnung Sprengwerk im Ingenieurwesen verschieden verwendet [7]. Allgemein jedoch hat man Konstruktionen nach Art von Fig. 1 und 2 einfaches und doppeltes Sprengwerk genannt. Bei diesen ist ein gewöhnlicher einfacher Balken (Bd. 1, S. 519) durch schief nach aufwärts gerichtete Streben, zwischen welchen beim doppelten Sprengwerk der horizontale Spannriegel liegt, unterstützt und damit verstärkt. Der Balken wirkt dann als durchlaufender Balken (Bd. 1, S. 505, 507) mit nachgiebigen Zwischenstützen, während die darunter liegenden Stäbe des Sprengbocks gedrückt werden. Die bei der Berechnung solcher Sprengwerke üblichen Voraussetzungen sind aus der Andeutung der Gelenke und Gleitungen in Fig. 3, 4 ersichtlich (s. a. Träger), doch kann das feste Gelenkauflager des Balkens ohne Aenderung der folgenden Beziehungen auch an eine Zwischenstütze gelegt werden. Vorausgesetzt ist, daß der Balken immer mit sämtlichen Auflagern in Berührung bleibt.
Greifen beliebige Lasten P1, P2 ... in Entfernungen a1, a2, ... vom Auflager 0 des Balkens an, so würden für den einfachen Balken (ohne Unterstützung durch den Sprengbock), die Stützenreaktionen bei 0 und l:
und das Moment und die Vertikalkraft in einem beliebigen Querschnitt x (in Entfernung x) vom Auflager 0):
worin wie in der Folge die Summen Σ alle Latten zwischen den beigesetzten Grenzen umfassen. Ueber ihre Werte für stetig verteilte Latten s. Belastung der Träger, Bd. 1, S. 661. Für eine auf die ganze Spannweite l gleichmäßig verteilte Last von u pro Längeneinheit beispielsweise hat man:
Infolge der hinzukommenden Unterstützung durch den Sprengbock, welcher den Druck 2 X aufnimmt, werden die wirklichen Reaktionen der Endstützen des Balkens:
R = V – X, R' = V' – X,
4.
sowie der Horizontalschub und die Beanspruchungen der Streben, und in Fig. 4 des Spannriegels:
H = X d/h, Y = – X b/h, Z = – H.
5.
Für die Streben und den Spannriegel sind b, c die Längen, B, C die Querschnitte, Ey, Ez die Elastizitätsmoduln, αy, αz die (linearen) Ausdehnungskoeffizienten, während E, J Elastizitätsmodul und Trägheitsmoment des Balkens bedeuten. Die Größe X war aus der Elastizitätslehre zu berechnen, wozu eine Gleichung aus dem Art. »Träger, zusammengesetzte«, verwendet wurde.
Einfaches Sprengwerk. Fig. 3. Mit l = 2 k und der abkürzenden Bezeichnung erhält man durch beliebige Belastung:
m = l3 μ = l3 (1 + 24 E J b3/B Ey h2 l3)
6.
erhält man durch beliebige Belastung:
wonach beispielsweise für eine auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit:
X = 5 ul/16 μ
8.
[228] für verschiedene gleichmäßig verteilte Latten von u, u' auf der ersten und zweiten Hälfte der Spannweite:
X = 5 (u + u')l/32 μ,
9.
und für eine Einzellast P inmitten der Spannweite:
X = P/2μ.
10.
Durch eine Temperaturänderung τ der Streben (gegen die dem spannungslosen Zustande entsprechende Normaltemperatur) entsteht:
X = αy τ/m h 24 E J b2,
11.
während eine gleichmäßige Temperaturänderung des Balkens keine Beanspruchung erzeugt. – Für das Moment und die Vertikalkraft in den Querschnitten x des unterstützten Balkens hat man allgemein:
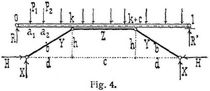
Doppeltes Sprengwerk. Fig. 4. Mit l = 2 k + c und der abkürzenden Bezeichnung
ergibt sich für beliebige Belastung:
wonach für eine auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit:
X = u/2 n k (k + c)(5 k2 + 5 k c + c2),
16.
durch verschiedene gleichmäßig verteilte Lasten von u, u' pro Längeneinheit auf der ersten und zweiten Balkenhälfte:
X = u + u'/4 n k (k + c) (5 k2 + 5 k c + c2),
17.
für verschiedene gleichmäßig verteilte Lasten u, u', u'' von 0 bis k bezw. von k bis k + c und von k + c bis l:
X = u + u''/4 n k3 (5 k + 6 c) + u'/2 n k c (4 k2 + 6 k c + c2),
18.
durch eine bei k oder k + c angreifende Last P und durch zwei bei k und k + c angreifende Lasten P2, P2:
X = P/2 v (v s. Gleichung 14.) bezw. X = P1 + P2/2 v
19.
durch Temperaturänderungen τy, τz der Streben bezw. des Spannriegels:
X = 6 E J/n h (2 αy τy b2 + αz τz d).
20.
Eine gleichmäßige Temperaturänderung des Balkens ist ohne Einfluß auf die Beanspruchungen. Das Moment und die Vertikalkraft in den Querschnitten x des unterstützten Balkens sind allgemein:
Nach vorstehenden Gleichungen lassen sich die Beanspruchungen der betrachteten Sprengwerke berechnen, sobald die Querschnitte bekannt sind. Zur vorläufigen Ermittlung der letzteren und andern Näherungsrechnungen können dieselben Gleichungen dienen: beim einfachen Sprengwerk mit m = l3 μ = 1, beim doppelten Sprengwerk mit n = 2 k2 (2 k + 3 c), v = 1, welche Werte unnachgiebigen Zwischenstützen entsprechen (Ey = ∞, Ez = ∞ in 6., 14.). Ueber die Grenzbeanspruchungen bei bewegter Last s. Grenzwerte, Bd. 4, S. 626.
Literatur: [1] Fränkel, Theorie des einfachen Sprengwerks, Civilingenieur 1876, S. 22. – [2] Melan, Theorie des Sprengwerks, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1876, S. 233. – [3] Steiner, Kontinuierliche Träger mit balancierten Stützen, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1876, S. 245 (s.a. Wochenschr. d. Vereins 1887, S. 37, 42, 107, und Techn. Blätter 1885, S. 157, und 1890, S. 212). – [4] Holzhey, Vorträge über Baumechanik, II, Wien 1879, S. 777. – [5] Winkler, Theorie der Brücken, I, Aeußere Kräfte der Balkenträger, Wien 1886, S. 233, 255. – [6] Hoch, Berechnung doppelter Hänge- und Sprengwerke bei einseitiger Belastung, Zentralblatt d. Bauverwaltung 1888, S. 474. – [7] Lang, Zur Entwicklungsgeschichte der Spannwerke des Bauwesens, Riga 1890, S. 3, 12, 28. – [8] Müller-Breslau, Die neueren Methoden der Festigkeitslehre und der Statik der Baukonstruktionen, Leipzig 1904, S. 106, 110. – [9] Horowitz, Beitrag zur praktischen und einfachen Berechnung der Häng- und Sprengwerkkonstruktionen, Techn. Blätter 1904, S. 41, 160. – [10] Reich, Die günstigste Anlage eines Trapezsprengwerkes, Rundschau f. Technik und Wirtschaft 1908, S. 97. – [11] Moser, Ueber doppelte Sprengwerke, Schweiz. Bauztg. 1908, LII, S. 129. – [12] Hartmann, Ueber armierte und Sprengwerkträger mit exzentrischem Strebenanschluß, Zeitschr. d. Oesterr. Ing.- u. Arch.-Vereines 1908, S. 517, 533. – [13] Müller-Breslau, Die graphische Statik der Baukonstruktionen, II 2, Leipzig 1908, S. 341.
Weyrauch.
http://www.zeno.org/Lueger-1904.