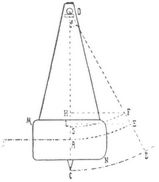
- Ballistisches Pendel
Ballistisches Pendel (erfunden von Benjamin Roberts 1740). Dasselbe ist ein schweres, um eine horizontale Achse drehbares Pendel, gegen das eine Geschützkugel abgeschossen wird, um die Geschwindigkeit zu bestimmen, mit der dieselbe das Rohr verläßt.
Es sei (s. Figur) S der Schwerpunkt des Pendels, dessen unterer Körperteil MN aus einem mit Erde gefüllten Karten besteht und in den die Kugel in der Richtung K A eindringt und dadurch das Pendel nötigt, sich um einen gewissen Ausschlagwinkel α um seine horizontale Achse O zu drehen. Ist ν die Geschwindigkeit, mit der eine Kugel von der Masse m eindringt, u die Geschwindigkeit derselben am Ende des Stoßes, von wo sie mit dem Pendel zusammen ein System bildet, F aber die sie treibende Kraft, so hat man nach dem Satze über die Bewegungsgrößen (oder Momentankräfte)
oder wenn f der Mittelwert von F während der Stoßzeit ϑ ist,
m(v – u) = fϑ.
Durch diese Momentanwirkung wird das System eine gewisse Winkelgeschwindigkeit ω um die Achse O erlangen, und zwar ist
Mk2 = lfϑ oder Mk2ω = ml(v – u),
wenn M die Gesamtmasse, k der Trägheitsradius um die Achse O und O A = l ist. Hieraus folgt v = u + (Mlω)/m oder, da u = lω ist,
Bilden wir jetzt die Gleichung der lebendigen Kraft des Systems. Diese ist null, wenn dasselbe den Ausschlagwinkel α erreicht hat, und besteht zu Anfang aus der lebendigen Kraft Mk2ω2 des Pendels und ml2ω2 der Kugel; ihr Wert ist daher zu Anfang
(Mk2 + ml2)ω2.
Die Arbeit der Schwere am Pendel ist M g k, wenn h = a(1 – cosα) die Höhe SH bedeutet, auf die der Schwerpunkt gehoben wird; die Arbeit der Schwere an der Kugel ist – m g h', wo h'/h = l/a, also – m g h' = – m g l h/a wird. Demnach ist die Gesamtarbeit der Schwere
und wird die Gleichung der lebendigen Kraft
Diese Gleichung liefert in Verbindung mit
die Größen ω und v, deren letztere zu bestimmen die Aufgabe war. Es wird:
Damit die Achse O keine Erschütterungen erleide, welche die Genauigkeit der Beobachtung des Winkels α beeinträchtigen können, muß A der Schwingungspunkt des Pendels, d.h. O A = l die Länge des einfachen Pendels sein, das mit dem vorliegenden physischen Pendel gleiche Oszillationsdauer hat, nämlich l = a + (k20)/a, wo k0 der Trägheitsradius für die durch S zur Achse O parallel gelegte Achse ist. Den Winkel α beobachtet man mit Hilfe einer am tiefsten Teile des Pendels angebrachten Spitze.
Literatur: Cranz, C., Kompendium der theoretischen äußeren Ballistik, Leipzig 1896, S. 421.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.