Kegelschnitte

Kegelschnitte, Kurven zweiter Ordnung, welche von jeder Geraden in zwei Punkten geschnitten werden. Ein Kegelschnitt ist durch fünf Punkte bestimmt Die allgemeine Gleichung eines solchen ist: a₁₁ x² + 2a₁₂ x y + a₂₂ y² + 2a₁₃ x + 2a₂₃ y + a₃₃ = 0. Je nachdem der Kegelschnitt mit der unendlich fernen Geraden zwei komplex-konjugierte, zusammenfallende, reelle getrennte Punkte gemein hat, also je nachdem a₁₁ a₂₂ – a₁₂² 0 heißt er Ellipse, Parabel (apollonische Parabel), Hyperbel.

Allgemeines. Ist ξ η ein Punkt, der nicht dem Kegelschnitt angehört, so ist die Gerade

(a₁₁ ξ + a₁₂ η + a₁₃) x + (a₁₂ ξ + a₂₂ η + a₂₃) y + (a₁₃ ξ + a₂₃ η + a₃₃) = 0

der Ort der vierten harmonischen Punkte auf jedem Strahl durch ξ η zu diesem Punkt und den Schnittpunkten des Strahls mit dem Kegelschnitt. Die Gerade heißt Polare von ξ η in bezug auf den Kegelschnitt, dieser Punkt selbst ihr Pol. Die Polare jedes Punkts der Polare geht durch den Pol. Schneiden sich zwei Tangenten auf der Polare, so werden sie von dieser und der Verbindungslinie des Schnittpunkts mit dem Pol harmonisch getrennt. Zwei Punkte, von denen jeder auf der Polare des andern liegt, heißen konjugiert, ebenso zwei Gerade, von denen jede durch den Pol der andern geht. Ein Dreieck, dessen Ecken Pole ihrer Gegenseiten sind, heißt Polardreieck. Die Polare ist die Berührungssehne des von (ξ, η) an den Kegelschnitt gelegten Tangentenpaares mit der Gleichung:

(a₁₁ ξ² + 2a₁₂ ξ η, + ...) (a₁₁ x² + 2a₁₂ x y + ...) – (a₁₁ ξ x + a₁₂ [η x + ξ y] + ...)² = 0.

Ein Kegelschnitt kann erzeugt werden durch den Schnittpunkt zweier entsprechenden Strahlen in projektivischen Strahlenbüscheln oder auch nach Newton durch den Schnittpunkt je eines Schenkels von zwei Winkeln, deren Spitzen fest sind und deren andre Schenkel sich fortwährend auf einer Geraden schneiden. Verbindet man einen Punkt P des Kegelschnitts mit vier andern Punkten desselben, so ist das Doppelverhältnis der vier Strahlen von der Lage des Punktes P unabhängig. Satz von Maclaurin: Wenn die Seiten eines Dreiecks sich um feste Punkte drehen und zwei Ecken sich auf festen Geraden bewegen, so beschreibt der dritte Eckpunkt einen Kegelschnitt. Satz des Pappus: Ist einem Kegelschnitt ein Viereck einbeschrieben, so ist das Verhältnis des Produkts der Abstände eines Kegelschnittpunkts P von zwei Gegenseiten des Vierecks zum Produkt seiner Abstände von den beiden andern von der Wahl von P unabhängig. Satz von Desargues: Ist einem Kegelschnitt ein vollständiges Viereck einbeschrieben, so bilden die Schnittpunkte einer beliebigen Geraden g mit dem Kegelschnitt ein Punktepaar einer Involution, welche durch die Schnittpunkte von g mit je zwei Gegenseiten des Vierecks bestimmt ist. Satz von Pascal: Ist einem Kegelschnitt ein Sechseck einbeschrieben, so schneiden sich die drei Paare von Gegenseiten auf einer Geraden. Satz von Brianchon: Ist einem Kegelschnitt ein Sechseck umbeschrieben, so gehen die Verbindungslinien der drei Paare von Gegenecken durch einen Punkt. Satz von Carnot: Ist A B C ein Dreieck, dessen Seiten B C, C A, A B den Kegelschnitt resp. in den Punktepaaren A₁ A₂, B₁ B₂, C₁ C₂ schneiden, so ist:

A B₁ · A B₂ · B C₁ · B C₂ · C A₁ · C A₂ = A C₁ A C₂ · C B₁ · C B₂ · B A₁ · B A₂.

Der Pol der unendlich fernen Geraden in Beziehung auf den Kegelschnitt heißt Mittelpunkt desselben. Wird er als Ursprung gewählt, so ist in der allgemeinen Gleichung a₁₃ = a₂₃ = 0. Eine Gerade durch den Mittelpunkt heißt Durchmesser (s.d.). Zwei Durchmesser heißen konjugiert, wenn jeder durch den Pol des andern geht. Die einzigen zwei konjugierten Durchmesser, die aufeinander senkrecht stehen, heißen Hauptachsen, die Endpunkte derselben Scheitel, die Entfernungen der Scheitel vom Mittelpunkt Halbachsen. Werden die Hauptachsen zu Koordinatenachsen gewählt, so ist in der allgemeinen Gleichung a₁₂ = 0. Die beiden[421] imaginären Tangentenpaare, welche von den unendlich fernen Kreispunkten an den Kegelschnitt gehen, schneiden sich in vier Punkten, welche Brennpunkte genannt werden. Von denselben liegen zwei auf der einen (sogenannten kleinen) Hauptachse und sind imaginär; die beiden andern sind reell und liegen auf der andern (großen) Hauptachse symmetrisch zum Mittelpunkt. Ihre Entfernung von diesem heißt Exzentrizität. Die Polare eines Brennpunkts heißt Leitlinie oder Directrix (s.d.). 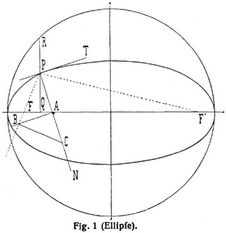Das Verhältnis der Abstände der Kegelschnittpunkte von einem Brennpunkt und der zugehörigen Directrix ist konstant, es ist 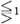bei der Ellipse, Parabel, Hyperbel. Eine Gerade durch den Brennpunkt heißt Leitstrahl, eine Sehne durch denselben Brennsehne. Zieht man von einem Kegelschnittpunkt die Leitstrahlen nach den beiden Brennpunkten, so wird der Winkel derselben durch die Normale resp. die Tangente halbiert. Die Strecke, welche auf einer beweglichen Tangente von zwei festen Tangenten begrenzt wird, erscheint, vom Brennpunkt aus gesehen, unter konstantem Winkel. Der Winkel, unter welchem eine Sehne vom Brennpunkt aus erscheint, wird von dem Leitstrahl durch ihren Pol halbiert. Zwei aufeinander senkrechte Leitstrahlen sind konjugierte Gerade in bezug auf den Kegelschnitt. Die Projektion der Normalen auf den Leitstrahl ist gleich der Ordinate des Brennpunkts (wenn die große Halbachse Abszissen-, die kleine Ordinatenachse); dieselbe heißt auch Halbparameter p und ist gleich der mittleren Proportionale aus den beiden Abschnitten, in welche eine beliebige Brennsehne durch den Brennstrahl geteilt wird. Konstruktion des Krümmungsmittelpunkts C für einen Punkt P des Kegelschnitts (Fig. 1): Ziehe die Normale P A bis zur großen Hauptachse, errichte auf derselben das Lot A B bis zum Leitstrahl F P (Brennpunkt), errichte auf B P das Lot B C bis zur Normale. Zwei Kegelschnitte, K = 0 und K' = 0, schneiden sich in vier Punkten, durch diese (Grundpunkte) geht ein Kegelschnittbüschel K + λ K' = 0. Die Kegelschnitte desselben schneiden jede Gerade in Punktepaaren einer Involution. Zu ihnen gehören drei Geradenpaare, die Gegenseitenpaare des von den Grundpunkten gebildeten vollständigen Vierseits. Die Diagonalpunkte desselben bilden ein Dreieck, das für alle Kegelschnitte des Büschels Polardreieck ist. Zwei Kegelschnitte berühren sich, wenn von ihren Schnittpunkten zwei zusammenfallen; sie oskulieren sich resp. berühren sich vierpunktig, wenn drei resp. vier Schnittpunkte zusammenfallen; sie stehen in doppelter Berührung, wenn die Schnittpunkte paarweise zusammenfallen. Zwei Kegelschnitte sind konfokal, wenn sie dieselben Brennpunkte besitzen. Zu zwei gegebenen Brennpunkten gehört eine Schar konfokaler Kegelschnitte. Von diesen gehen durch jeden Punkt der Ebene zwei, eine Ellipse und eine Hyperbel, die sich rechtwinklig durchschneiden. Ist ein einfach-unendliches System von Kegelschnitten durch vier Bedingungen gegeben, so nennt man Charakteristiken die Zahl μ der Systemkurven, die durch einen gegebenen Punkt gehen, und die Zahl ν der Systemkurven, welche eine gegebene Gerade berühren. Beispiel: Für das Kegelschnittsystem, welches vier gegebene Geraden berührt, ist μ = 2; ν = 1. Näheres s. [4], S. 390 ff.

Diskussion der allgemeinen Kegelschnittsgleichung:

Mit

wird:

I. Δ =|= 0 (eigentliche Kegelschnitte). 1. A₃₃ > 0 Ellipse a) a₁₁ und Δ haben gleiche Vorzeichen: imaginäre Ellipse (kein reeller Punkt); b) a₁₁ und Δ haben verschiedene Vorzeichen: reelle Ellipse (speziell a₁₁ = a₂₂; a₁₂ = 0 Kreis). 2. A₃₃ = 0 Parabel. 3. A₃₃ < 0 Hyperbel.

II. Δ = 0 (zerfallende Kegelschnitte). 1. A₃₃ =|= 0 Geradenpaare; a) A₃₃ > 0 imaginäres Geradenpaar; b) A₃₃ < 0 reelles Geradenpaar. 2. A₃₃ = 0 Doppelgerade.

Die Ellipse besitzt keine reellen unendlich fernen Punkte; sie ist eine in bezug auf die Hauptachsen symmetrische, geschlossene Kurve von länglicher Form und besitzt vier reelle Scheitel. Ihre Gleichung ist x²/a² + y²/b² = 1, wobei a die große, b die kleine Hauptachse, a > b. Die Exzentrizität ist

Die Ellipse (Fig. 1) kann als affine Umbildung des Kreises über der großen Achse als Durchmesser angesehen werden. Einfachste Konstruktion der Ellipse durch Verkleinerung der Ordinaten dieses Kreises im Verhältnis P Q : R Q = b : a. Die Brennpunkte F und F' liegen innerhalb der Kurve. Die Summe der Leitstrahlen P F + P F' eines Ellipsenpunkts ist konstant gleich der großen Hauptachse 2 a. Bewegen sich zwei Punkte einer Geraden je auf den Schenkeln eines Winkels, so beschreibt jeder andre Punkt der Geraden eine Ellipse; der Ellipsenzirkel (s.d.) beruht hierauf. Polargleichung in bezug auf den Mittelpunkt:

in bezug auf den Brennpunkt

Dabei ist b²/a = p[422] der Halbparameter. Der Krümmungshalbmesser im Punkt (ξ, η) ist

in den Endpunkten der großen Achse b²/a; in denen der kleinen a²/b. Die Evolute (a x)^3/2 + (b y)^3/2 = (a² – b²)^3/2 hat vier Spitzen. Der Flächeninhalt der Ellipse ist a b π. Ihre Fußpunktkurve mit dem Mittelpunkt als Pol (x² + y²)² = a² x² + b² y².

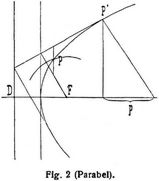
Die Parabel ist eine ins Unendliche verlängerte Ellipse; sie berührt die unendlich ferne Gerade (Fig. 2). Sie ist symmetrisch in bezug auf die durch den unendlich fernen Punkt gehende Achse. Der Endpunkt derselben heißt Scheitel; die Tangente in demselben Scheiteltangente. Da der Mittelpunkt unendlich fern ist, sind alle Durchmesser zur Achse parallel. Die Scheitelgleichung der Parabel ist y² = 2 p x. Die Subtangente ist gleich der doppelten Abszisse, die Subnormale konstant gleich dem Halbparameter p. Die Parabel besitzt nur einen reellen Brennpunkt F (0, p/2) mit der Directrix x + p/2 = 0. Alle ihre Punkte haben von Brennpunkt F und Directrix D denselben Abstand; hierauf beruht ihre punktweise Konstruktion: man zieht in beliebigem Abstand von der Directrix eine Parallele zu letzterer und beschreibt mit demselben Abstand von F aus einen Kreisbogen; der Schnittpunkt beider liefert sodann einen Punkt P der Parabel. Die Scheiteltangente ist Ort der Fußpunkte der vom Brennpunkt auf die Tangenten gefällten Lote, die Directrix Ort der Spitze eines rechten Winkels, dessen beide Schenkel die Parabel berühren. Zieht man daher einen beliebigen Strahl durch F bis zu der durch den Scheitel gehenden Ordinatenachse, so berührt die im Schnittpunkt auf demselben errichtete Senkrechte die Parabel im Punkte P'. Läßt man also einen rechten Winkel an der Ordinatenachse so gleiten, daß der eine Schenkel immer durch den Brennpunkt geht, so bildet der andre Schenkel stets eine Parabeltangente, woraus sich eine einfache Konstruktion der Kurve ergibt. Der Umkreis eines beliebigen der Parabel umbeschriebenen Dreiecks geht durch den Brennpunkt. Die Polargleichung in bezug auf den Brennpunkt als Pol ist r (1 + cos φ) = p. Krümmungsradius im Punkt (ξ, η) ist

im Scheitel hat er den Wert p. Die Evolute ist eine Neilsche Parabel: 27 p y² = 8 (x – p)³. Der Flächeninhalt der Parabel bis zum Punkt (ξ, η) ist ¹/₃ ξ η; die Länge des Parabelbogens

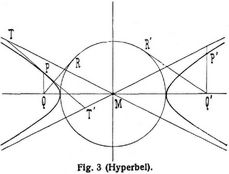
Die Hyperbel besitzt in ihren beiden unendlich fernen Punkten Tangenten, welche sich im Mittelpunkt schneiden und Asymptoten heißen (Fig. 3). Die Kurve besteht scheinbar aus zwei Teilen, welche jedoch im Unendlichen zusammenhängen. Sie besitzt eine große Halbachse, auf welcher die reellen Scheitel liegen, und eine kleine, welche die Kurve in imaginären Punkten trifft. Die Hyperbel ist in bezug auf beide symmetrisch. Ihre Gleichung ist x²/a² – y²/b² = 1. Die Brennpunkte liegen auf der großen Achse auf der konkaven Seite der einzelnen Zweige. Die Exzentrizität ist

Die Differenz der Leitstrahlen ist für alle Hyperbelpunkte konstant gleich der großen Achse (Entfernung der reellen Scheitel). Konstruktion der Hyperbel: Beschreibe über der großen Achse als Durchmesser einen Kreis; ziehe an ihn vom Endpunkt Q einer Abszisse eine Tangente Q R und verkleinere sie im Verhältnis b : a, so erhält man die Ordinate P Q der Hyperbel. Die Abschnitte einer Sekante zwischen Kurve und Asymptote sind einander gleich, daher halbiert der Berührungspunkt P das zwischen die Asymptoten fallende Stück T T' der Tangente. Der Inhalt des Dreiecks T T' M, welches eine Tangente mit den Asymptoten bildet, ist konstant. Auf die Asymptoten als Koordinatenachsen bezogen, lautet die Gleichung der Hyperbel x y = c², Polargleichung in bezug auf den Mittelpunkt

in bezug auf einen Brennpunkt als Pol

Krümmungsradius im Punkt (ξ, η):

in den Endpunkten der großen Achse b²/a. Die Evolute ist

Die Hyperbel heißt gleichseitig mit a = b, also [423] x² – y² = a²; bei einer solchen stehen die Asymptoten aufeinander senkrecht, und konjugierte Durchmesser haben gleiche Länge. Ihre Fußpunktkurve ist eine Lemniskate.

Kegelschnitte, kubische, s. Raumkurven. Vg. a. Kurvenabsteckung.

Literatur: [1] Salmon, G., Analytische Geometrie der Kegelschnitte, deutsch von Fiedler, 6. Aufl., Leipzig 1903. – [2] Gundelfinger, S., Vorlesungen aus der analytischen Geometrie der Kegelschnitte, herausg. von Dingeldey, Leipzig 1895. – [3] Hesse, O., Sieben Vorlesungen aus der analytischen Geometrie der Kegelschnitte, Leipzig 1874. – [4] Clebsch, A., Vorlesungen über Geometrie, herausg. von Lindemann, Abt. 2, Bd. 1, Leipzig 1876. – [5] Steiner, J., Vorlesungen über synthetische Geometrie, 1. Teil, Die Theorie der Kegelschnitte in elementarer Darstellung, bearbeitet von Geifer; 2. Teil, Die Theorie der Kegelschnitte, gestützt auf projektivische Eigenschaften, bearbeitet von Schröter, 3. Aufl., Leipzig 1898. – [6] Seeger, H., Die Fundamentaltheorien der neueren Geometrie und die Elemente der Lehre von den Kegelschnitten, Braunschweig 1880. – [7] Zeuthen, H.G., Grundriß einer elementar-geometrischen Kegelschnittslehre, Leipzig 1882. – [8] Erler, W., Die Elemente der Kegelschnitte in synthetischer Behandlung, 6. Aufl., Leipzig 1903. – [9] Lange, Synthetische Geometrie der Kegelschnitte, 2. Aufl., Berlin 1900. – [10] Schlotke, Die Kegelschnitte und ihre wichtigsten Eigenschaften, Dresden 1903. – [11] Thomae, Die Kegelschnitte in rein projektiver Behandlung, Halle 1894.

Wölffing.

Fig. 1.

Fig. 2.

Fig. 3.