Kurvenabsteckung

Kurvenabsteckung. Für technische Anlagen handelt es sich meistens um die Absteckung freier Kurven, von Kegelschnitten (namentlich Ellipsen und Parabeln) und von Kreisbogen im Anschluß an im Felde gegebene oder nach dem vorliegenden Plan ins Feld zu übertragende gerade Linien.

Die freien, mit dem Kurvenlineal oder aus freier Hand zu zeichnenden Kurven lassen sich den zu verfolgenden Geländelinien am besten anpassen und genügen für viele Anlagen vollständig. Die zu ihrer Absteckung erforderlichen Stücke werden maßstäblich aus dem Plan entnommen und danach ins Feld übertragen.

Die Kegelschnitte eignen sich sehr gut als Kurven beim Wege- und Wasserbau, da in ihnen ein allmählicher Uebergang von den stärkeren Krümmungen zu den schwächeren Krümmungen und zu anschließenden geraden Strecken stattfindet, sie ferner bei geeigneter Wahl des Verfahrens sehr leicht den örtlichen Verhältnissen angepaßt und mit den einfachsten Hilfsmitteln ohne vorherige Rechnungen abgesteckt werden können. Auch sind die Kegelschnitte als Ersatz für die Kreisbogen mit Uebergangskurven beim Eisenbahnbau verwendet worden.

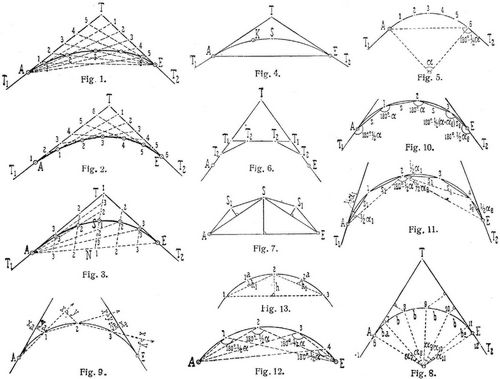
Ellipsen und Parabeln können in einfacher Weise abgesteckt werden, indem auf den Tangenten T₁ und T₂ vom Tangentenschnittpunkt T aus n auf jeder der beiden Tangenten unter sich gleiche, im übrigen aber beliebig lange Stücke abgesteckt und die Schnittpunkte der in Fig. 1 und 2 dargestellten Verbindungslinien der Teilpunkte 1, 2, ... n bestimmt werden, oder indem noch die Linien A E und N T in 2 n gleiche Stücke eingeteilt und die Schnittpunkte der[19] in Fig. 3 dargestellten Linien bestimmt werden [1]. Wenn bei letzterer Konstruktion die auf N S oder die auf S T liegenden Teilpunkte nicht gut benutzt werden können, kann auch der Kurvenzweig S E mit den auf S T liegenden Teilpunkten oder der Kurvenzweig A S auch mit den auf N S liegenden Teilpunkten abgesteckt werden.

Die sich nach Fig. 1 ergebende Kurve ist eine Ellipse oder, wenn A T E ein gleichseitiges Dreieck bilden, ein Kreis, während die sich nach Fig. 2 und 3 ergebenden Kurven Parabeln sind. Unter im übrigen gleichen Verhältnissen hat die sich nach Fig. 1 ergebende Kurve die kleinste und die sich nach Fig. 2 ergebende Kurve die größte Scheitelhöhe. Weniger einfach ist die Absteckung der Kegelschnitte nach dem für die Kreiskurven üblichen Verfahren [2].

Uebersicht der wichtigsten in Deutschland gebräuchlichen Kurventafeln:

[20] Bei der Absteckung der Kreiskurven sind in der Regel zuerst die Hauptlinien und Hauptpunkte der Kreiskurven und dann die Kleinpunkte der Kurve abzustecken. Die Hauptlinien der Kreiskurven sind (Fig. 4): 1. Die Tangenten T₁ und T₂ im Anfangspunkte A und im Endpunkte E der Kurve und 2. die Sehne A E, während die Hauptpunkte der Kreiskurven 3. der Anfangspunkt A und der Endpunkt E der Kurve, 4. der Tangentenschnittpunkt T der beiden Tangenten T₁ und T₂, 5. der Scheitelpunkt S der Kurve und die Kleinpunkte der Kreiskurven, 6. die einzelnen Punkte der Kurve selbst sind. In dem vorliegenden Plane oder im Felde werden in der Regel als Stücke für die Bestimmung der Kreiskurve vorkommen: 1. die Tangenten T₁ und T₂, 2. der Radius r, 3. der Anfangspunkt A und der Endpunkt E, 4. irgend ein andrer Punkt K der Kreiskurve. Wenn drei dieser Bestimmungsstücke gegeben sind, so ist die Kurve bestimmt. Die gegenseitige Lage der im Felde gegebenen Stücke wird durch Messung bestimmt, wonach die abzudeckenden und die zur Probe für die Richtigkeit aller Operationen nachzumessenden Stücke nach einfachen Formeln der Trigonometrie und der analytischen Geometrie berechnet [3] oder aus geeigneten Tabellen entnommen werden [7]. Hiernach wird die Absteckung der Hauptlinien und Hauptpunkte sowie die Probenachmessung ausgeführt. Unter besonderen Umständen kann die zu lösende Absteckungsaufgabe auch die sein, daß nach einer oder zwei bereits im Felde abgesteckten Kreiskurven einzelne Hauptpunkte und Hauptlinien zu bestimmen sind, z.B. die an den Endpunkt einer Kurve anschließende Tangente durch Absetzen des Winkels γ = 180° – ¹/₂α (Fig. 5) oder die Richtung und der Berührungspunkt B einer durch einen gegebenen Punkt P gehenden Tangente oder die Richtung und die Berührungspunkte B₁ und B₂ einer Tangente für zwei Kreiskurven ([7], Knoll). Verwandt hiermit ist die Absteckung der Hauptlinien und Hauptpunkte der aus mehreren sich berührenden Kreisbogen zusammengesetzten Korbbogen ([7], Knoll). Falls die in der Regel von den Tangenten T₁ und T₂ oder von der Sehne A E aus abzudeckenden Kleinpunkte der Kurve von diesen Linien aus nicht genügend genau abgesteckt werden können, weil die abzusetzenden rechtwinkligen Abstände zu lang sind, so sind im Anschluß an die Absteckung der Hauptlinien und Hauptpunkte noch Hilfstangenten T₁ T₁, T₂ T₂ ... (Fig. 6) oder Hilfssehnen A S, A S₁ und S S₁ ... (Fig. 7) abzustecken, von denen die Absteckung der Kleinpunkte mit genügender Genauigkeit erfolgen kann. Die Absteckung der Kleinpunkte erfolgt nach vielen verschiedenen Verfahren je nach den Anforderungen, die im einzelnen Falle gestellt werden, und je nach den Instrumenten, die für die Absteckung zur Verfügung stehen. – Das am meisten gebräuchliche Verfahren ist die Absetzung gleicher Abszissenunterschiede von 2, 5, 10, 20 ... m und der zugehörigen rechtwinkligen Ordinaten auf den Tangenten oder den Sehnen. Mit dem Radius r der Kurve ergeben sich die Ordinaten y, welche von der Tangente aus bei den vom Berührungspunkte der Kurve abzurechnenden Abszissen x abzusetzen sind, nach

und die Ordinaten y, welche von der Sehne aus bei den von der Mitte der Sehne ab zu rechnenden Abszissen x abzusetzen sind, bei einem Zentriwinkel α des zur Sehne s gehörigen Kurvenstücks nach h = 2 r sin^{2 1}/₄ α und y = h – y. Wird verlangt, daß die abgesteckten Kurvenpunkte gleichen Abstand voneinander haben oder daß direkt bestimmte Kurvenpunkte, wie z.B. die Stationspunkte der Trace, abzustecken sind, so werden die zu den bekannten Bogenlängen b_n gehörigen Zentriwinkel α_n berechnet (Fig. 8) und nach x_n = r sin α_n, y_n = 2 r sin^{2 1}/₂ α_n die auf den Tangenten von den Berührungspunkten der Kurve aus abzusetzenden Abszissen und Ordinaten erhalten. Beide Methoden der Kleinpunktabsteckung werden als Koordinatenmethode bezeichnet. – In solchen Fällen, wo die Kleinpunkte nicht gut von den Haupttangenten und Hauptsehnen aus abgesteckt werden können, können sie von den verlängerten Sehnen oder Tangenten der Kleinpunkte (Einrückungsmethode) oder nach den Sehnen der Kleinpunkte und den zugehörigen Sehnenwinkeln (Sehnenverfahren) abgesteckt werden. Der Punkt 1 (Fig. 9) wird von der Haupttangente durch Absetzen von x_a und y_a bestimmt, darauf die Sehne A₁ verlängert, worauf Punkt 2 durch Absetzen von x und y erhalten wird u.s.w. Aehnlich, aber weniger zweckmäßig ist die Absteckung von der verlängerten Tangente. Die Absteckung nach den Sehnen und Sehnenwinkeln ist in Fig. 10, worin mit α und α_e die zu den Sehnen s und s_e gehörigen und nach sin ¹/₂ α = s : 2 r folgenden Zentriwinkel bezeichnet sind. Im freien, übersichtlichen Gelände können die Kleinpunkte nach den Peripheriewinkeln ¹/₂ α₁ und den zugehörigen Sehnen s₁ abgesteckt werden, indem auf dem Anfangspunkte A der Kurve (Fig. 11) von der Haupttangente T₁ aus der 1-, 2-, 3- ... fache Peripheriewinkel abgesteckt und zwischen den damit bestimmten Richtungen die Sehnen s₁ abgesetzt werden. Kann die Kurve in dieser Weise nicht ganz vom Anfangspunkte A aus abgesteckt werden, so kann die Absteckung von irgend einem Kurvenpunkte aus (Fig. 11, Punkt 2) fortgesetzt werden. Zur einfachen Absetzung der 1-, 2-, 3- ... fachen Peripheriewinkel kann ein an jedem Theodoliten anzubringender Apparat (Curve-ranger) benutzt werden [4], Ferner können die durch die 1-, 2-, 3- ... fachen Peripheriewinkel bestimmten Richtungen auch durch Einmessung ihrer Schnittpunkte mit der Tangente T₂ bestimmt werden ([7], Becker). – Ebenfalls im freien, übersichtlichen Gelände können Kleinpunkte bestimmt werden, indem solche Punkte aufgesucht werden, auf denen die Richtungen nach dem Anfangspunkte und Endpunkte der Kurve den Peripheriewinkel 180°–¹/₂ α miteinander einschließen (Fig. 12). Hiernach kann mit den gewöhnlichen zum Abstecken von rechten Winkeln dienenden Winkelspiegeln oder Prismen der die beiden Punkte A und E verbindende Halbkreis und mit einem Winkelspiegel, dessen Spiegel verstellbar sind (Arcograph [5]), oder mit einem Doppelprisma, mit einem festen und einem verstellbaren Prisma (Dechersche Prismentrommel [6]), ebenso wie mit passend eingerichteten Spiegelsextanten oder Prismenkreisen jeder beliebige Kreisbogen abgesteckt werden. Diese Instrumente können auch beim Kurvenabstecken überall da sehr nützlich sein, wo dieselben Winkel vielfach abzustecken oder nachzumessen[21] sind. – Die Pfeilhöhe eines Kreisbogens ist h = 2 r sin^{2 1}/₂ α und die Pfeilhöhe der Hälfte dieses Kreisbogens h₁=2 r sin^{2 1}/₄ α, demnach

oder wenn ¹/₂ α ein kleiner Winkel ist, genähert

also h₁ = ¹/₄ h. Hierauf beruht die Viertelsmethode, wonach in bereits abgesteckte Kurven weitere Kurvenpunkte eingeschaltet oder auch ganze Kurven abgesteckt werden können. Sind die Kurvenpunkte 1, 2, 3... (Fig. 13) im Felde abgedeckt, so wird h gemessen und auf der Mitte der Sehnen 12, 23 ... die Pfeilhöhe h₁ = ¹/₄ h abgesetzt, wodurch die Kurvenpunkte 1a, 2a ... erhalten werden, wonach zwischen 1 und 1 a, 1a und 2, 2 und 2a ... weitere Punkte durch Absetzen der Pfeilhöhen h₂ = ¹/₄ h₁ erhalten werden u.s.w. In gleicher Weise kann zwischen zwei Punkten A und E ein Kreisbogen abgedeckt werden, wenn die Pfeilhöhe h gegeben oder aus der Sehne A E = s und dem Radius r nach sin ¹/₂ = s : 2 r und h = 2 r sin^{2 1}/₄ α berechnet wird. Genügt an Stelle des Kreisbogens eine Parabel, so ist h = s² : 8 r. Die Berechnung der zur Abdeckung der Hauptlinien und Hauptpunkte sowie der Kleinpunkte erforderlichen Stücke wird vielfach wesentlich erleichtert oder ganz unnötig bei Benutzung zweckmäßig eingerichteter Kurventabellen, welche in großer Zahl vorliegen [7].

Literatur: [1] Kaven, A. v., Vorträge über Ingenieurwissenschaften, Abt. 1, Hannover 1870. – [2] Hecht (s. [7]) und Bauernfeind, Elemente der Vermessungskunde, 7. Aufl., Stuttgart 1890. – [3] Veltmann und Koll, Formeln der niederen und höheren Mathematik sowie für die Teilung der Grundstücke und für Tracierungsarbeiten, 3. Aufl., Bonn 1899. – [4] Usill, Practical surveying, 4. Aufl., London 1896. – [5] Pockels, Der Arkograph, Deutsche Bauztg. 1875, Nr. 5. – [6] Decher, Die Prismentrommel, München 1888. – [7] Sarrazin und Oberbeck, Taschenbuch zum Abdecken von Kreisbögen, 17. Aufl., Berlin 1907; Knoll, Taschenbuch zum Abdecken der Kurven an Straßen und Eisenbahnen, 2. Aufl., neu bearbeitet von Weitbrecht, Stuttgart 1902; Hecht, Kurventafeln zum Tracieren von Eisenbahnen, Chausseen u.s.w., Braunschweig 1871; Ders., Hilfsbuch zum Abdecken von Kreisbögen, Dresden 1893; Ders., Hand- und Hilfsbuch zum Abdecken von Eisenbahn- und Straßenkurven, Dresden 1893; Jordan, Kreiskoordinaten für 200 Radien, Leipzig 1881; Kröhnke, Handbuch zum Abdecken von Kurven, 14. Aufl., Leipzig 1902; Hanhart u. Waldner, Tracierungshandbuch, 2. Aufl., Berlin 1904; Winkel, Handbuch zum Abdecken von Kurven, Berlin 1873; Morawitz, Die Straßen- und Eisenbahnkurven, 4. Aufl., Wien, Pest, Leipzig 1875; Becker, Die Abdeckung von Straßen- und Eisenbahnkurven, 2. Ausgabe, Wien 1891; Gysin, Peripheriewinkeltafeln, Liestal 1885; Elb, Taschenbuch zum Abdecken von Kreisbögen, Wilhelmshaven 1879.

Otto Koll.

Fig. 1., Fig. 2., Fig. 3., Fig. 4., Fig. 5., Fig. 6., Fig. 7., Fig. 8., Fig. 9., Fig. 10., Fig. 11., Fig. 12., Fig. 13.