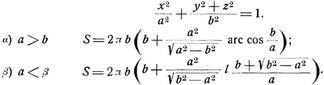- Komplanation
Komplanation, die Berechnung des Inhalts krummer Flächen.
I. Komplanation in Parallelkoordinaten. Gesucht Stück S der Fläche z = f(x, y), das begrenzt ist durch die Ebenen x = x0 und x = x1 und die Zylinderflächen y = φ (x) und y = φ (x). Es ist
Beispiel: Böhmisches Gewölbe, d.h. Fläche der Kugel x2 + y2 + z2 = c2, begrenzt durch die Ebenen x = 0, x = a; y = 0, y = b. Es ist: S = c(aα + bβ – cγ), wenn
Besondere Fälle der Komplanation in Parallelkoordinaten.
a) Bei einer Drehungsfläche, die durch Drehung der Kurve y = f (x) um die x-Achse entsteht, hat das von den Ebenen x = x0 und x = x1 begrenzte Stück die Fläche
Beispiele: Drehungsellipsoid
b) Der Körper sei begrenzt durch zwei Zylinderflächen y = φ (x) und z = ψ (x), durch die Ebenen y = 0, z = 0, x = x0, x = x1; so ist die Fläche des ersten Zylinders, die an der Begrenzung teilnimmt,
die entsprechende Fläche des zweiten Zylinders
Beispiele:
α) Parabolisches Klostergewölbe gibt mit
β) Elliptisches Klostergewölbe
das gedrückte Gewölbe.
das überhöhte Gewölbe. γ) Kreisförmiges Klostergewölbe
II. Komplanation im gemischten Polarsystem. Das auf der Fläche z = f(r, φ) durch die Zylinderfläche r = f1 (φ) und die Ebenen φ = φ0 und φ = φ1 begrenzte Stück hat die Fläche
III. Komplanation im reinen Polarsystem Das auf der Fläche r = f(φ, ϑ) durch die Kegelfläche (ϑ)f = fx(d) und die Ebenen ϑ = ϑ0 und ϑ = ϑ1 begrenzte Stück ist
Literatur: [1] Serret, Lehrbuch der Differential- und Integralrechnung, deutsch von Harnack, Bd. 2, 2. Hälfte, Leipzig 1885, 5. Kap. – [2] Schlömilch, O., Uebungsbuch zum Studium der höheren Analysis, 2. Teil, 2. Aufl., Leipzig 1874, 17–18; 27–29.
Wölffing.
http://www.zeno.org/Lueger-1904.