Polytropische Zustandsänderungen

Polytropische Zustandsänderungen, Ausdruck der Wärmetheorie, eingeführt von Zeuner [1]. Wirkt auf die Oberfläche eines Körpers ein gleichmäßig verteilter Normaldruck von p pro Flächeneinheit und es ändert sich p mit dem Körpervolumen v derart, daß

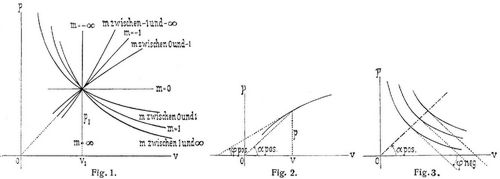
unter m und C irgendwelche Konstante verbanden, so hat man eine polytropische Zustandsänderung des betreffenden Körpers. Meist wird in 1. v auf die Gewichtseinheit bezogen (spezifisches Volumen). Werden die p als Ordinaten bei den zugehörigen v als Abszissen aufgetragen, so entsteht eine polytropische Kurve. In Fig. 1 sind einige durch den Punkt p₁, v₁ gehende Kurven dieser Art angedeutet. Die polytropischen Zustandsänderungen spielen in der technischen Thermodynamik eine hervorragende Rolle, da die wichtigsten Zustandsänderungen von Gasen und Dämpfen genau oder annähernd unter die Form 1. fallen und selbst ganze Indikatordiagramme mit genügender Genauigkeit[189] durch eine Anzahl polytropischer Kurven dargestellt werden können, worauf z.B. eine kalorimetrische Beurteilung von Luft- und Gasmaschinen beruht [3], [12], I, S. 199, 294.

Aus 1. folgen:

Bezeichnet an irgend einer Stelle p, v einer polytropischen Kurve f deren Neigungswinkel gegen die v-Achse, so hat man den Exponenten in 1.:

(Fig. 2), wonach alle polytropischen Kurven von gleichem m aber verschiedenen C jede vom Koordinatenursprung ausgehende Gerade unter gleichen Winkeln φ schneiden (Fig. 3). Für einen Uebergang von p₁ v₁ in p, v läßt sich der zu seiner Darstellung durch eine polytropische Kurve anzunehmende Exponent m nach 1. erhalten:

Als p₁ v₁ und p, v kann man den Anfangspunkt und Endpunkt eines Uebergangs wählen oder irgendwelche andre Punkte desselben, bei welchen man besonderes Gewicht auf möglichsten Anschluß an die wirkliche Druckkurve legt. Ueber graphische Bestimmung polytropischer Kurven von gegebenen m, p₁ v₁ s. [4], [6] – [9], über die Arbeit zur Ueberwindung des Druckes p s. Aeußere Arbeit, Bd. 1, S. 103.

Für Gase, welche dem Boyle-Gay-Lussacschen Gesetze (s.d.)

pv = R T

5.

folgen, stellt 1. die Bedingung für das Konstantbleiben der spezifischen Wärme (s.d.) dar, d.h. des Verhältnisses der Wärmezufuhr d Q pro Gewichtseinheit zur Temperaturänderung d T, für welches dann gilt:

d Q/d T = c = m – k/m – 1 c_v, Q = c (T –T₁),

6.

wenn c_p, c_v die spezifischen Wärmen bei konstantem Drucke und konstantem Volumen, und k = c_p : c_v, für atmosphärische Luft c_p = 0,23751, c_v = 0,16844, k = 1,41. Ueber die Temperatur, äußere Arbeit und Aenderung der inneren Arbeit für polytropische Zustandsänderungen von Gasen s. Gase, Bd. 4, S. 277. Anwendung polytropischer Zustandsänderungen beim Ausfluß von Gasen und Dämpfen aus Gefäßmündungen s. Bd. 4, S. 283, und [12], I, S. 305, 362.

Literatur: [1] Zeuner, Grundzüge der mechanischen Wärmetheorie, Leipzig 1866, S. 143 (ausführlicher Technische Thermodynamik, I, Leipzig 1900, S. 147, 239). – [2] Grashof, Theoretische Maschinenlehre, I, Leipzig 1874, S. 112, 208, 559. – [3] Weyrauch, Zur Beurteilung von Luft- und Gasmaschinen, Zeitschr. d. Ver. deutsch. Ing. 1880, S. 185 (Zahlenkorrektur 1881, S. 226). – [4] Brauer, Konstruktion gesetzmäßiger Expansionskurven von der allgemeinen Form pv^m = C, Zeitschr. wie [2], 1885, S. 433. – [5] Tobell, Ueber die graphische Untersuchung und Vorausbestimmung von Indikatordiagrammen an Dampfmaschinen, Techn. Blätter 1889, S. 22. – [6] Pröll, Ueber Indikatordiagramme und graphische Beziehungen zwischen Druck, Volumen und Temperatur, Zeitschr. wie [2], 1891, S. 988, 1022. – [7] Tolle, Neue Konstruktion der polytropischen Kurve, Zeitschr. wie [2], 1894, S. 1456. – [8] Hartmann, Gleichzeitige Bestimmung der Polytrope und Charakteristik für ein angenommenes Indikatordiagramm, Zeitschr. wie [2], 1895, S. 194. – [9] Wagner, Verfahren zur Aufzeichnung der polytropischen Kurve, Zeitschr. wie [2], 1896, S. 707. – [10] Lorenz, Technische Wärmelehre, München und Berlin 1904, S. 47, 173. – [11] Fischer, Viktor, Die Verwendung eines logarithmisch geteilten Koordinatensystems in der Wärmemechanik, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1907, S. 294. – [12] Weyrauch, Grundriß der Wärmetheorie, I, Stuttgart 1905, S. 54, 158, 163, 198, 271, 284; II, Stuttgart 1907, S. 45, 129, 305, 362. – [13] Dingeldey, Zeitschr. f. Math. und Physik 1907, S. 87.

Weyrauch.

Fig. 1., Fig. 2., Fig. 3.