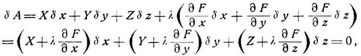Prinzip der virtuellen Geschwindigkeiten

Prinzip der virtuellen Geschwindigkeiten oder der virtuellen Verschiebungen ist eine allgemeine Form des Ausdrucks des Gleichgewichts eines Kräftesystems, welches an einem Massenpunktsystem angreift. Es wird dabei vorausgesetzt, daß das System der Angriffspunkte im allgemeinen Fall nicht frei beweglich, sondern an Bedingungen geknüpft ist, die entweder durch Gleichungen zwischen den Koordinaten der Angriffspunkte selbst oder durch solche zwischen diesen Koordinaten und ihren unendlich kleinen Veränderungen gegeben sind (holonome und nichtholonome Bedingungen bezw. Systeme). Veränderungen des Systems, bei denen den genannten Bedingungen nicht widersprochen wird, heißen virtuelle Verschiebungen. Das Prinzip sagt nun aus, daß im Falle des Gleichgewichts die (algebraische) Summe der Arbeiten der wirkenden Kräfte bei jeder unendlich kleinen virtuellen Verschiebung des Systems aus der Gleichgewichtslage verschwindet (bezw. unendlich klein höherer Ordnung wird). In dieser allgemeinen Form läßt sich das Prinzip nicht streng beweisen, da über die Realisierung der vorausgesetzten Bedingungen nichts ausgesagt wird; es stellt vielmehr die Zusammenfassung und natürliche Erweiterung einer großen Zahl beweisbarer Einzelfälle dar.

Analytische Formulierung des Prinzips. Sind x_i y_i z_i die Koordinaten des Angriffspunktes der Kraft P_i mit den Komponenten X_i Y_i Z_i und δ x_i δ y_i δ z_i die Veränderungen dieser Koordinaten bei einer virtuellen Verschiebung, so ist die Arbeit δ A der wirkenden Kräfte: δ A = Σ (X_i δ x_i + Y_i δ y_i + Z_i δ z_i), wobei sich die Summe auf die sämtlichen n Angriffspunkte von Kräften erstreckt. Dabei bestehen entweder holonome Bedingungsgleichungen wie F_k (x_i y_i, z_i, ... x_i y_i z_i ... x_n y_n z_n) = 0, aus denen für die Verschiebungen

folgt, oder nichtholonome Bedingungsgleichungen von der Art wie Σ (φ_i δ x_i + ψ_i δ y_i + χ_i δ z_i) = 0, wobei die φ_i ψ_i χ_i von den Koordinaten der Angriffspunkte abhängen. Eliminiert man nun mit Hilfe der r Bedingungsgleichungen so viele von den δ x_i δ y_i ..., als solche Gleichungen vorhanden sind, so wird die virtuelle Arbeit δ A nur mehr durch 3 n – r unabhängige Veränderungen δ x_i ... ausgedrückt. Da δ A bei beliebiger Wahl derselben nach dem genannten Prinzip verschwinden muß, so müssen die Faktoren dieser δ x_i ... einzeln verschwinden, und man erhält durch Nullsetzen derselben 3 n – r Gleichgewichtsbedingungen, die mit den r Bedingungen zusammen, falls diese holonom sind, bei gegebenen Kräften die Gleichgewichtslagen bestimmen. Nichtholonome Systeme haben bei gegebenen Kräften noch unendlich viele Gleichgewichtslagen.

Ansatz von Lagrange. Anstatt die Elimination der δ x_i ... mittels der Bedingungsgleichungen vorzunehmen, kann man auch nach dem Vorgange von Lagrange den Ausdruck für die virtuelle Arbeit δ A durch Hinzufügung der mit noch zu bestimmenden Multiplikatoren λ_k versehenen linken Seiten der differenzierten holonomen bezw. der nichtholonomen Bedingungsgleichungen erweitern. Auch dieser erweiterte Ausdruck der Arbeit verschwindet bei den[240] virtuellen Verschiebungen, da ja die mit den Multiplikatoren λ_k versehenen Ausdrücke dabei Null sind. Die Gleichgewichtsbedingungen werden nun dadurch erhalten, daß man die Faktoren sämtlicher 3 n δ x_i ... einzeln gleich Null setzt und den dabei außer acht gelassenen Bedingungsgleichungen hinterher dadurch Rechnung trägt, daß man die unbestimmt eingeführten Multiplikatoren so bestimmt, daß den holonomen Bedingungsgleichungen Genüge geschieht. Bei nur holonomen Bedingungsgleichungen erhält man so 3 n + r Gleichgewichtsbedingungen, aus welchen sich die 3 n Koordinaten der Gleichgewichtslage und die r eingeführten Multiplikatoren λ_k berechnen lassen. Die mit den λ_k versehenen Summanden der Gleichgewichtsbedingungen haben die Bedeutung von Kräften (Reaktionskräften, Verbindungskräften), welche die Aufrechterhaltung der Bedingungsgleichungen bewirken.

Beispiele: 1. Die Gleichgewichtsbedingungen am freien starren Körper. Bei einer Parallelverschiebung δ x längs der X-Achse ist die Arbeit der Kräfte δ x Σ X_i, sie verschwindet, wenn Σ X_i = 0 ist; ähnlich ergibt sich Σ Y_i = 0, Σ Z_i = 0. Bei Drehung des Körpers um die Z-Achse um den Winkel δ α wird die Arbeit: δ α Σ (x_i Y_i – X_i y_i), woraus folgt: Σ (x_i Y_i – X_i y_i) = 0 und ähnlich Σ (y_i Z_i – Y_i z_i) = 0 und Σ (z_i X_i – Z_i x_i) = 0.

2. Gleichgewicht auf einer glatten Fläche von der Gleichung F (x y z) = 0 (holonome Bedingungsgleichung). Es wirke eine Kraft X Y Z auf einen Punkt x y z der Fläche. Bedingungsgleichung für die Verschiebungen:

Erweiterter Ansatz nach Lagrange für die virtuelle Arbeit:

woraus die Gleichgewichtsbedingungen folgen:

die zusammen mit F = 0 aussagen, daß im Gleichgewichtsfalle die Flächennormale im Angriffspunkte mit der Richtung der Kraft übereinstimmt und daß die drei Komponenten der Reaktion denen der Kraft entgegengesetzt gleich sind.

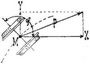
3. Ein zweiräderiger Wagen ohne rollende, aber mit sehr großer gleitender Reibung auf einer horizontalen Ebene fahrend wird in der Mitte M (x y) der Achse von einer horizontalen Kraft P mit den Komponenten X Y angegriffen. Wann ist er im Gleichgewicht? Zwischen den Koordinaten x y, dem Winkel φ der Achse des Wagens mit der X-Achse und den virtuellen Verrückungen von M besteht die nichtholonome Bedingungsgleichung: δ y + δ x ctg φ = 0. Der erweiterte Ansatz für die virtuelle Arbeit lautet:

woraus die Gleichgewichtsbedingungen folgen: X + μ = 0, Y + μ ctg φ = 0. Sie sagen, da sie x und y nicht enthalten, aus, daß der Wagen in jedem Punkt der Ebene im Gleichgewicht sein kann, nur muß die Richtung der Kraft Y : X = ctg μ mit derjenigen der Wagenachse übereinstimmen.

Für die Anwendung des Prinzips der virtuellen Geschwindigkeiten ist die Lehre von den Freiheitsgraden der Systeme von großer Bedeutung, da sie allein alle möglichen Bewegungen eines Systems anzugeben vermag. – Vgl. a. Fachwerke, Bd. 3, S. 552 ff.

Finsterwalder.