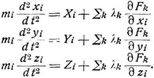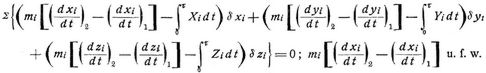Prinzip von d'Alembert

Prinzip von d'Alembert. Es dient zur Aufstellung der Bewegungsgleichungen eines materiellen Systems. Dieses bestehe aus den n Massen m_i in den Punkten mit den Koordinaten x_i y_i z_i, an welchen Kräfte P_i mit den Komponenten X_i Y_i Z_i angreifen. Zwischen den Koordinaten bestehe eine Anzahl von Bedingungsgleichungen F_k = 0, die zunächst unabhängig von der Zeit vorausgesetzt werden. Zur Zeit t haben die Massen die Beschleunigungskomponenten

Da das System Bedingungen unterliegt, so werden die Differenzen

nicht verschwinden, wie es bei einem System freier Massenpunkte nach dem Grundgesetz der Dynamik – Kraft ist gleich Masse mal Beschleunigung – der Fall ist. Diese Differenzen werden als Verbindungskräfte oder auch als [241] verlorene Kräfte bezeichnet. Das d'Alembertsche Prinzip sagt nun aus, daß diese Verbindungskräfte (verlorenen Kräfte) mit Rücksicht auf die Bedingungen des Systems zu jedem Zeitpunkt im Gleichgewicht sein müssen. Wären sie es nämlich nicht, so müßten sie in Verbindung mit den äußeren Kräften X_i Y_i Z_i den Massen m_i andre Beschleunigungen als die vorausgesetzten erteilen.

Analytische Formulierung des Prinzips. Man braucht nur auf die Verbindungskräfte (verlorenen Kräfte), die mit Rücksicht auf die Bedingungen des Systems im Gleichgewicht sein müssen, das Prinzip der virtuellen Geschwindigkeiten anzuwenden und die virtuelle Arbeit derselben gleich Null zu setzen, so erhält man

wozu noch die infolge der Bedingungsgleichungen bestehenden Beziehungen zwischen den δ x_i ... treten, z.B. für F_k = 0

Nichtholonome Bedingungsgleichungen werden unmittelbar eingeführt. Enthalten die endlichen (holonomen) Bedingungsgleichungen die Zeit t, so wird dieselbe bei der Differentiation behufs Bildung der Gleichung zwischen den δ x_i ... nicht als variabel behandelt. Sind in nichtholonomen Bedingungsgleichungen Glieder mit d t vorhanden, so bleiben sie bei Anwendung des d'Alembertschen Prinzipes weg. Erweitert man den Ausdruck der virtuellen Arbeit der Verbindungskräfte durch die mit Faktoren λ_k multiplizierten linken Seiten der differenzierten bezw. nichtholonomen Bedingungsgleichungen und setzt man die Faktoren der einzelnen δ x_i gleich Null, so ergeben sich die Lagrangeschen Bewegungsgleichungen erster Art:

Mit den endlichen und den nichtholonomen Bedingungsgleichungen bilden sie ein System von 3 u + k Gleichungen, das zur Bestimmung der 3 u-Koordinaten und der k-Multiplikationen λ_k als Funktionen der Zeit ausreicht.

Das d'Alembertsche Prinzip gilt nicht nur für kontinuierliche Kräfte, sondern auch für Momentankräfte oder Impulse. Um den analytischen Ausdruck für diesen Fall zu erhalten, denkt man sich den Ausdruck

mit dem Zeitelement d t multipliziert und innerhalb eines sehr kurzen Zeitraumes t integriert (wobei natürlich die δ x_i ... als konstant zu betrachten sind), so erhält man

sind die Differenzen der Komponenten der Bewegungsgröße nach und vor dem Zeitraum τ,

die Komponenten der Impulse während des Zeitraums τ. Dazu treten die Bedingungsgleichungen. Die mit den Verschiebungen δ x_i ... multiplizierten Klammergrößen können als Verbindungsimpulse bezeichnet werden, die sich infolgedessen nach dem d'Alembertschen Prinzip mit Rücksicht auf die Verbindungen das Gleichgewicht halten.

Literatur: d'Alembert, J., Traité de dynamique, Paris 1743; Lagrange, Mécanique analytique, 1. Aufl. 1788,2. Aufl. 1811; Jacobi, Vorlesungen über Dynamik, Berlin 1866; Ders., Werke, Supplement, band, Berlin 1884; Voß, A., Math. Annalen 1884, Bd. 25, S. 258.

Finsterwalder.