- Schubspannungen
Schubspannungen. Allgemeines über dieselben s. Druck, Spannungen, Elastizitätslehre (allgemeine), Schubelastizität, Schubfestigkeit. Hauptschubspannungen, Spannungstrajektorien. Besondere Fälle: Nietverbindungen für Eisenkonstruktionen, Biegung, Biegungselastizität, Balken (einfache, Tabelle), Blechträger, Einsenkung, elastische Linie, Elastizitätsmodul u.s.w. und die dortige Literatur.
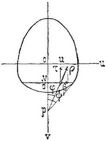
Am häufigsten hat man die Schubspannungen in den Elementen eines Stabquerschnitts unter der Voraussetzung zu bestimmen, daß der Querschnitt eine Symmetrieachse besitzt, in welcher die Schubkraft P wirkt, während auf die Mantelfläche und senkrecht zu P keine Kräfte wirken. Wir wählen für diesen Fall in der Querschnittsebene als Koordinatenachsen v, u die Symmetrieachse und eine beliebige dazu senkrechte Achse (vgl. die Figur).[823] Der Symmetrie halber werden symmetrisch zur v-Achse bei gleichem v gleiche Schubspannungen ρ auftreten, deren Vertikalkomponenten und Horizontalkomponenten durch τ, β bezeichnet sein mögen. Aus den Gleichgewichtsbedingungen folgt für ein Flächenelement an beliebiger Stelle u, v:
unter b die Querschnittsbreite bei v, unter φ den Winkel einer Geraden vom Flächenelement nach demjenigen Punkte p verstanden, in welchem die Tangente an den Querschnittsumfang bei v die v-Achse schneidet. ψ ist der Wert von φ für u = b/2. Nach 1. hat man für u = 0 stets ρ = τ, während bei gleichem τ das größte ρ für das größte φ eintreten würde. Damit alle ρ gleich wären, müßte τ proportional cos φ sein.
Speziell unter den Voraussetzungen der technischen Biegungstheorie (auch mit Berücksichtigung des Einflusses der Schubkräfte auf die Biegung, Bd. 1, S. 797) und bei vertikaler v-Achse ist τ für alle Querschnittselemente von gleichem v gleichgroß, nämlich wenn die u-Achse durch den Schwerpunkt des Querschnitts geht und im folgenden für horizontale Stäbe P = Vx, für einfach gekrümmte Stäbe P = Tx gesetzt wird, mit den Bezeichnungen Bd. 1, S. 792, 799:
Hiernach hat man für das Rechteck von der Breite b und Höhe h und für die Ellipse von der vertikalen und horizontalen Halbachse a, c:
und nach 1., 3. die größte Schubspannung, für v = 0, in der Achsschicht:
d.h. 3/2- bezw. 4/3 mal so groß als bei gleichmäßiger Verteilung auf den Querschnitt. Speziell für Quadrat und Kreis sind in 3. 4. h = b bezw. c = a. – Die Bedingungen, auf welchen die Gleichungen 1.–4. speziell für den Fall der Biegung beruhen, sind an Stellen, wo plötzliche Aenderungen von b eintreten (
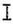 -Querschnitt, Blechträgerquerschnitt u.s.w.) nicht sämtlich gleichzeitig erfüllbar. Da nun an allen andern Stellen der betreffenden Querschnitte φ = 0, ρ = τ zu sein pflegt, so hat man in den fraglichen Fällen meist nur die Schubspannungen r in Betracht gezogen, doch muß man sich darüber klar sein, daß dies an jenen Unstetigkeitsstellen nicht zutrifft. Literatur: [1] Grashof, Theorie der Elastizität und Fertigkeit, Berlin 1878, S. 123. – [2] Ritter, Anwendungen der graphischen Statik, I, Zürich 1888, S. 61. – [3] Foeppl, Vorlesungen über technische Mechanik, III, Festigkeitslehre, Leipzig 1900, S. 59, 74, 128. – [4] Handbuch der Ingenieurwissenschaften, Bd. 2, Brückenbau, 2. Abteilung, Leipzig 1901, S. 219. – [5] Müller-Breslau, Die graphische Statik der Baukonstruktionen, I, Leipzig 1901, S. 101; (auch Neuere Methoden der Festigkeitslehre, Leipzig 1904, S. 243). – [6] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, I, Leipzig 1903, S. 366. – [7] Bach, Elastizität und Festigkeit, Berlin 1905, S. 363. – [8] Keck-Hotop, Vorträge über Elastizitätslehre, I, Hannover 1905, S. 59, 74, 128.
-Querschnitt, Blechträgerquerschnitt u.s.w.) nicht sämtlich gleichzeitig erfüllbar. Da nun an allen andern Stellen der betreffenden Querschnitte φ = 0, ρ = τ zu sein pflegt, so hat man in den fraglichen Fällen meist nur die Schubspannungen r in Betracht gezogen, doch muß man sich darüber klar sein, daß dies an jenen Unstetigkeitsstellen nicht zutrifft. Literatur: [1] Grashof, Theorie der Elastizität und Fertigkeit, Berlin 1878, S. 123. – [2] Ritter, Anwendungen der graphischen Statik, I, Zürich 1888, S. 61. – [3] Foeppl, Vorlesungen über technische Mechanik, III, Festigkeitslehre, Leipzig 1900, S. 59, 74, 128. – [4] Handbuch der Ingenieurwissenschaften, Bd. 2, Brückenbau, 2. Abteilung, Leipzig 1901, S. 219. – [5] Müller-Breslau, Die graphische Statik der Baukonstruktionen, I, Leipzig 1901, S. 101; (auch Neuere Methoden der Festigkeitslehre, Leipzig 1904, S. 243). – [6] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, I, Leipzig 1903, S. 366. – [7] Bach, Elastizität und Festigkeit, Berlin 1905, S. 363. – [8] Keck-Hotop, Vorträge über Elastizitätslehre, I, Hannover 1905, S. 59, 74, 128.Weyrauch.
http://www.zeno.org/Lueger-1904.