Trägheitsellipse

Trägheitsellipse, geometrisch abgeleitet.

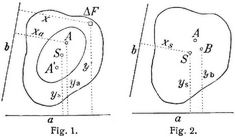
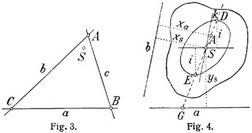
Es sei F der Flächeninhalt einer ebenen Figur, S ihr Schwerpunkt und Δ F ein unendlich kleines Element der Figur; a und b seien zwei in der Ebene gelegene Achsen und x und y ihre Abstände vom Elemente Δ F. Das Produkt Δ F · y nennt man das statische Moment des Elementes in bezug auf die Achse a. Nach der Theorie des Schwerpunktes ist das statische Moment der ganzen Fläche Σ (Δ F · y) = F · y_s. Ersetzt man nun die Flächeninhalte Δ F durch die statischen Momente Δ F · y und bestimmt deren Schwerpunkt, so findet man einen von S verschiedenen Punkt A. Mit Hilfe dieses Punktes kann der Wert Z = Σ (Δ F · y · x), das »Zentrifugalmoment« der Figur in bezug auf die Achsen a und b berechnet werden. Da A der Schwerpunkt der statischen Momente Δ F · y ist, so ist nämlich das Zentrifugalmoment gleich der Summe der statischen Momente multipliziert mit x_a oder Z = x_a Σ (Δ F · y) = F · ys · x_a. Läßt man b mit a zusammenfallen, so geht das Zentrifugalmoment in das Trägheitsmoment J für die Achse a über und es ist J = Σ (Δ F · y²) = F · y_s · y_a. Der Punkt A ist von der Lage der Achse a abhängig; zu jeder Achse a gehört ein bestimmter Punkt A. Geht die Achse a durch den Schwerpunkt S, so fällt A ins Unendliche, weil in diesem Falle y_s = 0, J dagegen von Null verschieden ist. Fällt umgekehrt die Achse a ins Unendliche, so haben alle Elemente gleiche Hebelarme; der Punkt 4 als Mittelpunkt der statischen Momente fällt daher mit dem Schwerpunkt S zusammen. Gleich wie A der Schwerpunkt der auf a bezogenen statischen Momente ist, so sei B der Schwerpunkt der auf b bezogenen statischen Momente (Fig. 2). Dann ist das Zentrifugalmoment Z auch gleich yb Σ (Δ F · x) = F · x_s · y_b. Fällt A mit b zusammen, so wird Z = 0; folglich ist auch y_b = 0, und es fällt auch B mit a zusammen (Fig. 3). Dreht sich b um A, so bewegt sich B auf a; dem Punkte A entspricht somit umgekehrt (und zwar eindeutig) die Linie a. Dem Schnittpunkte C von a und b entspricht ferner die Verbindungslinie c von A und B. Da diese Beziehungen allgemein gültig sind, so folgt, daß die Achsen und die ihnen entsprechenden Punkte ein Polarsystem bilden, dessen Mittelpunkt der Schwerpunkt S ist. Ersetzt man die Punkte A durch die symmetrisch zu ihnen gelegenen Punkte A' (Fig. 1), so besitzt das Polarsystem eine reelle Ordnungskurve, und zwar eine Ellipse, die man »Trägheitsellipse« oder »Zentralellipse« der Figur nennt. Heißt man A den »Antipol« (s.d.) von a, so ergeben sich folgende Sätze: Das Zentrifugalmoment einer Figur in bezug auf zwei Achsen ist gleich dem Flächeninhalte multipliziert mit dem Abstände des Schwerpunktes von der einen Achse und mit dem Abstand des Antipols dieser Achse von der zweiten (Z = F · y_s · x_a). Das Trägheitsmoment einer Figur in bezug auf eine Achse ist gleich dem Flächeninhalte multipliziert mit den Abständen des Schwerpunktes und des Antipols von der Achte (J = F · y_s · y_a). Sind die Achsen in bezug auf die Ellipse zueinander konjugiert, d.h. geht die eine durch den Pol der andern, so wird Z = 0. Wird die Figur durch zwei aufeinander senkrecht stehende Achsen symmetrisch geteilt, so sind diese Achsen die Ellipsenachsen.

In der Fig. 4 bilden die Punktepaare AG, DE und S ∞ eine Involution (s.d.). Folglich ist SA : SD = SE : SG. Hieraus folgt x_a – x_s : k = i : y_s oder y_s · x_a = ys · x_s + i · k. Das Zentrifugalmoment ist daher auch Z = F (ys · xs + i · k) und das Trägheitsmoment J = F (ys² + i²), da i² = (ya – ys) ys, also ys · ya = i² + ys² ist. Gehen beide Achsen durch den Schwerpunkt, so wird Z = F · i · k und J = F · i², womit die Uebereinstimmung unsrer Ellipse mit der analytisch abgeleiteten Trägheitsellipse nachgewiesen ist.

Literatur: Culmann, Graph. Statik, Zürich 1875, Guidi, Lezioni di Statica graf., Torino 1886/87; Ritter, W., Schweiz. Bauzeitung 1888, Bd. 11, S. 121.

(† W. Ritter) Mörsch.

Fig. 1., Fig. 2.

Fig. 3., Fig. 4.