- Elastizitätsellipse
Elastizitätsellipse, eine Hilfskurve bei Lösung von Aufgaben aus der Baustatik.
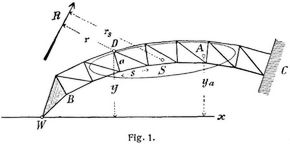
An dem linken Ende des rechts eingespannten Fachwerkträgers B C (Fig. 1) greife die Kraft R an. Dann wirkt im dritten unteren Gurtstäbe die Kraft U = R r : a (vgl. Momentenverfahren). Infolge seiner Elastizität verlängert sich der Stab um die Strecke Δ s = U s : E F (E = Elastizitätsmodul, F = Querschnittsfläche des Stabes). Denkt man sich die übrigen Stäbe unelastisch, so dreht sich der linke Fachwerkteil um den Punkt D. Der Drehungswinkel ist Δ δ = Δ s : a = R s r : E F a2. Setzt man: s/E F a2 = Δ g, so wird Δ δ = R · r · Δ g. Infolge dieser Drehung verschiebt sich der mit dem linken Fachwerksende in starrer Verbindung gedachte Punkt W in der Richtung Wx um die Strecke x =y · Δ δ = R · r · y · Δ g. Faßt man Δ g als ein Gewicht (»elastisches Gewicht«) auf, das im Punkte D angreift, so ist r · Δ g das statische Moment dieses Gewichtes, bezogen auf die Richtung der Kraft R, und r · y · Δ g dessen Zentrifugalmoment, bezogen auf die Kraft- und die Verschiebungsrichtung. Denkt man sich nun sämtliche Gurtstäbe elastisch, berechnet für jeden das Gewicht Δ g und belastet sämtliche Drehpunkte mit den ihnen zukommenden Gewichten, so ist der gesamte Drehungswinkel des linken Endes B gleich der Kraft R mal dem auf die Kraftrichtung bezogenen statischen Moment aller Gewichte und die gesamte Verschiebung des Punktes W gleich der Kraft R mal dem auf die Kraftrichtung und die Verschiebungsrichtung bezogenen Zentrifugalmoment aller Gewichte. Bestimmt man (Fig. 1) für sämtliche Gewichte den Schwerpunkt S und die Trägheitsellipse (s.d.) und setzt Σ (Δ g) = g, so wird der Gesamtdrehungswinkel δ = R rs g und die Gesamtverschiebung, wenn A der Antipol der Kraft ist, x = R rs yα g. Die so entstandene Ellipse heißt Elastizitätsellipse.
Legt man die x-Achse durch A, so wird die Verschiebung null; der Punkt W bewegt sich somit senkrecht zu W A, und seine Verschiebung kann als eine Drehung um den Antipol A angesehen werden. Fallen Kraft- und Verschiebungsrichtung zusammen, so geht das Zentrifugalmoment in das Trägheitsmoment über. Spannt man das linke Ende des Fachwerks ein und läßt das rechte freischweben, so gelangt man offenbar zu denselben Gewichten. Die Gewichtssumme g, der Schwerpunkt S und die Elastizitätsellipse sind daher von der Lagerung des Fachwerks unabhängig.
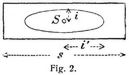
Auch für vollwandige Träger lassen sich Elastizitätsellipsen zeichnen. Man teilt den Träger zu diesem Zwecke in einzelne Elemente, bestimmt für jedes von ihnen das elastische Gewicht und die Elastizitätsellipse und setzt diese Gewichte nach den für Trägheitsellipsen geltenden Regeln zusammen. Für ein einzelnes Element (Fig. 2) ist das elastische Gewicht Δ g = s : E J, wo J das Trägheitsmoment des Querschnitts bezeichnet. Ferner ist
gleich dem Trägheitshalbmesser des Querschnitts und
worin G den Gleitmodul und F' eine Fläche bezeichnet, die stets kleiner ist als die Querschnittsfläche F des Trägers, bei rechteckigem Querschnitt ist F' = 5/6F, bei kreisförmigem gleich 27/32F, bei I-förmigem Querschnitt gleich der Fläche des Steges (vgl. Biegungslinie). Wird der Einfluß der Scherspannungen vernachlässigt, so ist einfacher i' = √1/32s. Mit Hilfe dieser Angaben lassen sich auch leicht Träger behandeln, die teils fachwerkförmig, teils vollwandig gebaut sind.
Die Elastizitätsellipsen leisten bei verschiedenen Aufgaben aus der Baustatik nützliche Dienste, so bei der graphischen Berechnung von Bogenträgern (s.d.), bei der Berechnung von Brückenpfeilern, bei der Bestimmung von Durchbiegungen u.s.w.
Literatur: Culmann, Graphische Statik, 2. Aufl., Zürich 1875; Ritter, Anwendungen der graphischen Statik, Teil 1, S. 150; Teil 2, S. 112, Zürich 1888–90.
(Ritter) Mörsch.
http://www.zeno.org/Lueger-1904.