- Beleuchtungskonstruktionen
Beleuchtungskonstruktionen. Bei der konstruktiven Darstellung der Beleuchtung der Oberfläche eines Körpers kommt nur die geometrische, nicht aber deren physikalische Beschaffenheit in Betracht; man spricht daher von einer geometrischen Beleuchtung, im Gegensatz zu der natürlichen Beleuchtung eines Körpers. Sind parallele Lichtstrahlen vorausgesetzt, so ist die Beleuchtungsstärke eines Flächenelementes proportional dem Cosinus des Neigungswinkels α der Normalen zum Flächenelement mit der Lichtrichtung, Lambertsches Gesetz. In allen Flächenelementen, in denen die Normalen senkrecht flehen zur Lichtrichtung, findet die Beleuchtung Null statt; die Verbindung aller dieser Stellen bildet die Selbstschattengrenze des Körpers. Sie teilt dessen Oberfläche in zwei Teile, von denen der der Lichtquelle zugekehrte Teil von dieser beleuchtet wird und der direkt beleuchtete Teil der Oberfläche heißt, während der andre im Schatten sich befindet und kein direktes Licht, wohl aber indirektes, sogenanntes Reflexlicht erhält. Die höchste Beleuchtung findet in jenen Flächenelementen statt, in denen die Flächennormalen zur Lichtrichtung parallel laufen; es sind dies im allgemeinen[680] nur einzelne Punkte der Oberfläche. Verbindet man alle gleichstark beleuchteten Punkte einer Oberfläche miteinander, so erhält man eine Linie gleicher Lichtstärke, eine Isophote. Die Aufgabe der Beleuchtungskonstruktionslehre besteht nun darin, für vorgegebene Werte von cos α, in der Regel 0, 0,1, 0,2, 0,3 .... 1,0 die zugehörigen Isophoten zu bestimmen, was darauf hinausläuft, senkrecht zu den Mantellinien eines senkrechten Kreiskegels, dessen Achse parallel zur Lichtrichtung und dessen Oeffnungswinkel α ist, die möglichen Tangentialebenen an die Oberfläche zu konstruieren. Die Verbindungslinie der Berührungspunkte dieser Tangentialebenen mit der beleuchteten Oberfläche gibt die dem Winkel α entsprechende Isophote ([1]–[7]).
Die Gesamtheit der genannten Tangentialebenen bildet eine der in Rede stehenden Oberfläche umschriebene Böschungsfläche, und es bilden die den Werten von cos α entsprechenden Isophoten ein Isophotensystem der Oberfläche. Man unterscheidet ein Isophotensystem im direkt beleuchteten Teile und ein solches im Selbstschauen, letzteres herrührend von der die Reflexbeleuchtung bewirkenden Lichtquelle. Durch das Isophotensystem wird die Oberfläche eines Körpers in eine Anzahl von Streifen geteilt und eine bildliche Darstellung der Beleuchtung dadurch erzielt, daß man die einzelnen Streifen mit einem Tusch- oder Farbtöne überlegt, dessen Stärke umgekehrt proportional ist der Beleuchtungsstärke des betreffenden Streifens.
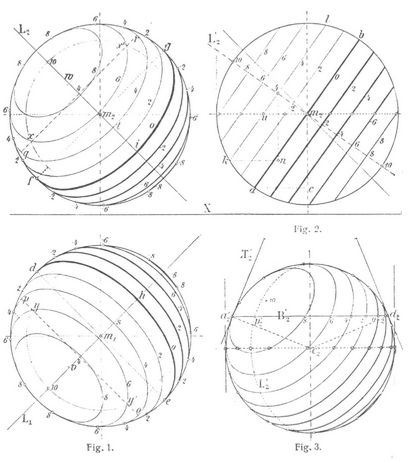
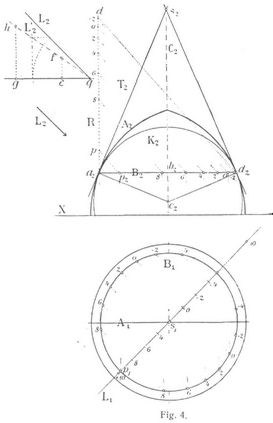
Für die Kugeloberfläche bestehen die Isophoten aus Kreislinien, deren Ebenen senkrecht flehen zur gewählten Lichtrichtung. Ist diese (Fig. 1) durch eine Gerade L gegeben, so erhält man mittels einer Seitenprojektion in eine zur Lichtrichtung parallele und zur Parallelebene E1 senkrechte Ebene, in der die Lichtrichtung unter ihrem wahren Winkel zur Parallelebene Ei geneigt erscheint, die Isophoten als die zu L2' senkrechten Kreissehnen durch Teilung des Durchmessers 10 · 10. Im Auf- und Grundriß stellen sich die Isophoten als Ellipsen dar, deren große Achsen bezw. senkrecht flehen zum Auf- und Grundriß der Lichtrichtung und deren Längen jenen der bezüglichen Kreissehnen in Fig. 2 gleich sind, z.B. für die Isophote 4 ist po im Grundriß Fig. 1 gleich qr im Aufriß Fig. 1 gleich lk im Seitenriß Fig. 2. Die kleinen Achsen fallen mit dem zur Lichtrichtung parallelen Kugeldurchmesser zusammen, und ihre Längen sind gleich den Projektionen der Kreissehnen Fig. 2 auf die Horizontale; so ist z.B. für die Isophote 4 die Länge der kleinen Ellipsenhalbachse gleich der Strecke kn in Fig. 2. Die Berührungspunkte der Isophoten mit dem zweiten und ersten Kugelumriß ergeben sich durch Uebertragung der Schnittpunkte des Isophotensystems der Seitenprojektion mit dem horizontalen Kugeldurchmesser auf den zur Lichtrichtung parallelen Durchmesser L2 bezw. L1 und Ziehen von Senkrechten zu diesen Linien durch die zugehörigen Teilpunkte; so ist für die Isophote 4 : m2ω = m1v = m2u. Die Senkrechten durch ω und v zu L2 bezw. L1 liefern auf dem Kugelumriß die Berührungspunkte 4.
[681] Für alle Flächen, deren geometrisches Bildungsgesetz bekannt ist, lassen sich aus letzterem direkte Isophotenkonstruktionen ableiten [3]. Vielfach verwendet man aber das Isophotensystem der Kugelfläche als Grundlage für die Ermittlung der Isophoten für irgend eine andre Oberfläche. Man braucht zu diesem Zwecke ja nur längs der Punkte der Kugelisophoten Tangentialebenen an die Kugel zu legen und diese parallel bis zur Berührung mit der in Rede stehenden Oberfläche zu verschieben; ihre Berührungspunkte gehören dann dem Isophotensystem der Fläche an. Besonders einfach gestalten sich die Konstruktionen für den senkrechten Kreiszylinder, Kreiskegel und die Umdrehungsflächen. Jedem senkrechten Kreiszylinder bezw. Kreiskegel läßt sich eine nach dem Grundkreise berührende Kugel einbeschreiben, deren Isophotensystem den Grundkreis von Zylinder bezw. Kegel nach Punkten schneidet, durch welche die zugehörigen Isophoten als Mantellinien hindurchgehen (s. Fig. 3).
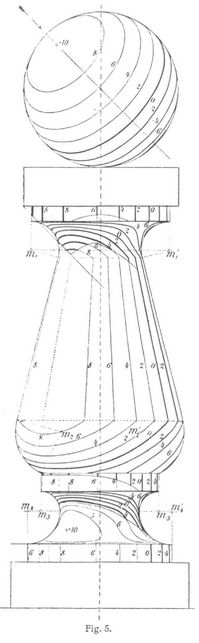
An einer Umdrehungsfläche gibt es für jeden Parallelkreis, z.B. B (s. Fig. 4) einen die Oberfläche nach diesem Parallelkreise berührenden Kegel. Verschafft man sich zu diesem für eine gegebene Kugel (s. Fig. 3) einen die letztere berührenden Parallelkegel, so liefert dieser auf der Kugel einen Kreis B' dessen Aufriß in Fig. 3 durch B2' dargestellt ist und der das Isophotensystem der Kugel durchschneidet. Die hierdurch entstehende Teilung auf B2' ist proportional auf B2 (Fig. 4) zu übertragen. Aus dein Aufriß ergeben sich durch Herabprojizieren die Isophoten auf B1 im Grundriß. Durch Annahme beliebig vieler Parallelkreise lassen sich hinlänglich viele Punkte des Isophotensystems der Umdrehungsfläche konstruieren. In Fig. 5 ist das Isophotensys für eine Umdrehungsfläche dargestellt.
Im Gegensatz zur geometrischen wahren Beleuchtung fleht die scheinbare Beleuchtung eines Körpers; hierbei ist Rücksicht genommen auf den Standpunkt des Beobachters und auf das Reflexionsvermögen der beleuchteten Oberfläche. Unter der Annahme, daß die vom Beobachter, der in unendlicher Ferne senkrecht zur bezüglichen Projektionsebene vorausgesetzt ist, wahrgenommene Beleuchtung proportional ist dem Cosinusprodukte cosα ∙ cosβ, unter β den Winkel der Sehrichtung verstanden, kann man auch Linien gleicher scheinbarer Beleuchtung [3] konstruieren, indem man alle jene Punkte der Oberfläche aufsucht, für die das genannte Cosinusprodukt denselben Wert besitzt. Eine Verbindungslinie dieser Punkte kann man eine Linie gleicher Helle (Isophenge) nennen und demgemäß ein Isophengensystem der Oberfläche konstruieren. – Da aber der Beobachter niemals den vorstehend bezeichneten Standpunkt einnimmt, so hat die konstruktive Darstellung dieser scheinbaren Beleuchtung keinen praktischen Wert. – Für praktische Zwecke genügt die Darstellung der wahren geometrischen Beleuchtung vollständig.
Literatur: [1] Tilscher, Geometrische Beleuchtungskonstruktionen, Wien 1862. – [2] Koutny, Theorie der Beleuchtung krummer Flächen 2. Grades bei parallelen Lichtstrahlen, Brunn 1867. – [3] Burmester, Theorie und Darstellung der Beleuchtung gesetzmäßig gestalteter Oberflächen, Leipzig 1871. – [4] Tessare, La teoria delle ombre e del chiaro-scuro, Torino 1878–80. – [5] Fiedler, Darstellende Geometrie, Leipzig 1871. – [6] Wiener, Darstellende Geometrie, ebend. 1884. – [7] Vonderlinn, Ueber die Konstruktion der Selbst- und Schlagschattengrenzen, sowie der Linien gleicher Beleuchtungsstärke an Rotationsflächen, in Zeitschr. für deutsche Zeichenlehrer 1889–91. – [8] Schattierungskunde von Rieß.
Vonderlinn.
http://www.zeno.org/Lueger-1904.