Biegungslinie

Biegungslinie, auch Durchbiegungslinie, elastische Linie, Biegungspolygon genannt, heißt in der Statik der Bauwerke die Linie, in die infolge der Elastizität des Baustoffes die Achse eines ursprünglich geradlinigen Balkenträgers unter dem Einfluß von belaufenden Kräften übergeht. Die größte Abweichung der Biegungslinie von der ursprünglichen Trägerachse heißt Biegungspfeil. Auch bei krummlinigen oder Bogenträgern kann man von Biegungslinie sprechen. Man verlieht darunter die Kurve, die man erhält, wenn man die elastischen Verschiebungen, welche die Trägerachse in irgend einer Richtung ausführt, von einer auf dieser Richtung senkrecht stehenden Linie aus aufträgt. Die Biegungslinie ist teils von den Biegungsmomenten, teils von den Querkräften abhängig. Man bestimmt am einfachsten beide Einflüsse gesondert und addiert sie nachher.

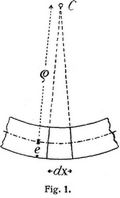
Einfluß der Biegungsmomente: Steht ein ursprünglich rechteckiges Balkenelement unter dem Einfluß eines Biegungsmomentes M, so nimmt es eine trapezförmige Gestalt an (vgl. Fig. 1). Die ursprünglich parallel zueinander laufenden Querschnitte schneiden sich jetzt im Punkte C. Die Entfernung ρ dieses Punktes von der Balkenachse ist der Krümmungshalbmesser der Biegungslinie. Nach der Biegungstheorie ist die Spannung in der äußersten (untersten) Faser σ = eM/J, wenn J das Trägheitsmoment des Querschnitts bedeutet. Die Verlängerung dieser Faser ist nach der Theorie der Elastizität gleich ^σ/_Edx, wenn E den Elastizitätsmodul bedeutet. Diese Verlängerung verhält sich aus geometrischen Gründen zu e wie dx zu ρ; folglich ist

Da die Biegungslinie eine sehr flache Kurve ist, so darf man 1/ρ durch d²y/dx² ersetzen und findet dadurch die Differentialgleichung der Biegungslinie

[8] Sind M und J als Funktionen von x gegeben, so kann man hiernach die Gleichung der Biegungslinie und daraus den Biegungspfeil berechnen.

Die Differentialgleichung eines Seilpolygons für verteilte Belastung lautet:

d²y/dx² = p/h,

wenn p die Belastungsgröße und h die Polweite bezeichnet. Hieraus folgt, daß man die Biegungslinie auch als Seilpolygon auffassen und zeichnen kann: Man betrachtet die Biegungsmomente als Belastungen, mit andern Worten, die Momentenfläche als Belastungsfläche, und wählt das Produkt EJ als Polweite. Bei veränderlichem J bekommt man ein Kräftepolygon mit veränderlichem Pole (s. Summationspolygon). Zeichnet man die Momentenfläche mit der Polweite H und verwandelt sie, um das zweite Kräftepolygon zu erhalten, auf die Balis a, so ist p = M:Ha. Man muß daher h = EJ:Ha machen, wenn man die Biegungslinie in richtiger Größe erhalten will. Da jedoch die Biegungslinie, um deutlich zu werden, verzerrt gezeichnet werden muß, so nimmt man h stets viel kleiner an. Das Verzerrungsverhältnis ist alsdann gleich: EJ:Hah.

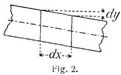
Einfluß der Querkräfte. Unter dem Einfluß der Querkräfte Q gehen die ursprünglich rechteckigen Balkenelemente in parallelogrammförmige über (Fig. 2). Zwei um dx voneinander entfernte Querschnitte verschieben sich gegenseitig um die Strecke dy = Qdx:GF', worin G den Gleitmodul und F' eine Fläche bedeutet, die stets kleiner ist als die Querschnittsfläche F des Balkens. (Bei rechteckigem Querschnitt ist F' = ⁵/₆ F, bei kreisförmigem = ²⁷/₃₂ F, bei I-Querschnitten gleich der Fläche des Steges). Daraus folgt als Gleichung der Biegungslinie

dy/dx = Q/GF' oder da Q = dM/dx, y = M/GF'.

Ist die Momentenfläche mit der Polweite H gezeichnet, so hat man demnach ihre Ordinaten einfach mit H:GF' zu multiplizieren, um den Einfluß der Querkräfte auf die Biegungslinie zu erhalten. Handelt es sich nicht darum, die wirklichen Durchbiegungen eines Balkens zu berechnen (wie es z.B. bei Belastungsproben geschieht), sondern dient die Biegungslinie als Hilfsmittel zur statischen Berechnung von Bauwerken (z.B. von durchlaufenden Balken), so kann der Einfluß der Querkräfte in der Regel vernachlässigt werden.

Soll die Biegungslinie eines Fachwerkträgers berechnet werden, so ersetzt man bei parallelen Gurtungen und einfachem Strebenzuge J durch ¹/₂F_gh² und GF' durch EF_s cos α sin g²α, worin F_g den Querschnitt der Gurtung, h die Fachwerkshöhe, Fs den Querschnitt der Strebe und α ihren Neigungswinkel bezeichnet. Bei veränderlichen Querschnitten werden passende Mittelwerte eingeführt. Bei mehrfachem Strebenzug ist Fs entsprechend zu multiplizieren. Ist die Fachwerkshöhe veränderlich, so ist in der Regel ein zeichnerisches Verfahren vorzuziehen. Der Formänderungswinkel für einen einzelnen Fachwerksstab ist Ms : EFa² (M = Drehpunktsmoment, s = Stablänge, F = Stabquerschnitt, a = Abstand des Stabes vom Drehpunkte). Man betrachtet am besten die M als Kräfte, die in den Drehpunkten angreifen, und setzt sie durch ein Seilpolygon zusammen, wobei man die Größen EFa² : s als Polweiten verwendet. Da die Drehpunkte der Streben meist außerhalb der Spannweite oder gar unendlich fern liegen, so ersetzt man deren Kräfte gewöhnlich durch je zwei in der Nähe des betreffenden Faches liegende Kräfte. In manchen Fällen darf der Einfluß der Streben vernachlässigt werden, was die Zeichnung wesentlich erleichtert. Ein andres Verfahren besteht darin, daß man die Formänderungswinkel zahlenmäßig berechnet, für jeden Knotenpunkt der geradlinigen Gurtung addiert und die Summen, als Kräfte betrachtet, durch ein Seilpolygon zusammensetzt. Auch das Williotsche Formänderungspolygon sowie die Sätze von den virtuellen Verschiebungen und von den Elastizitätsellipsen können zur Bestimmung der Biegungslinie eines Fachwerkträgers benutzt werden.

Soll die Durchbiegung eines Balkens an einer bestimmten Stelle für veränderliche Belastungen berechnet werden, so zeichnet man am besten die Biegungslinie für eine an dieser Stelle angreifende Einzellast. Dann stellt diese Linie nach dem Gesetze von der Gegenseitigkeit der Formänderungen die Einflußlinie für die Durchbiegung des Balkens dar.

Literatur: [1] Ritter, W., Anwendungen der graphischen Statik, 1. Teil, 4. Kap., und 2. Teil, 3. Kap., Zürich 1888–90. – [2] Müller-Breslau, Graphische Statik der Baukonstruktionen, 2. Bd., Leipzig 1892. – [3] Bach, C., Elastizität und Fertigkeit, 4. Aufl., Berlin 1902. – [4] Land, R., Zeitschr. für Bauwesen 1894, S. 611. – [5] Fopp I, A., Vorlesungen über technische Mechanik, Bd. 2 und 3, Leipzig 1900.

(W. Ritter) Roth.

Fig. 1.

Fig. 2.