Fachwerke, durchlaufende

Fachwerke, durchlaufende. (Graphische Berechnung.)

Zur statischen Berechnung durchlaufender Fachwerke verwendet man meistens die Verfahren und Regeln, die bei der Berechnung durchlaufender Balken (s. Bd. 1, S. 513) üblich sind. Man zeichnet die Kurven der größten und kleinsten Biegungsmomente sowie die Kurven der größten und kleinsten Querkräfte und berechnet aus jenen die Gurtungskräfte, aus diesen die Strebenkräfte (vgl. Parallelträger). Dieses Verfahren ist für die Praxis hinreichend genau, solange die Gurtungen parallel laufen. Trifft dies jedoch nicht zu, so wird die Berechnung am übersichtlichsten, wenn man für die verschiedenen Stäbe Einflußlinien (s.d.) zeichnet.

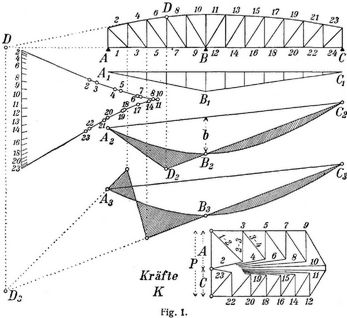
Handelt es sich um ein Fachwerk mit zwei Oeffnungen (Fig. 1), so setzt sich die Einflußfläche für einen Stab aus zwei Flächen zusammen. Die eine entsteht, wenn man die Stütze B entfernt denkt, also das Fachwerk statisch bestimmt macht; die andre, wenn man den Stützendruck B allein in Betracht zieht. Beide Flächen voneinander abgezogen, ergeben die Einflußfläche für den betreffenden Stab. Für den Gurtungsstab 7 z.B. hat die Einflußfläche die Form A₂ B₂ C₂ D₂. Das Dreieck A₂ D₂ C₂ entspricht dem in beiden Endpunkten aufliegenden Fachwerkträger (S. 233), die Kurve A₂ B₂ C₂ dem Stützendrucke B. Diese Kurve ist nichts andres als die Biegungslinie (s.d.) für die Kraft B. Man zeichnet die dreieckige Momentenfläche A₁B₁C₁ (Höhe beliebig), betrachtet die Momente als Kräfte, die in den Drehpunkten der Stäbe angreifen, und setzt sie durch ein Kräfte- und ein Seileck zusammen. Das Krafteck ist Fig. 1 links gezeichnet. Als Kräfte sind die halben Momentenordinaten aufgetragen. Als Polweiten verwendet man, in beliebigem Maßstabe aufgetragen, die Größen Fa² : s, worin F die Querschnittsfläche des Stabes, a seinen Abstand vom Drehpunkte und s seine Länge bedeutet. Der Formänderungswinkel (s.d.) ist nämlich allgemein gleich Ms : EFa², so daß man die Biegungslinie erhält, wenn man M als Kraft und Fa² : s als Polweite annimmt. Den Elastizitätskoeffizienten E setzt man gleich Eins, da der Maßstab, in dem die Biegungslinie gezeichnet wird gleichgültig ist. Man darf sich bei dieser Arbeit auf die Gurtungsstäbe beschränken und die Formänderung der Streben vernachlässigen. Hat man die Biegungslinie A₂ B₂ C₂ gezeichnet, so ist es leicht, die gebrochene Linie A₂ D₂ C₂ zu zeichnen, denn beide Linien müssen sich in B₂ schneiden, weil eine Last im Auflager B keinen Einfluß auf die Stabkraft ausübt.– In gleicher Weise gelangt man zu einer Einflußfläche für eine Strebe. A₃ B₃ C₃ stellt diese Fläche für die Strebe 3/4 dar. – Unten auf Fig. 1 sind mittels eines Cremonaschen Planes die Stabkräfte K für eine in B angreifende Last P gezeichnet. Man wählt als solche die am häufigsten vorkommende Einzellast, bei Eisenbahnbrücken das Gewicht eines Lokomotivrades, bei Straßenbrücken die Verkehrslast pro Feld. Nennt man die Ordinaten der Einflußfläche z, so ist schließlich die gesuchte Stabkraft S = KΣ(z) : b.

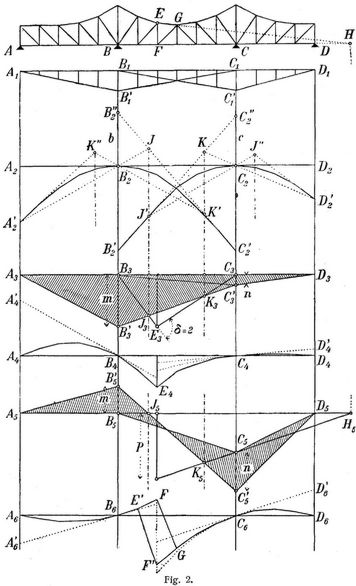
Erstreckt sich das Fachwerk über mehr als zwei Oeffnungen, so wird dessen Berechnung umständlicher. Unter den verschiedenen Verfahren, die hier in Frage kommen, dürfte das folgende eines der bequemsten und übersichtlichsten sein. Man zeichnet (Fig. 2) die dreieckige Momentenfläche A₁ B₁' C₁ und dazu, indem man die Momentenordinaten als Kräfte und[542] die Werte Fa² : s als Polweiten betrachtet, das Seileck A₂' B₂ C₂'. In gleicher Weise zeichnet man für die Strecke BD das Seileck B₂' C₂ D₂'. (Die Kraftecke sind aus der Figur weggelassen.) Die geraden Linien A₂' B₂ und D₂' C₂ führen zu den Fest- oder Inflexionslinien (vgl. Bd. 1, S. 516) J und K der Mittelöffnung, die Linien J' C₂ und K' B₂ zu denen der Außenöffnungen. Um die Einflußfläche für den 7. unteren Gurtstab zu erhalten, zieht man aus B₃ und C₃ zwei Linien, die sich lotrecht unter dem Drehpunkt E schneiden (vgl. Bd. 3, S. 233, Fig. 2). Den Knickwinkel B₃ E₃ C₃ macht man σ = 1 oder = 2, zieht die Linien B₃' J₃ K₃ C₃', B₃' A₃ und C₃' D₃ und zeichnet für die schraffierte Fläche, indem man sie als Momentenfläche betrachtet, die Biegungslinien A₄ B₄ E₄ und D₄ C₄ E₄. Hierzu verwendet man die bereits gezeichneten Linien A₂' B₂ C₂' und B₂' C₂ D₂'; und zwar sind bloß deren Ordinaten im Verhältnis m : b bezw. n : c zu verkleinern, was mittels zweier Verwandlungswinkel rasch geschehen kann. Man beginnt damit, A₂ A₂' und A₄ A₄' zu verwandeln, die Gerade A₄' B₄ zu ziehen und von ihr aus die verwandelten Ordinaten der Kurve A'₂ B₂ C'₂ aufzutragen. Sie entsprechen der Momentenfläche A₃ B₃' C₃'. Von B₄ aus fügt man noch weitere Ordinaten an, die der Momentenfläche B₃ C₃' D₃ entsprechen; es sind die im Verhältnis n : c verwandelten Ordinaten zwischen der Kurve B₂' C₂ und der Geraden B₂' C₂''. Diese Arbeit wird bis E₄ fortgesetzt. Dann wiederholt man sie, von D₄ ausgehend, für die rechts von E liegende Fläche, wobei man ebenfalls auf den Punkt E gelangt. Zuerst wird D₄ D₄' = (n : c) D₂ D₂' aufgetragen und die Gerade D₄' C₄ gezogen. Von dieser aus trägt man die im Verhältnis n : c verwandelten Ordinaten der Kurve D₂' C₂ B₂' auf und von C₄ aus fügt man noch die im Verhältnis m : b verwandelten Ordinaten zwischen der Geraden C₂' B₂'' und der Kurve C₂' B₂ an. Nennt man die Ordinaten dieser Einflußlinien z und die Einzellast P, so ist (wegen δ = 2) Σ(Pz) das doppelte Biegungsmoment hinsichtlich des Drehpunktes E. – A₆ B₆ FG C₆ D₆ ist die Einflußfläche für die Strebe FG. Man trägt am besten die Einzellast P lotrecht unter dem Fußpunkte der Strebe auf (richtiger unter dem Punkte, in dem die Wagrechte durch H die Strebe trifft) und verbindet ihre Endpunkte mit dem lotrecht unter dem Drehpunkte der Strebe liegenden Punkte H₅. Dann zieht man J₅ K₅, B₅ C₆, A₆ B₅' und C₅' D₅ und erhält damit die schraffierte Fläche. Die dieser Fläche entsprechende Biegungslinie stellt die gesuchte Einflußlinie dar; ne wird ähnlich wie jene für die Gurtungen gezeichnet. Die Strebenkraft wird gefunden, wenn man Σ(z), im Maßstab der Kraft P abgegriffen, parallel zur Strebe und zur Wagrechten zerlegt. Die gezeichnete Einflußlinie gilt auch für den Pfosten EF; nur muß der Strich FG durch E'F' ersetzt werden. – Für Stäbe in den Außenöffnungen sind die nämlichen Wege einzuschlagen; die Zeichnung gestaltet sich dort noch etwas einfacher. Auch sonst ergeben sich, wenn man die Einflußlinien für sämtliche Stäbe zeichnet, da und dort Vereinfachungen. Ferner kann man die ganze Zeichnung bei symmetrischer Anordnung des Fachwerks selbstverständlich auf die Hälfte beschränken. Unschwer läßt sich das beschriebene Verfahren auf mehr als drei Oeffnungen ausdehnen.

Literatur: Schäffer und Sonne, Handbuch des Brückenbaus, Kap. 9, Leipzig 1890; v. Thuille, Einflußlinien für einen Fachwerkträger auf drei Stützen, Wochenschr. des österr. Ingen.- u. Arch.-[543] Ver. 1891; Müller-Breslau, Graphische Statik der Baukonstruktionen, Leipzig 1892; Klingatsch, Graphische Behandlung kontinuierlicher Fachwerkbalken, Zeitschr. des österr. Ingen.- u. Arch.- Ver. 1892; Zschetzsche, Beitrag zur Berechnung durchgehender Balkenträger, Zeitschr. f. Bau- Wesen 1894.

(W. Ritter) Mörsch.

Fig. 1.

Fig. 2.