- Doppelkurbelgetriebe
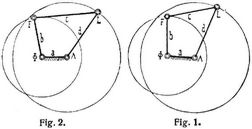
Doppelkurbelgetriebe. Zwei Kurbeln ΦF, ΔL (Fig. 1), die sich in dem festen Gestell ΦΔ resp. um die parallelen Achsen Φ, Δ drehen und durch eine Koppel F L vermittelst der ebenfalls parallelen Achsen F, L drehbar verbunden sind, bilden, wenn beide gekoppelte Kurbeln vollständige Umdrehungen vollziehen können, mit dem Gestell und der Koppel ein Doppelkurbelgetriebe [1], das auch Doppelkurbel und Kurbelkupplung [2] genannt wird.
Die vier durch vier Gelenke mit parallelen Achsen verbundenen Glieder, deren Längen mit a, b, c, d bezeichnet sind, bilden, geometrisch betrachtet, ein Gelenkviereck. Vollständige Umdrehungen der beiden Kurbeln Φ F, Δ L resp. b, d sind nur dann möglich, wenn die Summe der kleinsten Gliedlänge und der größten Gliedlänge nicht größer als die Summe der beiden andern Gliedlängen ist und das kürzeste Glied das feste Gestell vertritt. In Fig. 1 ist das kürzeste und feste Glied a, ferner d das größte Glied und a + d < b + c. Wenn insbesondere a + d = b + c[7] genommen wird, dann ist das Doppelkurbelgetriebe ein durchschlagendes, und alle vier Seiten des Gelenkvierecks liegen in der Durchschlagslage in der Geraden Φ Δ. In Fig. 2 ist wieder a das kleinste, aber c das größte Glied und a + c < b + d. Wenn insbesondere a + c = b + d, dann erhalten wir auch in diesem Fall ein durchschlagendes Doppelkurbelgetriebe, bei dem alle vier Seiten des Gelenkvierecks in der Durchschlagslage in der Geraden Φ Δ liegen. Dreht sich die eine Kurbel, z.B. Φ F, gleichförmig, so dreht sich die andre Kurbel Φ Δ ungleichförmig. Nur in dem speziellen Falle, wenn das Gelenkviereck Φ F L Δ ein Parallelogramm, also a = c, b = d ist, drehen sich beide Kurbeln in gleicher Weise, und wir erhalten dann das Parallelkurbelgetriebe (s.d.), das bei der Kupplung der Triebräder der Lokomotive angewendet wird.
Literatur: [1] Burmester, Lehrbuch der Kinematik, Leipzig 1888, Bd. 1, S. 290. – [2] Weisbach-Herrmann, Ingenieur und Maschinenmechanik, Braunschweig 1876, 2. Aufl., 3. Teil, 1. Abt, S. 665. – [3] Grashof, Theoretische Maschinenlehre, Leipzig 1883, Bd. 2, S. 114.
Burmester.
http://www.zeno.org/Lueger-1904.