Meßmethoden

Meßmethoden, elektrotechnische, dienen entweder zur Bestimmung nur elektrischer Größen und ihrer Beziehungen zueinander (Gruppe A.) oder solcher Größen, die zur Elektrotechnik in enger Beziehung stehen, nämlich der magnetischen Größen (Gruppe B.) sowie mechanischer und photometrischer Größen.

Hier sollen nur die Gruppen A. und B. besprochen werden; über die Messungen mechanischer Größen s. Dynamometer, über die photometrischen Messungen s. Photometrie.

A. Die elektrischen Meßmethoden

zerfallen I. in die Messungen einzelner elektrischer Größen und II. die Untersuchungen von Materialien, Apparaten und Maschinenanlagen, Elementen und Akkumulatoren (technische Messungen).

I. Zu den Größen, welche durch Meßmethoden bestimmt werden können, gehören 1. der Widerstand, 2. die Spannung und Stromstärke (Kompensationsmethoden), 3. der Effekt, 4. die Elektrizitätsmenge, 5. die Kapazität, 6. die Induktionskoeffizienten.

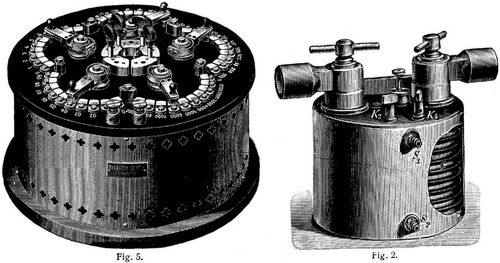
1. Widerstandsmessungen. Man mißt die Größe eines Widerstandes, indem man ihn mit einem Normalwiderstände vergleicht. Die Einheit des Widerstandes, 1 Ohm (Ω), ist der [382] Widerstand einer Quecksilbersäule von 106,3 cm Länge und 1 qmm Querschnitt bei 0°. Da diese Einheit sehr unbequem ist, stellt man Normalwiderstände aus Drähten von solchem Material her, das lieh mit der Temperatur nicht ändert (Manganin oder Konstanten) Die Drähte sind auf eine Messingbüchse aufgewickelt, die von einem vernickelten Messingmantel umschlossen ist, und stehen mit zwei starken Kupferbügeln in Verbindung. (Fig. 1 stellt einen Normalwiderstand von 100 Ω dar.) Beim Gebrauch wird das Ganze in ein Petroleumbad gehängt, wobei die Enden der Kupferbügel in Quecksilbernäpfe tauchen. Bei Widerständen für starke Ströme ist die Spule von einer Kühlschlange umgeben (Fig. 2 zeigt einen Normalwiderstand von 0,0001 Ω).

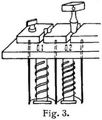
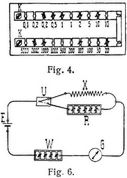
Die Meßwiderstände (Rheostaten) enthalten ganze Widerstandssätze, mit denen man jeden beliebigen Widerstand einschalten kann. Sie bestehen aus induktionsfrei (bifilar) gewickelten Spulen, welche in Kästen so angeordnet sind, daß man durch Ziehen oder Stecken von Metallstöpseln beliebig viele von ihnen einschalten kann. Fig. 3 zeigt einen Teil der inneren Anordnung, Fig. 4 den ganzen Kasten, von oben gesehen. Wenn die Stöpsel und Stöpsellöcher nicht sorgfältig gereinigt sind, können leicht erhebliche Fehler entstehen. Man hat deshalb Dekadenwiderstände angefertigt, bei welchen durch Stecken eines Stöpsels eine beliebige Anzahl von zehn gleichen Spulen eingeschaltet werden kann; für jede Dekade ist nur ein Stöpsel erforderlich. Die Dekadenwiderstände werden häufig auch als Kurbelrheostaten eingerichtet (Fig. 5 stellt einen Kurbelrheostaten von Siemens & Halske mit 160000 Ω dar).

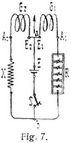
a) Substitutions-(oder Ersatz-)Methode. Man schaltet den unbekannten Widerstand X mit einem Galvanometer G in den Stromkreis eines Elementes E ein und beobachtet den Ausschlag α. Dann ersetzt man mittels eines Umschalters U den unbekannten Widerstand durch einen Rheostaten (Fig. 6) und schaltet in diesem einen solchen Widerstand R ein, daß man wieder den Ausschlag α erhält. Dann ist X = R. Das Resultat ist nur richtig, wenn E konstant blieb. Die Stromstärke darf daher nur sehr klein sein, und man wendet diese Methode nur zur Messung sehr großer Widerstände, z.B. bei Isolationsmessungen, an.

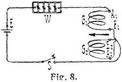
b) Widerstandsmessung mit dem Differentialgalvanometer. Man kann sich von der Konstanz des Elementes unabhängig machen, wenn man X und den Rheostaten gleichzeitig einschaltet, parallel zueinander, mit je einer Spule des Galvanometers verbunden (Fig. 7). Hat man im Rheostaten R Ω einschalten müssen, um das Galvanometer auf Null zu bringen, so ist X = R, wenn beide Spulen gleichen Widerstand besitzen. Ist das nicht der Fall, so[383] kann man den Widerstand der Spulen eliminieren, indem man die Verbindung von X und R mit den Spulen vertauscht (mittels eines Umschalters). Hat man zuerst R₁Ω, nach der Vertauschung R₂Ω einschalten müssen, so ist X = (R₁ + R₂) : 2. Muß das Galvanometer zunächst justiert, also so eingestellt werden, daß gleiche Ströme sich gerade aufheben, so schickt man ein und denselben Strom in entgegengesetztem Sinne durch die Spulen und verschiebt sie, bis der Ausschlag gleich Null ist (Fig. 8).

c) Widerstandsmessung nach dem Ohmschen Gesetz. Man schickt durch x einen Strom und mißt die Stromstärke i sowie die Spannung e an den Klemmen von x, dann ist x = e/i. (Angewendet zu Widerstandsmessungen an Dynamomaschinen, bei brennenden Glühlampen u.s.w.)

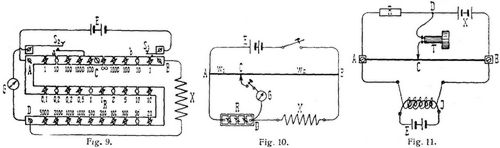
d) Widerstandsmessungen mit der Wheatstoneschen Brücke. Verbindet man vier Widerstände w₁, w₂, w₃ und w₄ zu einem Viereck, schaltet an zwei gegenüberliegende Punkte ein Element, an die beiden andern Punkte ein Galvanometer, so sind die Produkte der gegenüberliegenden Widerstände einander gleich, w₁ w₄ = w₂ w₃ oder w₁ : w₂ = w₃ : w₄, sobald das Galvanometer stromlos ist (Wheatstonesche Brücke). Schaltet man X in den Zweig w₄, in die andern Zweige bekannte Widerstände und gleicht diese so ab, daß das Galvanometer keinen Ausschlag gibt, so ist X = w₂/w₁ w₃. Bei der Abgleichung genügt es, nur den einen Widerstand zu ändern, z.B. w₃ während das Verhältnis w₂/w₁ konstant bleibt. Man braucht dann nur einen vollständigen Rheostaten, während für die Verhältniswiderstände w₁ und w₂ je eine Spule genügen würde. Man hat besondere Kästen angefertigt, welche in der Mitte eine Abzweigklemme C und beiderseits solche Widerstände besitzen, daß das Verhältnis w₂/w₁ = b/a einen bequemen Wert hat, z.B. 1; 10; 0,1 u.s.w. Hat man im Rheostaten RΩ eingeschaltet und dadurch G stromlos gemacht, so ist X = b/a R (Stöpselbrücken). Wenn man die Verhältniswiderstände a und b mit dem Rheostaten in einem Kasten vereinigt, erhält man einen Universalwiderstandskasten (Fig. 9). – Man kann die Abgleichung auch dadurch bewirken, daß man das Verhältnis b/a ändert, während R konstant bleibt. Man nimmt dann für die Verhältniswiderstände die Teile eines homogenen Drahtes, an welchem ein verschiebbarer Kontakt angebracht ist. Für R genügt dann ein Karten mit einigen Spulen von bequemem Wert, z.B. 0,1 Ω, 1 Ω, 10 Ω u.s.w. (Drahtbrücken, Fig. 10). Hat man durch Verschieben des Kontaktes G stromlos gemacht, so ist wieder X = w₂/w R = b/a R. Da aber a und b sich wie die Drahtlängen l₁ und l₂ verhalten, so ist auch X = l₂/l₁ · R; z.B. R = 1 Ω · l₁ = 28 cm; l₂ = 100 – 28, also X = 72/28 · 1 = 2,57 Ω.

Eine handlichere Form der Wheatstoneschen Brücke erhält man, wenn man den Draht kreisförmig ausspannt; die Skala kann dann eine Gradteilung erhalten. Statt der Längen- oder Gradteilung kann man aber auch eine Teilung anbringen, die sofort das Verhältnis b : a abzulesen gestattet.

Für besondere Zwecke erhält die Wheatstonesche Brücke nach Anordnung oder Methode bestimmte Abänderungen. Zur Messung des Widerstandes von Flüssigkeiten und Elementen verwendet man zur Vermeidung der Polarisation Wechselstrom (z.B. aus einem Induktionsapparat), statt des Galvanometers ein Telephon. Will man mit einer Telephonmeßbrücke den Widerstand von Elementen messen, so muß man deren elektromotorische Kraft unwirksam machen. Man schaltet deshalb zwei Elemente gegeneinander in den Zweig w₄ ein und mißt die Summe ihrer Widerstände. Man nimmt dann noch ein drittes Element hinzu und mißt es mit dem ersten und dann mit dem zweiten Element zusammen. Aus drei Gleichungen erhält man die drei Widerstände einzeln.

Mit den Telephonmeßbrücken kann man auch die Widerstände fester Leiter messen mit Ausnahme von Induktionswiderständen (z.B. Widerständen an Maschinen). Zu Blitzableiteruntersuchungen verwendet man meist Telephonmeßbrücken, die mit den Vergleichswiderständen R, dem Induktionsapparat und Trockenelementen in einen transportabeln Karten eingebaut sind.

[384] Zur Bestimmung des spezifischen Widerstandes einer Flüssigkeit tut man diese in ein Gefäß, dessen Dimensionen leicht meßbar sind, z. B in eine zylindrische Röhre. Man kann dann auch mit Gleichstrom messen und eliminiert den Einfluß der Polarisation, indem man bei zwei verschiedenen Längen der Flüssigkeitssäule, l₁ und l₂, den Widerstand mißt. Durch Subtraktion erhält man den Widerstand für die Länge l₁ – l₂. Kann man die Dimensionen des Gefäßes nicht ausmessen, so mißt man mit demselben Gefäß auch den Widerstand einer Flüssigkeit, deren spezifischer Widerstand bekannt ist. Die spezifischen Widerstände verhalten sich dann wie die gemessenen Widerstände.

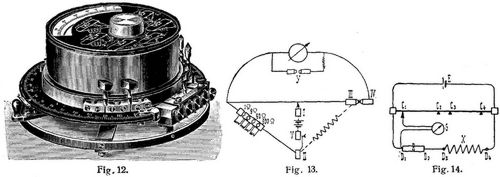
Zu Widerstandsmessungen läßt sich bequem das Universalgalvanometer von Siemens & Halske verwenden, welches aus einem einohmigen Spulengalvanometer, einer runden Drahtbrücke mit Schleifkontakt und einem Rheostaten mit 1, 9, 90 und 900 Ω nebst erforderlichen Verbindungen und Klemmschrauben besteht. Fig. 12 zeigt das Aeußere, Fig. 13 die Schaltung des Apparates (ausgezogene Linien) und seine Verwendung zu Widerstandsmessungen (punktierte Linien). – Der Meßdraht umfaßt 300° der kreisförmigen Schieferplatte, die Skala ist bei dem alten Universalgalvanometer von der Mitte an beiderseits in 150° geteilt; die beiden Seiten sind mit A und B bezeichnet. Hat man α° Grad auf der A-Seite abgelesen, so ist X = (150 + α/150 – α)R, dagegen bei Ablesungen auf der B-Seite X = (150 – α/150 + α)R. – Bei den neueren Instrumenten liest man sofort das Verhältnis ab

Bei der Messung kleiner Widerstände können die Verbindungsdrähte zu ungenauen Messungen Anlaß geben, man soll sie daher möglichst kurz und dick wählen. Man kann den Fehler nach der Methode von Matthiesen & Hockin eliminieren, indem man das Galvanometer nicht mit der Verbindungsstelle von X und R verbindet, sondern nacheinander an die vier Punkte D₁, D₂, D₃ und D₄ (die Klemmen von R und X) legt und die vier Punkte C₁, C₂ C₃ und C₄ auf dem Drahte bestimmt, bei welchen das Galvanometer keinen Ausschlag gibt (Fig. 14). Ist l₁ die Drahtlänge zwischen C₁ und C₂, l₂ die Länge zwischen C₃ und C₄ so ist X = l₂/l₁ R.

Zur Messung kleiner Widerstände dient auch die Thomsonsche Doppelbrücke von Siemens & Halske (in Fig. 15 schematisch dargestellt), welche zur Messung von Widerständen von 0,1–0,000001 Ohm benutzt werden kann. Zur Messung kurzer Drahtstücke, Lichtkohlen u. dergl. ist eine besondere Einspannvorrichtung vorhanden. Als Vergleichswiderstand R dient ein kreisförmig ausgespannter Meßdraht D (mit dem Schleifkontakt e) von 0,01 Ohm Widerstand, der mit dem unbekannten Widerstand X in den Hauptstromkreis H K eingeschaltet ist. Von dem Meßdraht und von X sind je zwei Drähte nach den Widerstandssätzen w₃ – w₄ und w₅ – w₆ abgezweigt, zwischen welchen das Galvanometer G liegt. Man wählt die Verhältnisse w₃/w₄ und w₅/w₆ einander gleich, z.B. w₃/w₄ = w₅/w₆ = n und verschiebt dann den Kontakt e, bis das Galvanometer stromlos ist. Dann ist auch X/R = n, also X = R n. War w₃ = w₄ und w₅ = w₆, so kann X = R direkt abgelesen werden.

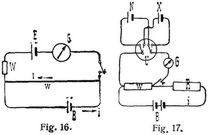
2. Die Messung von Spannungen und Stromstärken geschieht meist direkt durch Spannungs- bezw. Strommesser (s. Meßinstrumente). Für besonders genaue Messungen (Eichungen) oder zur Messung der elektromotorischen Kraft (E.M. K.) von Stromquellen, die bei der Messung stromlos bleiben sollen, bedient man sich der Kompensationsmethoden. – Ein Element E, welches zu einer Stromquelle mit größerer elektromotorischer Kraft (Batterie B) parallel geschaltet ist, kann durch geeignete Wahl der Stromverhältnisse kompensiert, d.h. stromlos gemacht werden, so daß das Galvanometer G keinen Ausschlag gibt (Fig. 16). Dann ist die Spannung iw zwischen den Verzweigungspunkten gleich der elektromotorischen Kraft des[385] kompensierten Elementes, E = iw. Hiernach kann man E finden, wenn man für w einen bekannten Widerstand nimmt und den kompensierenden Strom i mißt. In der Regel mißt man aber eine elektromotorische Kraft durch Vergleichung mit der elektromotorischen Kraft eines Normalelementes, indem man beide nacheinander (mittels Umschalters U) durch ein und dieselbe größere elektromotorische Kraft kompensiert. Dabei läßt man bei beiden Kompensierungen entweder w konstant (Methode Poggendorf) oder i konstant (Methode Du Bois-Reymond). Zum Schutz des Normalelementes und des empfindlichen Galvanometers schaltet man zunächst einen großen Ballastwiderstand W vor, den man bei fast erreichter Kompensierung kurzschließt.

a) Methode Poggendorf (Fig. 17). Hat man bei Kompensierung des Normalelementes N im Rheostaten R_n Ohm, bei Kompensierung des zu messenden Elementes X aber R_x Ohm einschalten müssen, um das Galvanometer auf Null zu bringen, so ist X = (w + R_n/w + R_x)N; w und R sind Widerstandskästen. Damit der Widerstand der Batterie und der Drähte vernachlässigt werden kann, muß w und R genügend groß sein, z.B. w = 1000 Ohm.

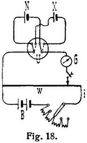
b) Die Methode Du Bois-Reymond läßt sich bequem mit einer Drahtbrücke (s. 1d) ausführen (Fig. 18). Befindet sich nach Kompensierung von N zwischen den Verzweigungspunkten die Drahtlänge l_n, nach Kompensierung von X die Drahtlänge l_n, so ist X = l_n/l_x N.

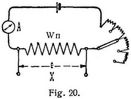
Beide Methoden können auch zu Strommessungen dienen, indem man an Stelle des Elementes X die Spannung an den Klemmen eines Normalwiderstandes kompensiert. Dann ist auch der Strom bekannt, welcher durch diesen Widerstand und durch jeden Apparat fließt, der mit diesem Widerstande hintereinander geschaltet ist (s. Fig. 20).

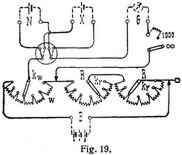
c) Messungen mit dem Kompensationsapparat. Zur bequemen Ausführung aller Kompensationsmethoden hat man alle erforderlichen Widerstande, Umschalter u.s.w. zu einem Apparat vereinigt. Der Widerstand w zwischen den Verzweigungspunkten besteht aus Kurbelrheostaten (Kurbel k_w) und einem Meßdraht mit Schleifkontakt, der Widerstand R ist ein vollständiger Stöpselrheostat oder besteht aus Kurbelrheostaten (Kurbeln k_r). Durch Drehung von k_w ändert sich der Widerstand w zwischen den Verzweigungspunkten, während der Gesamtwiderstand unverändert bleibt (Fig. 19). – Die Messung mit dem Kompensationsapparat ist eine Kombination der Methoden a und b. Man kompensiert zunächst das Normalelement N nach a, indem man bei konstantem w die Kurbeln k_r verstellt, also R ändert. w wählt man dabei so (z.B. w = 10 N), daß nach der Kompensierung i einen bequemen Wert (0,1 Ampère) erhält. Nun kompensiert man nach b) das bei X eingeschaltete Element, indem man k_w verstellt, während R konstant bleibt, also auch i seinen Wert (0,1) behält. Man erhält dann X, indem man den bei k_w abgelesenen Widerstand w_x mit i multipliziert (z.B. X = 0,1 w_x). Hat der Kurbelrheostat w mit dem Schleifdraht zusammen z.B. 110 Ohm, so kann man bei i = 0,l Ampère Spannungen bis 11 Volt messen. Die elektromotorische Kraft der Batterie B muß dann größer als 11 Volt sein. – Diese elektromotorische Kraft bei B kann man auch sofort berechnen, wenn das Normalelement kompensiert, also i = 0,l gemacht ist. Liest man bei den Kurbeln k_r nämlich R Ohm ab, so ist B = 0,1 (110 + R) Volt. Man mißt also Spannungen über 11 Volt, indem man sie bei B einschaltet und durch sie das Normalelement kompensiert (die Klemmen X bleiben dabei frei). Hat man bei R 10000 Ohm zur Verfügung, so kann man Spannungen bis 0,1 (110 + 10000) = 1011 Volt messen.

Soll eine Stromstärke gemessen, z.B. ein Ampèremeter geeicht werden, so schickt man den Strom durch einen Normal widerstand w_n und verbindet dessen Klemmen mit den X-Klemmen des Kompensationsapparates (Fig. 20). Hat man die Spannung e gemessen, so ist die gesuchte Stromstärke J = e/w_n. – Meist arbeitet man mit schwächeren Strömen als 0,1 Ampère, dann wird der Apparat aber teurer, da größere Widerstande erforderlich sind. Ist N = 1,019 Volt (Kadmiumelement) und soll i = 0,001 Ampère sein, so muß w= 1019 Ohm sein, und zur Messung von 1000 Volt sind dann 1000000 Ohm erforderlich.

3. Der Effekt wird am einfachsten mit Hilfe eines Wattmeters (s. Meßinstrumente) gemessen, ein Gleichstromeffekt oder ein Wechselstromeffekt in einem induktionsfreien Leiter auch durch Messung von Strom und Spannung. Besonderer Meßmethoden bedarf es nur, wenn ein Wechselstromeffekt in einem Induktionswiderstand ohne Wattmeter gemessen werden soll (a) oder zur Messung von Drehstromeffekten (b).

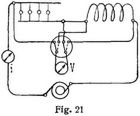
a) Bei Induktionswiderständen genügt wegen der Phasenverschiebung die einfache Strom- und Spannungsmessung nicht zur Bestimmung des Effektes. Man kombiniert dann den Widerstand mit einem induktionsfreien Leiter (z.B. Glühlampen), indem man beide entweder hintereinander oder parallel schaltet. Schaltet man beide hintereinander, so mißt man die Spannung e₁ an den Klemmen des induktionsfreien Widerstandes, die Spannung e₂ an den Klemmen des Induktionswiderstandes, die Gesamtspannung e₀ (Methode der drei Voltmeter) und den[386] gemeinsamen Strom i. Dann ist der Effekt im Induktionswiderstand

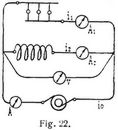
Die drei Spannungen können auch mit einem Voltmeter mittels Umschalter gemessen werden (Fig. 21; bei Kontakt 1 und 4 mißt man e₀). Schaltet man beide Widerstände parallel, so mißt man die beiden Zweigströme i₁, i₂, den Gesamtstrom i₀ (Methode der drei Ampèremeter) und die gemeinsame Spannung e (Fig. 22). Dann ist

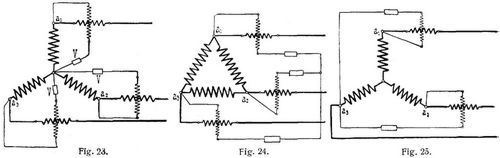
b) Zur Messung des Effektes mehrphasiger Wechselströme sind im allgemeinen mehrere Wattmeter erforderlich. Bei dem üblichen Dreiphasensystem ist am einfachsten die Messung mit drei Wattmetern. Fig. 23 zeigt die Anordnung für Sternschaltung, Fig. 24 für Dreieckschaltung. Ist in ersterem Falle der Nullpunkt nicht zugänglich, so kann man die Spannungsspulen, wie in Fig. 24, zu einem künstlichen Nullpunkt verbinden. Der Gesamteffekt ist gleich der Summe der Wattmeterangaben. E = C₁α₁ + C₂α₂ + C₃α₃. – Die Messung kann auch mit zwei Wattmetern ausgeführt werden, deren Hauptstromspulen in je eine Phase eingeschaltet werden, während die Spannungsspulen zur dritten Phase geführt sind (Fig. 25). E = C₁ α₁ + C₂ α₂. Die Zweiwattmetermethode kann auch mit einem Wattmeter ausgeführt werden, dessen Hauptstromspule mittels eines Umschalters zuerst in Phase I, dann in Phase II gelegt wird, während die Spannungsspule an Phase III liegt. Die beiden α werden hier nacheinander abgelesen. Haben die Ströme sinusförmigen Verlauf und sind die Phasen gleich belastet, so kann nach dieser Methode auch der Phasenverschiebungswinkel α bestimmt werden,

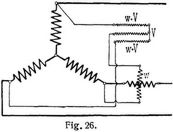
Ist φ > 60°, so wird der eine Ausschlag negativ, das betreffende Wattmeter muß umgeschaltet werden. Das entsprechende α ist dann auch negativ in die Formeln einzusetzen. Bei gleicher Beladung der Phasen kann der Effekt auch mit einem Wattmeter gemessen werden (Fig. 26). Dazu ist ein dreiphasiger Widerstand erforderlich, dessen eine Phase V Ohm, die andern w + V Ohm enthalten, wenn w der Widerstand der Spannungsspule selbst ist.

4. Elektrizitätsmengen, welche während einer längeren, genau meßbaren Zeit fließen, werden mit einem Voltameter (s. Meßinstrumente) gemessen. Sind G mg ausgeschieden worden von einer Substanz, deren elektrochemisches Aequivalent (die von 1 Coulomb ausgeschiedene Menge) gleich α ist, so ist die Elektrizitätsmenge Q = G/a Coulomb.

Elektrizitätsmengen, welche nur sehr kurze Zeit fließen (Kondensatorentladungen, Stromstöße bei Induktionsvorgängen), mißt man mit einem ballistischen Galvanometer, d.h. einem Galvanometer, dessen Magnet eine große Schwingungsdauer besitzt. Fließt die Menge Q in so kurzer Zeit hindurch, daß der Magnet dabei seine Anfangslage noch nicht merklich verlassen hat, daß also die ganze Menge aus der gleichen Entfernung auf die Pole wirkt, dann ist die Menge Q proportional dem Sinus des halben Winkels α, um welchen der Magnet nachträglich, auf Grund des erhaltenen Stoßes, lieh aus der Anfangslage entfernt, also Q = C sin α/2. Meist wendet man Spiegelablesung an und kann dann angenähert sin α/2 = n/4A setzen, wenn die Ablenkung n mm, der Skalenabstand A mm beträgt. Dann ist Q = C_b n, wobei die Konstante C_b = C : 4 A vom Skalenabstande abhängt. Für Spulengalvanometer gilt Q – Cα = Cb n, wobei Cb = C : 2 A ist. Die Konstante C_b bezw. C des Galvanometers bestimmt man durch Eichung; indem man eine bekannte Elektrizitätsmenge Q₀ hindurchschickt und dabei den Ausschlag n₀ bezw. α₀ abliest. Dazu kann man sich eines Erdinduktors bedienen, einer Spule mit großer Fläche F, deren Achse in die Meridianebene eingestellt wird. Der Erdinduktor wird mit dem [387] Galvanometer hintereinander geschaltet und um 180° gedreht. Dadurch wird die Elektrizitätsmenge

erzeugt, wenn H_e die Horizontalkomponente, w der Widerstand des Stromkreises, ξ₀ die Windungszahl ist. Erhält man dabei die Ablenkung n₀, so ist

also

Diese Konstante ist vom Widerstande abhängig, und man kann die Abhängigkeit feststellen, indem man die Bestimmung für verschiedene w ausführt. Für w = ∞ erhält man die Konstante C_b mit Hilfe eines Kondensators. Wird ein Kondensator mit der Kapazität K, der bei einer Spannung E geladen wurde, in das ballistische Galvanometer entladen und dabei die Ablenkung n₀ erhalten, so ist C_b = K E : n₀.

Häufig kommt es bei Induktionsvorgängen nicht auf die Messung von Elektrizitätsmengen, sondern von Kraftlinienzahlen an. Dann kann man die Konstante C_b und den Widerstand mit Hilfe eines Erdinduktors eliminieren. Man kann z.B. die Kraftlinien eines Magnetstabes bestimmen, indem man ihn in eine Spule stößt, die mit einem ballistischen Galvanometer und einem Erdinduktor hintereinander geschaltet ist. Besitzt der Stab θ Kraftlinien, die Spule ξ Windungen, so ist die dabei erzeugte Elektrizitätsmenge (ξθ)/(w10⁸) = C₁ n. Durch Drehung des Erdinduktors erhält man wieder

und durch Division:

woraus θ berechnet werden kann.

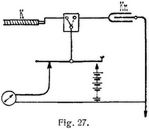
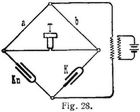
5. Die Kapazität K eines Kondensators kann man mit einem ballistischen Galvanometer messen, dessen Konstante C_b bekannt ist. Hat man den Kondensator durch eine Stromquelle mit der Spannung E geladen und bei der Entladung die Ablenkung n erhalten, so ist K = C_b n : E. Steht ein Wechselstrom von nahezu sinusförmigem Verlauf zur Verfügung, so kann man den Kondensator in den Stromkreis einschalten und die Stromstärke i sowie die Kondensatorspannung e messen. Dann ist K = i : w · e, wenn w = 2 π ~ (~ = Periodenzahl) ist. Diese Methode gibt keine genauen Resultate. Genaue Resultate erhält man durch Vergleichung mit der Kapazität K_n eines Normalkondensators. Das kann dadurch geschehen, daß beide nacheinander durch eine konstante Spannung geladen und in ein ballistisches Galvanometer entladen werden. Gibt der Normalkondensator bei der Entladung einen Ausschlag n₁, der zu messende Kondensator den Ausschlag n, so ist K = n/n₁ K_n. Fig. 27 zeigt die Messung der Kapazität eines Kabels nach dieser Methode. Das Galvanometer kann mit einem passenden Nebenschluß versehen sein. Die Vergleichung kann nach Sauty auch mit der Brückenschaltung ausgeführt werden (Fig. 28), wobei man am einfachsten Wechselstrom (z.B. aus einem Induktionsapparat) verwendet. Hat man die induktionsfreien Widerstände a und b (z.B. Teile eines homogenen Drahtes) so abgeglichen, daß das Telephon schweigt, so ist K = a/b K_n.

6. Bestimmung von Induktionskoeffizienten. Der Selbstinduktionskoeffizient L einer Spule ist nur konstant, wenn sich in der Spule kein Eisen befindet, keine Kapazität vorhanden ist und keine Wirbelströme auftreten. Man kann ihn dann durch Rechnung bestimmen. Ist ξ die Windungszahl, l die Spulenlänge, q deren Querschnitt, so ist L = (4πξ²q)/l C · G · S-Einheiten = (4πξ²q)/(10⁹l) Henry. Schickt man einen Wechselstrom durch die Spule, so kann man L durch Messung der effektiven Stromstärke i und Spannung e bestimmen. Man erhält

wenn w der Ohmsche Widerstand der Spule und ω = 2 π ~ ist. Die Methode ist bequem, die Resultate sind aber nicht sehr genau und um so ungenauer, je mehr die Kurvenform von der Sinuslinie abweicht. Eine genaue Messung erhält man nach Cl. Maxwell durch Vergleichung mit einer Selbstinduktionsnormale mittels der Brückenschaltung. Man schaltet in zwei Zweige der Brücke induktionsfreie Widerstände a und b, in die andern Zweige die zu vergleichenden Selbstinduktionskoeffizienten L_n und L nebst regulierbaren Widerständen und gleicht so ab, daß das Galvanometer sowohl bei Dauerstrom als auch bei Stromimpulsen (beim Ein- und Ausschalten) in Ruhe bleibt. Dann ist L_n : L = a : b = w_n : w, wobei w_n und w die Widerstände in den Induktionszweigen (einschließlich Spulenwiderständen) bedeuten.

Den Koeffizienten M der gegenseitigen Induktion kann man dadurch messen, daß man den Strom i in der primären Spule wendet und dabei mit einem ballistischen Galvanometer die im sekundären Stromkreise erzeugte Elektrizitätsmenge Q mißt. Man erhält

wenn w₂ den Widerstand des sekundären Stromkreises bedeutet. Man kann auch beide Spulen hintereinander schalten, mit gleicher Stromrichtung, und ihren gesamten Selbstinduktionskoeffizienten L_I messen. Sind L₁ und L₂ die Selbstinduktionskoeffizienten der einzelnen Spulen, so ist L_I = L₁ + L₂ + 2M. Nun schaltet man die eine Spule um, so daß der [388] Strom in ihr entgegegengesetzt fließt, und mißt den gesamten Selbstinduktionskoeffizienten L_II. Dann ist L_II = L₁ + L₂ – 2M. Aus beiden Gleichungen folgt M = (L_I – L_II) : 4 [3].

II. Bei den technischen Messungen handelt es sich um die Untersuchung von Materialien (Leitungs- und Isolationsmaterial) und ganzen Anlagen, um Messungen an Maschinen (Gleich- und Wechselstrommaschinen, Transformatoren) sowie an Elementen und Akkumulatoren.

1. Bei Leitungsmaterialien soll der spezifische Widerstand und der Temperaturkoeffizient bestimmt werden. Man hat also den Widerstand w eines Stückes von bestimmter Länge l und bestimmtem Querschnitt q zu messen und hieraus den spezifischen Widerstand c = w q : l zu berechnen. Oder man mißt den Widerstand w₁ bei einer Temperatur T₁ und den Widerstand w₂ desselben Probestückes bei der Temperatur T₂ und berechnet hieraus den Temperaturkoeffizienten

Dazu ist eine der unter I. 1. besprochenen Methoden anzuwenden.

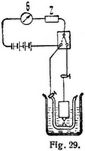
Isolationsmaterialien untersucht man möglichst in Form dünner Scheiben, welche man zwischen zwei Metallplatten preßt oder beiderseits mit Stanniol beklebt. Ein fertiges Kabelstück legt man in ein mit schwacher Lösung gefülltes Gefäß, in das noch eine Metallplatte taucht, und mißt den Widerstand zwischen der Kabelader und der Metallplatte (Fig. 29). Zur Messung großer Widerstände eignet sich am besten die Ersatzmethode (I. 1 a) oder die ihr verwandte Methode des direkten Ausschlages. Die Spannung soll dabei mindestens gleich der Betriebsspannung sein, für welche das Material bestimmt ist. Als Meßinstrument kann ein Drehspulgalvanometer mit Vorschaltwiderstand dienen. Hat man mittels eines Umschalters zuerst X kurz geschlossen und dabei einen Ausschlag α₀ erhalten, während bei eingeschaltetem X sich der Ausschlag α ergibt, so ist

wenn G der Galvanometerwiderstand und z der Zusatzwiderstand ist. Ist X sehr groß, so kann man bei kurzgeschlossenem X eine kleinere Spannung e₀ und bei eingeschaltetem X die ganze Spannung e einschalten. Sind wieder α₀ und α die Ausschläge, so ist

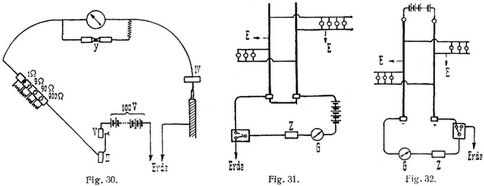
Die Messung kann auch mit dem Universalgalvanometer von Siemens & Halske ausgeführt werden (Fig. 30). Sind die Widerstände 9, 90 und 900 Ω eingeschaltet, so ist G + z = 1000 Ω.

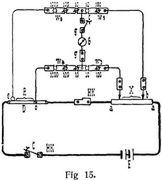
Bei den Isolationsmessungen ganzer Anlagen ist zu unterscheiden, ob die Messungen außerhalb des Betriebes oder während der Betriebszeit auszuführen sind. Im ersten Falle verwendet man eine Hilfsbatterie, deren Spannung der Betriebsspannung gleichkommt. Soll der Isolationswiderstand beider Leitungen gegeneinander gemessen werden, so verbindet man die Batterie nebst Meßinstrument mit den beiden Leitungen und mißt einmal bei kurzgeschlossenem X (beide Leitungen direkt verbunden) und dann bei eingeschaltetem X. Soll der Widerstand des ganzen Netzes gegen Erde gemessen werden, so verbindet man beide Leitungen miteinander und mißt wiederum zuerst bei kurzgeschlossenem X und dann bei eingeschaltetem X, indem man nun das Meßinstrument an Erde (E, z.B. Wasserleitung) legt (Fig. 31). In beiden Fällen ist

Soll die Isolationsmessung während des Betriebes ausgeführt werden, so wird die Betriebsspannung selbst benutzt. Will man zuerst den Isolationswiderstand der positiven Leitung messen, so legt man das Meßinstrument zunächst an beide Leitungen (X kurzgeschlossen), sodann an die negative Leitung und Erde (Fig. 32). Sind α₀ und α₁ die Ausschläge, so ist

Legt man dann das Meßinstrument an die positive Leitung und Erde und findet α₂, so ist

Der Isolationswiderstand der ganzen Anlage ist dann

Besondere Vorrichtungen dienen dazu, das Vorhandensein eines Erdschlusses (Isolationsfehlers) anzuzeigen, und zur Aufsuchung des Fehlerortes (vgl. Isolationswiderstand).

2. Für die Untersuchung von Dynamomaschinen sind von dem Verbände deutscher Elektrotechniker bestimmte Normalien für elektrische Maschinen und Transformatoren aufgestellt worden, und es handelt sich bei der Prüfung von Maschinen darum, festzustellen, wieweit sie diesen Normalien entsprechen. Zu untersuchen sind die Isolationsverhältnisse, das Verhalten der Maschinen[389] bei normaler Belastung sowie bei Ueberlastung, die Temperaturzunahme, die Abhängigkeit der Spannung von der Belastung und der Wirkungsgrad.

Bei Untersuchung des Isolationswiderstandes ist der Isolationswiderstand der Kupferdrähte (Anker- und Magnetwicklung) gegeneinander und gegen das Eisengestell, ferner der des Eisens gegen Erde zu messen. Diese Messungen stimmen im Prinzip mit den ebenbeschriebenen Messungen überein. Das Verhalten der Maschine im Betriebe ist durch einen Dauerversuch von mehreren Stunden zu untersuchen, wobei die Maschine zunächst ungefähr unter normalen Verhältnissen laufen soll. Die Leistung der stromerzeugenden Maschine bestimmt man, indem man sie auf einen passenden Belastungswiderstand (Glühlampen, Flüssigkeitswiderstände u.s.w.) arbeiten läßt und bei verschiedenen Belastungen ihre Leistung mit einem Wattmeter oder mit Strom- und Spannungsmesser mißt. Die Leistung eines Elektromotors mißt man durch ein Bremsdynamometer (s. Dynamometer). Bei beiden Maschinenarten ist zugleich die Tourenzahl festzustellen. Dabei ist auf den Gang der Maschine, die Abnutzung der einzelnen Teile, besonders des Kollektors, auf die Funkenbildung und besonders auf die Erwärmung aller Teile zu achten. Diese bestimmt man durch ein Thermometer oder bei den Kupferdrähten durch Widerstandsmessungen, indem man nach geeigneten Methoden (s. I. 1.) den Widerstand vor Inbetriebsetzung und während des Betriebs mißt. Der Versuch wird fortgesetzt, bis konstante Verhältnisse eingetreten sind. Die Maschine soll auch auf Ueberlastungsfähigkeit untersucht werden, und zwar soll nach den »Normalien u.s.w.« die Maschine für ¹/₂ Stunde eine Ueberlastung von 25% für 3 Minuten eine solche von 40% der normalen Leistung ohne Schaden aushalten.

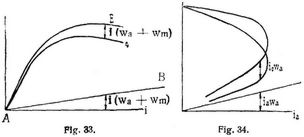
Die Abhängigkeit der Spannung von der Belastung stellt man graphisch dar, die entstehenden Kurven nennt man Charakteristiken. Die Leerlaufscharakteristik (statische Charakteristik) erhält man, indem man die Maschine fremd erregt und für verschiedene Erregungen den Erregerstrom i m und die elektromotorische Kraft der unbelasteten Maschine mißt. Die Tourenzahl soll dabei konstant sein. Gelingt es nicht, sie konstant zu halten, so kann man leicht auf konstante Tourenzahlen reduzieren, da die elektromotorischen Kräfte den Tourenzahlen (bei konstanter Erregung) proportional sind. Die Belastungscharakteristik (dynamische Charakteristik) gibt bei einer belasteten Maschine die Beziehung zwischen dem Ankerstrom und der Klemmenspannung (äußere Charakteristik) oder der elektromotorischen Kraft (innere Charakteristik); die äußere Charakteristik der Nebenschlußmaschine kann auch auf den äußeren Strom i bezogen sein. Die äußere Charakteristik bestimmt man, indem man bei verschiedener Belastung, aber konstanter Tourenzahl, den äußeren Strom und die Klemmenspannung mißt; die innere erhält man durch Rechnung, wenn man den Widerstand des Ankers und der Magnetwicklung gemessen hat. Man trägt die Ströme als Abszissen, die Spannungen als Ordinaten auf. Die Leerlaufscharakteristik aller Maschinen hat die Gestalt einer Magnetisierungskurve und gibt Aufschluß darüber, wie hoch bei der normalen Spannung die magnetische Sättigung des Eisens ist und wie hoch etwa bei dieser Tourenzahl die elektromotorische Kraft noch gesteigert werden kann. Die innere Charakteristik der Serienmaschine hat anfangs auch den Verlauf einer Magnetisierungskurve, bleibt aber wegen der Ankerreaktion immer mehr zurück, erreicht bei einer bestimmten Belastung ein Maximum und nimmt dann wieder ab. Die äußere Charakteristik liegt um den Spannungsverlust i (w_a + w_m), der durch die Gerade A B (Fig. 33) dargestellt wird, tiefer. Die Charakteristik der Nebenschlußmaschine verläuft zunächst horizontal, fällt dann wegen der Ankerreaktion bei gleichzeitig abnehmendem Erregerstrom immer schneller und biegt bei einer maximalen Stromstärke um (Fig. 34). Die Reihenmaschine benutzt man im fallenden Ast der Kurve, oberhalb des Knies, die Nebenschlußmaschine im ersten Teil der Kurve.

Außer der statischen und dynamischen Charakteristik hat, namentlich bei Wechselstrommaschinen, auch die Kurzschlußkurve noch Interesse, welche man erhält, wenn man bei fremder Erregung den Anker durch einen Strommesser kurz schließt und die Erregung allmählich steigert, bis der höchstzulässige Ankerstrom erreicht ist. Man kann sich auch aus der Leerlaufs- und der Kurzschlußcharakteristik ein Urteil bilden über das Verhalten der Maschine bei normaler Belastung. Vgl. [1].

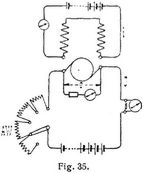
Der Wirkungsgrad oder das Güteverhältnis einer Dynamomaschine kann entweder nur mit Berücksichtigung der elektrischen oder der gesamten Verluste bestimmt werden. Im ersten Falle erhält man das elektrische Güteverhältnis η, im letzten Falle das totale Güteverhältnis η'. Es ist also bei einer stromerzeugenden Maschine η = Nutzeffekt: (Nutzeffekt + elektrischer Verlust), η' = Nutzeffekt: (Nutzeffekt + gesamter Verlust), bei einem Motor η = (Gesamteffekt – elektrischer Verlust): Gesamteffekt und η' = (Gesamteffekt – gesamter Verlust): Gesamteffekt. Die elektrischen Güteverhältnisse bestimmt man, indem man mit Strom- und Spannungsmesser den Nutzeffekt (beim Generator) bezw. den Gesamteffekt (beim Motor) mißt und aus den Widerständen die Verluste berechnet. Das totale Güteverhältnis η' eines Motors bestimmt man, indem man seine Nutzleistung durch Bremsung feststellt und durch den gemessenen Gesamteffekt e i dividiert. Zur Messung der Nutzleistung kann man statt eines Dynamometers (s.d.) auch eine Wirbelstrombremse verwenden. Durch den Motor wird eine Kupferscheibe gedreht, welche sich an den Polen eines kräftigen Elektromagneten vorbeibewegt. Dadurch werden [390] Wirbelströme erzeugt, welche die Scheibe festzuhalten oder den auf Schneiden gelagerten und ausbalancierten Elektromagneten mitzunehmen suchen. Das auf diesen ausgeübte Drehmoment wird dadurch gemessen, daß ein Gewicht P auf einem Hebelarm bis zu einem Abstand R verschoben wird, für welchen sich der Magnet im Gleichgewicht befindet. Multipliziert man das Drehmoment P R mit 2 π n_B : 60, wenn n_B die Umdrehungszahl der Scheibe ist, so erhält man den Nutzeffekt E_n des Motors; in Watt ist E_n = 9,81 · 2 π n_B · P R : 60 = 1,03 n_B P R, also η' = 1,03 n_B P R : e i. Um η' für einen Generator zu erhalten, muß man die gesamten Verluste bestimmen, wozu außer den elektrischen Verlusten noch die sogenannte Leerlaufsarbeit E_v gehört, nämlich die Effektverluste durch Reibung (E_R), durch Hysteresis (E_H) und durch Wirbelströme (E_W). Man bestimmt E_v durch Versuche, indem man die Maschine unbelastet als Motor mit fremder Erregung laufen läßt und den Ankerstrom J sowie die Klemmenspannung e, ferner den Erregerstrom i und die Tourenzahl n mißt (Fig. 35). Zieht man von e J den Effektverlust im Anker J² w_a ab, so erhält man E J, und das ist die Leerlaufsarbeit E. Diese Messung führt man bei konstanter Erregung für verschiedene Ströme J aus (mittels veränderlichen Anlaßwiderstandes A W) und kann dann eine Kurve konstruieren, indem man die Tourenzahlen als Abszissen und die E_v als Ordinaten aufträgt. Bestimmt man mehrere solche Leerlaufskurven für verschiedene Erregungen, so kann man daraus für jede beliebige Tourenzahl und jede Erregung die Leerlaufsarbeit E_v entnehmen. Das Güteverhältnis ist dann, wenn E der gemessene Nutzeffekt der Maschine, E_a der Effektverlust im Anker, E_m der im Magneten ist, η' = E: (E + E_a + E_m + E_v). Häufig ist es von Interesse, die Verluste zu trennen, also E_v in die Bestandteile zu zerlegen, wenn man z.B. ein mangelhaftes Güteverhältnis verbessern möchte. Man kann dann aus den Leerlaufskurven neue Kurven ableiten, die für eine bestimmte Tourenzahl die Leerlaufsarbeit als Funktion der Erregung darstellen. Man erhält z.B. die Kurve für die Tourenzahl n₁ indem man bei n₂ die Ordinaten aller Leerlaufskurven abmißt und als Ordinaten zu den entsprechenden Erregerströmen aufträgt. Verlängert man alle Kurven der zweiten Schar bis zur Ordinatenachse, so geben die Schnittpunkte die Leerlaufsarbeiten bei der Erregung 0 an, d.h. die Reibungsverluste. Damit ist eine Kurve für die Reibung als Funktion der Tourenzahl gegeben. Zieht man von den ersten Kurven die Reibungsverluste ab, so erhält man Kurven für (E_H + E_W). Will man auch diese trennen, so beachte man, daß E_H proportional n, E_W aber proportional n₂ ist, daß man also (E_H + E_W) = a_Hn + a_Wn² setzen kann. Entnimmt man nun aus den Kurven für (E_H + E_W) zwei Wertepaare und setzt sie in die Gleichung ein, so kann man a_H und a_W berechnen und damit E_H und E_W einzeln bestimmen. Man kann die Trennung auch durch weitere Konstruktion von Kurven ausführen. Ausführliches darüber sowie über die zusätzlichen Eisenverluste, die man den so gefundenen Verlusten hinzufügen muß, um die Verluste für eine belastete Maschine zu erhalten, s. [1], [2].

Für die Berechnung von Dynamomaschinen ist die Kenntnis des Streuungskoeffizienten υ der verschiedenen Typen erforderlich. Man versteht darunter das Verhältnis der im Magnetgestell erzeugten Kraftlinienzahl N_m zu der im Anker nutzbar gemachten Kraftlinienzahl N₀, also υ = θ_m/θ₀. Man kann dieses Verhältnis mit einem ballistischen Galvanometer bestimmen, indem man um einen Magnetschenkel (nahe am Joch) und um den Anker Hilfsspulen von gleicher Windungszahl legt; die letztere muß mitten vor der Polfläche liegen und die Breite der Polteilung besitzen, z.B. bei einer vierpoligen Maschine ein Viertel des Ankerumfanges umfassen. Die Maschine wird dabei in normaler Weise erregt. Aendert man nun die Erregung, z.B. durch Schwächen oder Wenden des Stromes, so werden in den Spulen Elektrizitätsmengen induziert, welche in dem ballistischen Galvanometer Ausschläge bewirken. Das Verhältnis der Ausschläge gibt den Streuungskoeffizienten υ.

Bei der Untersuchung von Elementen oder Akkumulatoren ist der innere Widerstand zu messen (I. 1.), der bei Akkumulatoren auch aus den Dimensionen und dem spezifischen Widerstand der Säure (ca. 1,4 Ohm für 1 ccm) berechnet werden kann. Bei primären Elementen mißt man nach (I. 2.) die elektromotorische Kraft des unbelasteten Elementes und untersucht dann, wie das Element bei verschiedenen Belastungen abnimmt und nach wie viel Amperestunden es erschöpft ist. Bei Akkumulatoren genügt es meist, die Spannung mit einem Voltmeter zu messen, und zwar für jede Zelle und die ganze Batterie. Dann nimmt man eine Ladung und Entladung mit normaler Stromstärke vor und bestimmt die Lade- und Entladekurve (vgl. Akkumulatoren). Dabei kann man auch die aufgenommene und abgegebene Elektrizitätsmenge resp. Energie bestimmen. Ist der Akkumulator in T₁ Stunden mit dem Strom J₁ geladen worden, so hat er J₁ T₁ Coulomb aufgenommen; hat er bei der Entladung T₂ Stunden J₂ Ampère gegeben, so ist seine Kapazität in Amperestunden K = J₂T₂ und sein Güteverhältnis in Amperestunden η = J₂T₂/J₁T₁. War J nicht konstant, so muß man in bestimmten Intervallen messen und die Σ J T bilden. Ebenso muß man auch verfahren, wenn man die elektrische Energie messen will. Man bestimmt dann die Σ e J T für die Ladung und für die Entladung (letztere ist die Kapazität in Wattstunden); das Verhältnis beider ist das Güteverhältnis η' in Wattstunden.

B. Magnetische Messungen.

Es soll hier nur die Messung derjenigen magnetischen Größen (s. Magnetismus) besprochen werden, welche in der Elektrotechnik eine besondere Rolle spielen (s. Elektromagnetismus).[391] Bei den Konstruktionen von Dynamomaschinen muß das magnetische Verhalten der dabei verwendeten Eisensorten bekannt sein. Man bestimmt das Verhalten des Eisens bei der Magnetisierung, indem man für verschiedene Werte der magnetisierenden Kraft H den jedesmaligen Grad der Magnetisierung, die magnetische Induktion B bestimmt. Stellt man die Beziehung zwischen H und B graphisch dar, so erhält man die Magnetisierungskurve des Eisens. Für das Güteverhältnis der Maschinen kommt die Beschaffenheit des Eisens auch noch insofern in Betracht, als bei fortgesetzten Ummagnetisierungen ein Effektverbrauch durch Hysteresis verursacht wird. In einigen praktischen Fällen (elektrische Bremsvorrichtung) spielt auch die Tragkraft oder Anziehungskraft der Magnete oder Elektromagnete eine Rolle.

1. Bestimmung der Magnetisierungskurve. Man magnetisiert ein Probestück aus dem zu untersuchenden Material durch eine Spule und bestimmt für verschiedene Grade der Magnetisierung H und B. H ergibt sich aus der Stromstärke und der Windungszahl und ist H = 0,4 π z i : l, wobei l die Länge der mittleren Kraftlinie ist. Zur Bestimmung des jedesmaligen B gibt es verschiedene Methoden:

a) Mit dem Magnetometer. Die Magnetisierungsspule wird mit dem Eisenstabe in die Ostwestrichtung gebracht, in die Verlängerung ihrer Achse eine Magnetnadel, welche unter dem Einfluß des magnetisierten Stabes um einen Winkel α abgelenkt wird. Dann ist die Intensität der Magnetisierung

wobei r den Abstand der Nadel von der Stabmitte, L die Stablänge, q den Querschnitt der Spule bedeuten. Bei Spiegelablesung kann man tg α = n : 2 A setzen und erhält

Hat man durch Messung des Stromes i auch H = 0,4 π z i : l bestimmt, so ist die Induktion B = H + 4 π J. Da man den magnetischen Widerstand des Eisens vernachlässigt, setzt man für L die Spulenlänge. Das ist aber nur zulässig, wenn der Stab sehr lang ist im Verhältnis zu seinem Durchmesser (mindestens das 300 fache). – Will man den Einfluß, welchen die Magnetisierungsspule selbst auf die Magnetnadel ausübt, beseitigen, so bringt man auf der andern Seite eine Kompensationsspule an, die man vor dem Eindecken des Magnetstabes so einstellt, daß für irgend einen Strom die Nadel auf Null bleibt. – Nach dieser Methode kann man auch die gesamte Hysteresisschleife bestimmen, indem man den Strom allmählich steigert, wieder abnehmen läßt, mit entgegengesetzter Richtung steigert und wieder abnehmen läßt.

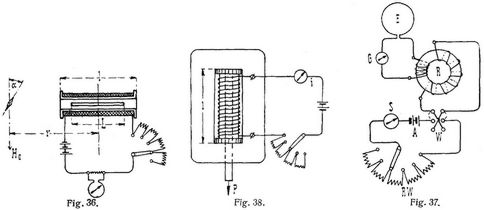
b) Mit dem ballistischen Galvanometer. Unter A.I. 4 war zum Schluß als Beispiel für Messungen mit dem ballistischen Galvanometer die Bestimmung der Kraftlinienzahl θ eines Magnetstabes gegeben worden. Die Messung ließe sich für einen Elektromagneten ausführen, den man samt der Magnetisierungsspule in die Induktionsspule steckt. Um aber die Schwierigkeit der Bestimmung des l zu umgehen, fertigt man aus der zu untersuchenden Eisensorte einen Ring an, auf welchem man die Magnetisierungsspule mit z und die Induktionsspule mit ξ Windungen anbringt (Fig. 37). Da man den Ring nicht in die Spule stoßen oder herausziehen kann, so wendet man den Strom, so daß sich die Kraftlinienzahl von + θ auf – θ, also um 2 θ ändert.

Die dort abgeleitete Formel heißt dann

woraus

n folgt. Ist q der Querschnitt des Ringes, so ist die Induktion

In der Formel H = 0,4 π z i : l ist für l der mittlere Umfang des Ringes zu setzen.

c) Messung mit dem Durchlässigkeitsmesser (Permeameter). Die Kraft, mit welcher ein Elektromagnet einen Anker anzieht oder festhält, ist P = B² q : 8 π · 981000 kg. Mißt man die Kraft P durch Abreißen des Ankers, so kann man daraus B berechnen. Man erhält

(bezw.

bei einem Hufeisenmagneten). Zur genauen Messung der Kraft P und zur genauen Bestimmung von l hat Silv. Thompson den in Fig. 38 dargestellten Apparat konstruiert. Der Probestab wird durch den Eisenrahmen in die Magnetisierungsspule gesteckt, so daß er an der inneren Rahmenwandung anliegt und hier angezogen wird. Man spannt nun eine Federwage, bis der Stab abreißt, und liest auf der Skala die Kraft P, an einem eingeschalteten Strommesser den Strom i ab. Will man den Einfluß der Spule selbst berücksichtigen, so setzt man

wobei q den Querschnitt des Stabes bedeutet.[392] In der Formel H= 0,4 π z i : l ist für l der Abstand der beiden inneren Rahmenflächen zu setzen, da der magnetische Widerstand des Rahmens vernachlässigt werden kann. Auf der Messung der magnetischen Zugkraft des magnetisierten Eisens beruht auch die Präzisionswage von Du Bois, bei welcher ein Laufgewicht auf einem Wagebalken zur Messung dient [2]–[4].

2. Zur Messung der Intensität magnetischer Felder kann die Eigenschaft des Wismuts verwendet werden, da es in einem magnetischen Felde seinen Leitungswiderstand ändert. Ein dünner Wismutdraht ist zu einer flachen Spirale bifilar aufgewickelt, so daß sie z.B. zwischen Anker und Magnet einer Dynamomaschine gebracht werden kann. Die Widerstandsänderung gibt ein Maß für die Kraftlinienzahl pro Quadratzentimeter, und es entsprechen 1000 Kraftlinien etwa 5% Widerstandsänderung. Aus einer Eichkurve kann zu jeder Widerstandsänderung die Kraftliniendichte abgelesen werden.

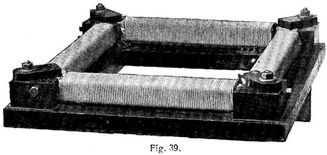
3. Für die Untersuchung von Eisenblechen in bezug auf Hysteresisverluste hat der Verband deutscher Elektrotechniker bestimmte Normalien aufgestellt und als »Verlustziffer« des Eisens den Wattverbrauch pro 1 kg für B_max = 10000 und 50 Perioden bei 30° festgesetzt. Zur Ausführung der Messungen dient u.a. der Apparat von Epstein (Fig. 39). Das zu untersuchende Blech wird hierzu in Streifen geschnitten, die mit Seidenpapier voneinander isoliert und mit Isolierband zu vier festen Paketen vereinigt werden. Die Pakete werden in vier Magnetisierungsspulen geschoben und zu einem Viereck zusammengelegt und dann durch Spannvorrichtungen fest aneinander gepreßt. Durch die Spulen schickt man einen Wechselstrom von 50 Perioden, den man so einreguliert, daß B_max = 10000 wird. Nun mißt man mit einem Wattmeter den Effekt E und gleichzeitig die Stromstärke i und die Spannung e. Dann ist der reine Eisenverlust =

wenn W der Widerstand der Magnetisierungsspulen, w₁ der des Voltmeters und w₂ der der Spannungsspule des Wattmeters ist.

4. Die Zugkraft oder Tragkraft der Elektromagnete kann man durch einfache Belastung bestimmen. Zur Feststellung der Zugkraft bringt man den Anker des vertikal gestellten Elektromagneten in verschiedene Entfernungen vom Pol und stellt für verschiedene Beladungen denjenigen Strom fest, welcher den Anker anzieht. Zur Untersuchung der Tragkraft belastet man bei verschiedenen Stromstärken den Anker, bis er abreißt.

Literatur: [1] Handbuch der Elektrotechnik, Bd. 2, Leipzig 1905. – [2] Holzt, Schule des Elektrotechnikers, Leipzig 1907. – [3] Strecker, Hilfsbuch für die Elektrotechnik, Berlin 1906. – [4] Niethammer, Elektrotechnisches Praktikum, Stuttgart 1902.

Holzt.

Fig. 1.

Fig. 2., Fig. 5.

Fig. 3.

Fig. 4., Fig. 6.

Fig. 7.

Fig. 8.

Fig. 9., Fig. 10., Fig. 11.

Fig. 12., Fig. 13., Fig. 14.

Fig. 15.

Fig. 16., Fig. 17.

Fig. 18.

Fig. 19.

Fig. 20.

Fig. 21.

Fig. 22.

Fig. 23., Fig. 24., Fig. 25.

Fig. 26.

Fig. 27.

Fig. 28.

Fig. 29.

Fig. 30., Fig. 31., Fig. 32.

Fig. 33., Fig. 34.

Fig. 35.

Fig. 36., Fig. 37., Fig. 38.

Fig. 39.