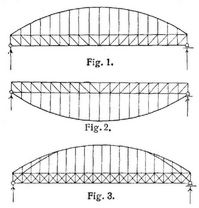
Bogensehnenträger

Bogensehnenträger hat man mitunter Träger genannt, die aus einem Balken (s.d.) und einem durch Tragstangen damit verbundenen Bogen (s.d.) aus axial beanspruchten Stäben bestehen (Fig. 1 und 2). Der aus Balken und Bogen zusammengesetzte Träger erhält ein festes und ein horizontal verschiebbares Gelenkauflager, so daß bei beliebiger (vertikaler) Belastung nur vertikale Drücke auf die Stützen entstehen, was für die Stabilität der letzteren und die Beanspruchung des Fundamentbodens günstig ist. Während hiernach der Träger im ganzen als Balken angesehen werden kann, gelangen die Stützpunkte der Zwischenträger in geringere Entfernungen als bei gewöhnlichen Balken von gleicher Höhe und einfachem Fachwerksystem. Bei untenliegender Fahrbahn kann gewöhnlichen Balkenfachwerken gegenüber auch in Betracht kommen, daß der Querverkehr und die Aussicht nicht durch schiefe Stäbe gestört werden (vgl. Bogen mit Zugstange). Beispiele der Ausführung solcher Träger bilden die Mühlbrunnbrücke in Karlsbad (Bogen oben, gekreuzte Diagonalen), die Adlerbrücke in Senftenberg (Bogen unten, gekreuzte Diagonalen), die Ihmbrücke in Hannover (Bogen oben, System des gleichschenkligen Dreiecks) und andre.

Für die Berechnung obiger Träger gelten die unter Fachwerke, statisch unbestimmte, gegebenen Beziehungen, die je nach Umständen noch spezialisiert werden können [7]. Bei vollwandigem Balken wäre nach den Gleichungen unter Kombinierte Träger oder weiter vorbereiteten Formeln zu rechnen [6]. Ist der Balken vollwandig oder ist die Stabanordnung des Balkenfachwerks derart, daß der Balken ohne den Bogen statisch bestimmt wäre, dann wird der aus beiden zusammengesetzte Träger einfach statisch unbestimmt, man hat nur eine Größe aus Elastizitätsgleichungen zu berechnen, als welche die Beanspruchung irgend eines Bogenstabs oder bei nur vertikalen Aktivkräften (Lasten) die Horizontalkomponente der Beanspruchungen aller Bogenstäbe gewählt werden kann. Durch Einschaltung eines Zwischengelenks im Balken könnte in solchen Fällen ein statisch bestimmter Träger hergestellt werden (vgl. Mittengelenkbalken). Bei der Ferdinandsbrücke in Graz spaltet sich der Bogen in der Nähe der Auflager (Fig. 3), was selbstverständlich bei der Berechnung zu berücksichtigen ist [3]–, [4].

Literatur: [1] Festigkeitstheorie der Brückenträger nach Langers System, Techn. Blätter 1871, S,34, 165. – [2] Hoech, Versteifte Bogensehnenträger, Civilingenieur 1882, S. 165. – [3] Brik, Die Ferdinandsbrücke in Graz, Zeitschr. d. österr. Ing.- u. Arch.-Vereins 1883, S. 43. – [4] Müller-Breslau, Beiträge zur Theorie der Versteifung labiler und flexibler Bogenträger, Zeitschr. f. Bauwesen 1883, S. 312. – [5] Ders., Beitrag zur Theorie des durch einen Balken versteiften Bogens, Zeitschr. f. Bauwesen 1884, S. 323. – [6] Winkler, Theorie der Brücken, 1. Heft, Wien 1886, S. 185. – [7] Müller-Breslau, Die graphische Statik der Baukonstruktionen, II, Leipzig 1903, S. 243.

Weyrauch.

Fig. 1., Fig. 2., Fig. 3.