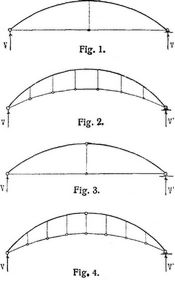
- Bogen mit Zugstange
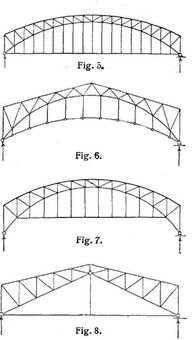
Bogen mit Zugstange sind Bogenträger mit Endgelenken (s. Bogen, einfache, und Bogenfachwerke), deren Horizontalschub durch eine axial beanspruchte Zugstange anstatt durch die Widerlager aufgenommen wird. Der aus Bogen und Zugstange zusammengesetzte Träger erhält ein festes und ein horizontal verschiebbares Gelenkauflager, so daß bei beliebiger (vertikaler) Belastung nur vertikale Drücke auf die Stützen kommen (der Träger also als Balken angesehen werden kann), was für die Stabilität der Stützen und die Beanspruchung des Fundamentbodens günstig ist. Da jedoch der gleiche Zweck auch durch gewöhnliche Balkenträger, z.B. durch Balkenfachwerke von Segmentform oder Sichelform erreicht werden kann, so pflegen noch ästhetische, konstruktive oder sonstige Gesichtspunkte für die Anwendung solcher Träger in Betracht zu kommen. Bei Brücken mit untenliegender Fahrbahn beispielsweise sollte eine Durchschneidung der Landschaft durch schiefe Füllungsglieder und mitunter eine Störung des Querverkehrs vermieden werden, auch wollte man mehrfach die Unterstützungen der Zwischenträger einander näher bringen (vgl. Bogensehnenträger und Mittengelenkbalken). Die Zugstange verbindet gewöhnlich die Endgelenke, doch ist dies nicht unbedingt nötig, wie z.B. Fig. 7 der Eisenbahnbrücke über den Rhein bei Worms entspricht [7].
Die Stützenreaktionen V,V' des ganzen Trägers ergeben sich ganz wie für gewöhnliche Balken (s. Balken, einfache). Für die weitere Berechnung ist vor allem der Horizontalschub H auszudrücken. Dies soll im folgenden für die gewöhnlichsten Fälle horizontaler Zugstange in Höhe der Endgelenke von konstantem Querschnitt F' und gleichem Material wie der Bogen geschehen, wonach die Berechnung des letzteren unter Verwendung dieses Horizontalschubs (und der entsprechenden Kämpferdrucklinie) ganz wie für Zweigelenkbogen ohne Zugstange erfolgen kann (s. Bogen, einfache, und Bogenfachwerke). Für andre Fälle kommen die unter Fachwerke, statisch unbestimmte, und Kombinierte Träger gegebenen Beziehungen zur Verwendung. Vorausgesetzt wird, daß keine Verkürzung der Spannweite des Bogens durch Einsenken der Zugstange in Betracht kommt, was man durch Aufhängen der letzteren in der Mitte oder an mehreren Stellen zu erreichen sucht (Fig. 1 und 2).
Vollwandige Bogen.
Werden die für Bogen mit zwei Gelenken unter Bogen, einfache verwendeten Bezeichnungen beibehalten und zur Abkürzung gesetzt:
dann erhält man für symmetrische Parabelbogen von konstantem (mittlerem) J cos φ (gleich c) durch beliebige Belastung:
durch beliebige gleichmäßige Temperaturänderungen τ des Bogens und τ' der Zugstange:
also speziell
[175] Im Falle gleichmäßig verteilter Last von u pro Längeneinheit Träger auf der ganzen Spannweite nimmt 2. die Form an (vgl. Belastung der Träger):
Nach 1. nähert sich h um so mehr dem für Zweigelenkbogen ohne Zugstange geltenden Werte (1 + ε)8 f2, je größer der Querschnitt F' der Zugstange ist, für F' = ∞ würde jener Wert von h und damit derselbe Horizontalschub H durch Belastung wie beim gewöhnlichen Zweigelenkbogen erreicht. Bei Berechnung des Querschnitts F' kann man dies etwas zu ungünstige H verwenden. Daß für die bei Brücken und Dächern vorkommenden Bogen β immer vernachlässigt und bei vorläufigen Berechnungen meist ε = 0 sowie je nach Umständen in 2. anstatt l2 + la – a2 sein Mittelwert (7/6)l2 gesetzt werden kann, bedarf nach dem für gewöhnliche Zweigelenkbogen Gesagten (s. Bogen, einfache) keiner Erwähnung. Die Gleichung der Kämpferdrucklinie ist bei Vernachlässigung von β:
Ueber Dreigelenkbogen mit Zugstange (Fig. 4) s. unten.
Es gelten die unter Fachwerke, statisch unbestimmte, gegebenen Beziehungen. Im folgenden setzen wir voraus, daß der Träger ohne die Zugstange statisch bestimmt wäre, wie beispielsweise im Falle der Fig. 5. Die Elastizitätsmoduln E und Ausdehnungskoeffizienten α seien für alle Stäbe gleichgroß. Ferner mögen wie bei gewöhnlichen Zweigelenkbogenfachwerken für einen beliebigen Bogenstab bezeichnen s die Länge, F den Querschnitt, π die Beanspruchung durch einen Horizontalschub H = 1 allein und A die Beanspruchung, die für die in Frage kommende Belastung im Falle H = 0 (bei Wegfall der Zugstange) entstehen würde. Dann hat man mit der Bezeichnung
durch beliebige Belastung:
durch beliebige gleichmäßige Temperaturänderungen τ des Bogens und τ' der Zugstange:
und speziell
In 7. und 8. beziehen sich die Summen Σ auf alle Bogenstäbe. Nachdem der Horizontalschub H (die Beanspruchung der Zugstange) bekannt ist, hat man die ganze Beanspruchung eines beliebigen Bogenstabes für die in Frage stehende Belastung (der bei fehlender Zugstange die Beanspruchung A dieses Stabes entsprechen würde):
Bei Ermittlung des Beitrags von τ, τ' ist A = 0. Die Gleichung der Kämpferdrucklinie ist wie bei gewöhnlichen Zweigelenkbogenfachwerken (a Abszisse, b Ordinate):
worin der Horizontalschub H einer bei a angreifenden Einzellast P = 1 entspricht. In bezug auf die Ermittlung der Stabkräfte S bleibt es bei dem für gewöhnliche Zweigelenkbogenfachwerke Gesagten (s. Bogenfachwerke).
Wird innerhalb des Bogens ein Gelenk angeordnet (Fig. 4 und 8), so ist der Horizontalschub H statisch bestimmt. Bei horizontaler Zugstange kann die Berechnung von H und sämtlicher Schnittkräfte oder Stabkräfte ganz wie für gewöhnliche Dreigelenkbogen erfolgen (s. Bogen, einfache, und Bogenfachwerke). Da mit H bei horizontaler und gesprengter Zugstange auch die Beanspruchungen der letzteren bestimmt sind, so ergibt sich der Querschnitt der Zugstange nun ohne Rücksicht auf die Formänderungen.
Literatur: [1] Castigliano, Théorie de l'équilibre des systèmes élastiques, Turin 1880, p.352 (deutsche Ausgabe Wien 1886, S. 354). – [2] Brik, Zur Berechnung eines besonderen Konstruktionssystems bogenförmiger Dachbinder, Zeitschr. d. österr. Ing.- u. Arch.-Vereins 1882, S. 100. – [3] Landsberg, Berechnung frei tragender Wellblechdächer, Zeitschr. f. Bauwesen 1891, S. 387. – [4] Walbaum, Die Leobener Murbrücke im Zuge der Italiener Reichsstraße, Allgem. Bauztg. 1897, S. 136. – [5] Weyrauch, Elastische Bogenträger u.s.w., München 1897, S. 157. – [6] Haberkalt, Der Neubau der Johannesbrücke in Ischl, Allgem. Bauztg. 1899, S. 21. – [7] Geibel, Die Eisenbahnbrücke über den Rhein bei Worms, Zeitschr. d. Vereines deutscher Ingenieure 1900, S. 1629. – [8] Müller-Breslau, Die graphische Statik der Baukonstruktionen, II, Leipzig 1903, S. 243.
Weyrauch.
http://www.zeno.org/Lueger-1904.