Lastäquivalente

Lastäquivalente, Lastgleichwerte oder Belastungsäquivalente, Belastungsgleichwerte, nennt man in der Ingenieurmechanik diejenigen gleichmäßig verteilten Verkehrslasten pro Längeneinheit der verkehrsbelasteten Strecke eines Trägers oder auch pro Quadratmeter Brückenbahn (Straßenbrücken), welche gleiche Beanspruchungen B (Momente, Vertikalkräfte, Stabkräfte u.s.w.) wie die wirklichen Lasten (Lokomotiven, Bahnzüge, Fuhrwerke u.s.w.) ergeben. Häufig werden solche Lastäquivalente p an Stelle konzentrierter Lasten bei Bestimmung der Grenzwerte (s.d.) von B verwendet, da hiermit die Annahmen leichter vergleichbar und die Berechnungen einfacher als bei Zügen mit verschiedenen konzentrierten Lasten und Radständen sind. Doch setzt dies voraus, daß man die maßgebenden gleichmäßig verteilten Lasten kennt oder die verwendeten p jedenfalls keine günstigeren Beanspruchungen als die wirklichen Verkehrslasten liefern (vgl. Dimensionenberechnung, Grenzwerte). Es zeigt sich, daß die einem gegebenen Lastzüge entsprechenden p auch bei einem bestimmten [71] Träger für verschiedene Größen B und selbst für die beiden Grenzwerte einer bestimmten Größe B verschieden ausfallen können [2], [10] Beispiele 7, 8, 29 u.s.w.

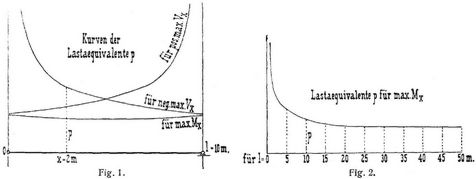
Für einen durch Lokomotiven befahrenen gewöhnlichen Balkenträger (Bd. 1, S. 519) beispielsweise lassen sich zwar die größten Angriffsmomente M_x in allen Querschnitten x genügend genau mit dem gleichen Werte p berechnen, nicht aber die Grenzwerte der Vertikalkräfte V_x. In Fig. 1 sind für einen solchen Träger die in einem Beispiele [10] B 7 berechneten p als Ordinaten bei ihren Querschnitten x aufgetragen. – Die p für die M_x nehmen von den kleinsten Spannweiten l an mit wachsendem l zunächst verhältnismäßig rasch ab und nähern sich dann asymptotisch einem festen Werte, wie dies in Fig. 2 einem Beispiele [10] B 8 entsprechend angedeutet ist. Für die V_x gilt der Satz: Bei bestimmtem Lastzug sind für gewöhnliche Balkenträger aller Spannweiten l die Lastäquivalente p zur Berechnung der pos max V_x in allen Querschnitten von gleichen l – x gleich groß, und ebenso die p zur Berechnung der neg max V_x in Querschnitten von gleichen x. Beispielsweise entspricht der größten Stützenreaktion bei 0 (= pos max V_x für x = 0, s. Bd. 1, S. 522) eines Trägers der Spannweite l dasselbe p wie dem pos max V_x in demjenigen x eines Trägers der Spannweite L, für welchen L – x = l ist, [4], [10], S. 37. – Ueber Werte der p in wichtigen Fällen gibt die unten angeführte Literatur Aufschluß. Ausdrücke der p als Funktion der Spannweite l und sonstiger Verhältnisse s. [8], [9], [12]. Zu beachten ist, daß mit Zunahme der Gewichte der Fahrzeuge (Lokomotiven, Straßenwalzen u.s.w.) auch die äquivalenten p gewachsen sind.

Literatur. [1] Heinzerling, Belastungsäquivalente zur Bestimmung der durch fortschreitende Eisenbahnzüge erzeugten größten Vertikalscherkräfte in Brückenträgern von 10–150 m Stützweite, Zeitschr. f. Bauwesen 1875, S. 509. – [2] Fränkel, Ueber die ungünstigste Belastung von Bogenträgern mit zwei Gelenken, Civilingenieur 1875, S. 585. – [3] Laißle und Schübler, Der Bau der Brückenträger, I, Stuttgart 1876, S. 114, 127. – [4] Schäffer, Vergleich der Brückenbelastungen durch Lokomotivzüge mit gleichförmig verteilten Belastungen, Deutsche Bauztg. 1876, S. 348. – [5] Kleitz, Note sur la substitution dans les calculs de stabilité de travées métalliques supportants de voies de terres, de surcharges uniformément reparties à celles qui résultent du passage des plus lourdes voitures, Annales des ponts et chaussées 1877, II, S. 549. – [6] Engesser, Belastungsäquivalente bei Eisenbahnbogenbrücken, Deutsche Bauztg. 1879, S. 322. – [7] Landsberg, Stellvertretende gleichmäßig verteilte Belastung für die Ermittelung der Querkräfte bei Brücken, Zentralbl. der Bauverwalt. 1883, S. 190. – [8] Winkler, Ueber die Belastungsgleichwerte der Brückenträger, Festschrift der Technischen Hochschule zu Berlin, 1884, S. 83 (Auszug: Zentralbl. d. Bauverwalt. 1884, S. 460, 465). – [9] Ders., Theorie der Brücken, 1. Heft, Wien 1886, S. 326. – [10] Weyrauch, Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888 (Aufgaben 11, 29, 30, 32, 34, 35, 36, 37, 48 und die am Schlusse von Aufg. 29 erwähnten Beispiele); Theorie der statisch bestimmten Träger u.s.w., Leipzig 1887, S. 38, 90. – [11] Collignon, Note sur la determination des limites de l'effort tranchant dans les poutres droites, Annales des ponts et chaussées 1889, XVII, S. 125, und XVIII, S. 331. – [12] Seefehlner, Beiträge zu den bei eisernen Balkenbrücken vorkommenden Berechnungen, Allgem. Bauztg. 1893, S. 51. – [13] Hoffmann, Bestimmung der Belastungsgleichwerte für gerade Straßenbrücken, Zeitschr, s. Bauwesen 1893, S. 331. – [14] Engesser, Was für Verkehrsbelastungen sind der Berechnung eiserner Bahnbrücken zugrunde zu legen? Deutsche Bauztg. 1894, S. 141. – [15] Collignon, Note sur la méthode des deux surcharges continues pour le calcul des ponts métalliques à poutres droites, Annales des ponts et chaussées 1895, II, S. 5. – [16] Hauger, Belastung und Berechnung eiserner Brücken, Allgem. Bauztg. 1896, S. 111. – [17] Johnson, Modern framed structures, 1897, S. 101. – [18] Podhajsky, Beitrag zur Lehre von den Belastungsäquivalenzen mit Rücksicht auf gleichmäßige Verordnungslasten, Zeitschr. des Oesterr. Ing.- u. Arch.-Vereins 1897, S. 377, 393. – [19] Handbuch der Ingenieurwissenschaften, Bd. 2, Brückenbau, 2. Abt., Leipzig 1901, S. 22, 28, 33, 34, 302. – [20] Ostenfeld, Technische Statik, Leipzig 1904, S. 65. – S.a. Dimensionenberechnung, Grenzwerte, Verkehrslast.

Weyrauch.

Fig. 1., Fig. 2.