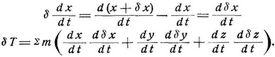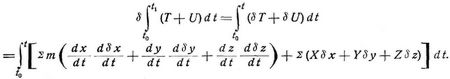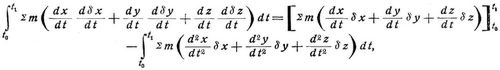Prinzip von Hamilton

Prinzip von Hamilton. Es ist dies ein Satz, mit Hilfe dessen die Bewegungsgleichungen eines Punktsystems, ähnlich wie mit Hilfe des d'Alembertschen Systems, aufgestellt werden können. Er setzt jedoch die Existenz einer Kräftefunktion U voraus, nämlich einer Funktion, deren Differential nach den Koordinaten

ist, wenn X, Y, Z die Komponenten der am Punkte (x y z) angreifenden Kraft sind und die Summation sich auf alle Punkte des Systems bezieht. Das Prinzip lautet: Wenn die Lagen des Systems zu den Zeiten t₀ und t₁ fest gegeben sind, T die lebendige Kraft (kinetische Energie = ¹/₂ Σ m v²) und U die Kräftefunktion bedeutet und das Zeichen δ sich auf unendlich kleine Aenderungen der Koordinaten der Punkte bezieht, die mit den Bedingungen des Systems verträglich sind, so ist für die Bewegung des Systems

wobei die den Zeiten t₀, t₁ entsprechenden Aenderungen gleich Null sind und die unabhängige Variable t keine Aenderung erleidet.

Es ist nämlich, wenn

die Komponenten der Geschwindigkeit des Punktes (x y z) sind, die Akzente also Differentiationen nach der Zeit bedeuten:

oder, da ist,

Daher hat man für die Aenderung des Integrals, dessen Grenzen feste Werte sind:

Nun liefert die partielle Integration:

und da an den Grenzen t₀, t₁ wegen der fest gegebenen Lage des Systems die Aenderungen δ x, δ y, δ z aller Koordinaten Null sind, so verschwindet der Wert des ersten eingeklammerten Gliedes der rechten Seite und bleibt

Wenn man dies einsetzt, erhält man

Nach dem d'Alembertschen Prinzip (s. S. 240) ist aber für alle mit den Bedingungsgleichungen des Systems verträglichen Verschiebungen

folglich wird unter dieser Bedingung

[243] Hiermit ist das Hamiltonsche Prinzip auf das d'Alembertsche Prinzip zurückgeführt. Es ist indessen spezieller als dieses, insofern es die Existenz einer Kräftefunktion voraussetzt. Diese Kräftefunktion kann jedoch die Zeit auch explizite enthalten, da die Aenderungen δ sich nicht auf sie beziehen. Ungeachtet dieser Beschränkung und des Umstandes, daß seine Anwendung die Variationsrechnung voraussetzt, ist es doch von großem Nutzen, da in demselben die Wahl der Koordinaten frei gelassen ist und man daher mit seiner Hilfe die Aufstellung der Bewegungsgleichungen für andre als rechtwinklige Koordinaten leichter erhält als mit Hilfe des d'Alembertschen Prinzips. Insbesondere dient das Hamiltonsche Prinzip zur Aufstellung der Bewegungsgleichungen in der zweiten Lagrangeschen Form (s. Differentialgleichungen der Bewegung, Bd. 2, S. 763).

Literatur: Hamilton, W.R., On a general method in dynamics etc., Philosophical Transactions of the Royal Soc. of London 1834, S. 247–308, und Second essay on a general method in dynamics, ebend. 1835, S. 95–144; Jacobi, Vorlesungen über Dynamik, herausgegeben von Clebsch, Berlin 1866, S. 58; Schell, Theorie der Bewegung und der Kräfte, Leipzig 1879, Bd. 2, S. 554.

(† Schell) Finsterwalder.