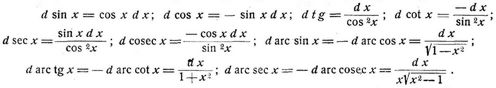Differentialrechnung

Differentialrechnung, die Rechnung mit Differentialen und Differentialquotienten, bildet zusammen mit der Integralrechnung (s.d.) die sogenannte höhere Analysis (Infinitesimalrechnung).

1. Bildung der Differentialen und Differentialquotienten.

a) Bei der Berechnung des Grenzwerts

ist zu beachten, daß höhere Potenzen von Δx vernachlässigt werden dürfen, z.B.

Ferner ist dC = 0 (wenn C eine Konstante ist), d(C · u) = Cdu; d (u + v + ...) = du + da + ...; d (u · p) = vdu = udv; d u/v = (vdu – udv) / v².

b) Formeln zur Bildung von Differentialen:

(wo e die Basis des natürlichen Logarithmensystems); dlx = dx/x (wo lx natürlicher Logarithmus);

(wo log_ax Logarithmus zur Basis a);

Ist ferner y = f(x), u = φ(y), also u die Funktion einer Funktion, so ist

z.B. u = l sin x. Man setzt sin x = y, also

Solche Potenzen, deren [766] Basis und Exponent veränderlich sind, verwandelt man in Exponentialfunktionen, z.B. x^x = (e^lx)^x = e^xlx; dx^x = e^xlx (lx + 1)dx = x^x (lx + 1)dx.

c) Zur Bestimmung des Differentialquotienten einer impliziten Funktion hat man einfach die Gleichung, die dieselbe bestimmt, zu differenzieren, z.B. y³ + x²y – x³ = 0 gibt

2. Anwendungen der Differentialrechnung bestehen in Reihenentwicklungen der Funktionen (s. Reihen), Berechnung unbestimmter Formen, Maxima und Minima (s.d. und Variationsrechnung), Partialbruchzerlegung gebrochener Funktionen (s. Partialbrüche). Hierzu kommen die geometrischen Anwendungen auf die Untersuchung von ebenen Kurven, Raumkurven und Flächen.

Literatur: Von den untengenannten Werken eignet sich [1] zur elementaren Einführung; [2], [3] und [22] sind beliebte Lehrbücher; [4] nimmt mehr einen funktionentheoretischen Standpunkt ein; [5] ist ein empfehlenswertes kleines Repetitionsbuch, [6]–[8] Uebungsbücher. Die geometrischen Anwendungen behandeln [9], [10], [25]–[28] sowie [24] Bd. 3, solche auf Naturwissenschaft und Technik [11], [12], [18], [20] und [23]. – [1] Götting, Einleitung in die Analysis, Berlin 1880. – [2] Stegemann, M., Grundriß der Differential- und Integralrechnung, Bd. 1, 10. Aufl., Hannover 1903. – [3] Serret, J.A., Lehrbuch der Differential- und Integralrechnung, deutsch von Harnack, Bd. 1, 2. Aufl., Leipzig 1897. – [4] Stolz, Grundzüge der Differential- und Integralrechnung, 1, Leipzig 1893. – [5] Derer, Repetitorium der Differential- und Integralrechnung, 4. Aufl., Berlin 1899. – [6] Dölp, H., Aufgaben zur Differential- und Integralrechnung, 9. Aufl., Gießen 1901. – [7] Schlömilch, O., Uebungsbuch zum Studium der höheren Analysis, Bd. 1, 4. Aufl., Leipzig 1888. – [8] Sohncke, Aufgaben aus der Differential- und Integralrechnung, I, 6. Aufl., Halle 1903. – [9] Darboux, G., Leçons sur la theorie generale des surfaces et les applications géométriques du calcul infinitesimal, I-IV, Paris 1887–96. – [10] Joachimsthal, F., Anwendungen der Differential- und Integralrechnung auf die allgem. Theorie der Flächen und der Linien doppelter Krümmung, herausg. von Natani, 3. Aufl., Leipzig 1890. – [11] Fuhrmann, A., Naturwissensch. Anwendungen der Differentialrechnung, 2. Aufl., Berlin 1900. – [12] Nernst, W., und Schönfließ, A., Kurzgefaßtes Lehrbuch der Differential- und Integralrechnung mit besonderer Berücksichtigung der Chemie, 3. Aufl., München 1901. – [13] Czuber, E., Vorlesungen über die Differential- und Integralrechnung, I, Leipzig 1898. – [14] Fricke, A., Hauptsätze der Differential- und Integralrechnung, I-III, Braunschweig 1897–1903. – [15] Genocchi, A., Differentialrechnung und Anfangsgründe der Integralrechnung, deutsch von Bohlman und Schepp, Leipzig 1899.– [16] Junker, F., Höhere Analysis, I, 2. Aufl., Leipzig 1902. – [17] Junker, F., Repetitorium und Aufgabensammlung zur Differential- und Integralrechnung, I, Leipzig 1902. – [18] Lorentz, H.A., Lehrbuch der Differential- und Integralrechnung, deutsch von Schmidt, Leipzig 1900. – [19] Meyer, F.W., Differential- und Integralrechnung, I, Leipzig 1901. – [20] Perry, J., Höhere Analysis für Ingenieure, deutsch von Fricke und Süchting, Leipzig 1902. – [21] Schlotke, J., Lehrbuch der Differential- und Integralrechnung, Leipzig 1903. – [22] Sturm, C., Lehrbuch der Analysis, deutsch von Groß, I, Berlin 1897. – [23] Fuhrmann, A., Bauwissenschaftliche Anwendungen der Differentialrechnung, II, Berlin 1898–99. – [24] Meyer, A., und Haas, A., Lehrbuch der Differentialrechnung, I-III, Stuttgart 1888–94. – [25] Bianchi, L., Vorlesungen über Differentialgeometrie, deutsch von Lukat, I-III, Leipzig 1896–99. – [26] Cefäro, E., Vorlesungen über natürliche Geometrie, deutsch von Kowalewski, Leipzig 1901. – [27] Klein, F., Anwendungen der Differential- und Integralrechnung auf Geometrie, I-II, Leipzig 1901–02. – [28] Scheffers, G., Anwendungen der Differential- und Integralrechnung auf Geometrie, 2 Bde., Leipzig 1901–02.

Wölffing.