Verzahnungen

Verzahnungen bewirken an Zahnradgetrieben Kraft- und Bewegungsübertragung, in Kapselwerken Abdichtung gegen Rückströmung.

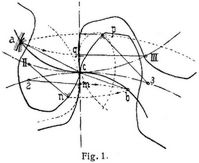
Sollen zwei Zahnräder (Fig. 1) im allgemeinen Fall mit gleichmäßiger Geschwindigkeitsübertragung, nämlich so zusammen arbeiten, daß ihre Teilkreise abrollen, ohne zu gleiten, so muß sich in jedem Augenblick das eine Rad relativ zum andern derart bewegen, daß es sich um den augenblicklichen Berührungspunkt c der Teilkreise dreht. Wenn nun an beliebiger Stelle, z.B. in a, zwei Zahnflanken beider Räder sich berühren, so müssen sich auch diese augenblicklich um c drehend bewegen, d.h. die Berührung muß normal zu a c stattfinden. Darum kann ein Zahnflankenstück nur in solcher Stellung richtig arbeiten, bei welcher seine Normale durch c geht. So wird der Punkt p zum Eingriff kommen, wenn die auf der Zahnflanke in p errichtete Normale p 3 sich mit dem unteren Rade so weit gedreht hat, daß 3 nach c gekommen ist, wobei a c = p 3 ist. Hierdurch ist ein Punkt a der Eingrifflinie bestimmt. Die Linie ac ist beiden Rädern augenblicklich gemeinsam. Dreht man nun das obere Rad mit seiner Linie a c um das Bogenstück c III = c 3 zurück, so kommt ac nach q III und die Zahnflanke in q muß normal zu q III verlaufen. Ebenso kommen die Punkte m und n in b zum Eingriff, während die beiden Normalen m 2 und n II zugleich nach b c gekommen sind. Nach diesem von Reuleaux angegebenen Verfahren der allgemeinen Verzahnung kann man zu einer gegebenen Zahnform, vorausgesetzt, daß deren Normalen den Teilkreis schneiden, die Eingrifflinie und die zugehörige Zahnform ableiten. Die Richtung von c nach einem Punkte der Eingrifflinie gibt die Krastrichtung (ohne Rücksicht auf die Zahnflankenreibung) an.

Die Systeme sind durch die Form der Eingrifflinie bestimmt.

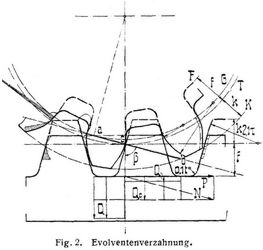
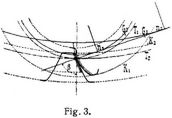
Die fast ausschließlich benutzte Evolventenverzahnung (Bd. 3, S. 520) hat eine geradlinige Eingrifflinie, die schräg durch den Berührungspunkte der Teilkreise T geht, in der Regel mit der Neigung ß = 75°, nach amerikanischem Gebrauch mit 71¹/₂° oder tg ß = 3. Die die Gerade berührenden Grundkreise G sind im Verhältnis sin ß kleiner als die Teilkreise. Bei der Abwicklung der Geraden auf einem ihrer Grundkreise beschreibt jeder Punkt eine Evolvente[792] als Zahnkurve, die nur nach der Größe der Grundkreise verschieden ausfällt. Für die Zahnstange (mit unendlich entferntem Grundkreise) geht sie in eine zur Eingrifflinie senkrecht stehende gerade Linie über (Fig. 2). Bei Hohlrädern wird die Zahnflanke konkav (Fig. 3). Zur Aufzeichnung [6] der Evolvente trägt man (nach Bd. 3, S. 520, Fig. 1) auf der Geraden und dem Grundkreise vom Berührungspunkte aus gleiche Strecken ab, die man im Verhältnis zur Krümmung des Kreises nicht zu groß wählt, und schlägt mit dem Abstande des Punktes c (oder eines andern Punktes der Geraden) von je einem Teilpunkte der Geraden einen Bogen von dem zugehörigen Teilpunkte des Grundkreises aus; die Umhüllende der Bögen ist die Evolvente. Sie steht auf dem Grundkreise senkrecht auf und würde weiterhin mit einem symmetrisch liegenden Zweige wieder aufsteigen. Zur Uebertragung der Kurve auf eine Reihe von Zähnen ersetzt man sie durch Kreisbogenstücke, auch bei der Herstellung von Werkzeugen, Modellen und Lehren [8]. Grants Odontograph [8] ist eine Tabelle ziemlich passender Radien (Fig. 2), deren Mittelpunkte auf dem Grundkreise liegen, der für ß = 75° ungefähr ¹/₆₀ des Teilkreisdurchmessers vom Teilkreise entfernt ist. Die Zahlenreihe verläuft allerdings sprungweise und läßt sich durch folgende Formeln [3] ausgleichen: Räder mit der Teilung t = τ n von 10 bis 36 Zähnen erhalten für die Kopfkurve den Radius (1,5 + 0,085 z) τ und zwischen Teilkreis und Grundkreis den Radius 0,09 z τ; Räder von 37 bis 200 Zähnen erhalten vom Kopfkreis bis zum Grundkreis den Radius (1,0 + 0,085 z) τ. An der Zahnstange soll die obere Hälfte der Kopfkurve mit einem Radius von 2,1 τ abgerundet werden, dessen Mittelpunkt im Teilkreise liegt; der Bogen schließt sich an die gerade Flanke in der Höhe von 2,1 τ cos 75° = 0,54 τ über dem Teilriß an.

Innerhalb des Grundkreises zieht man die Fußflanke radial bis zum Fußkreis F und schließt sie mit 0,1 t oder 0,3 τ als Abrundungsradius an diesen an. Da die innerhalb des Grundkreises liegende Flanke nicht richtig arbeiten kann, vielmehr, wenn sie mit dem Kopf des Gegenzahnes zusammentrifft, von diesem geschlagen wird, weil der sogenannte gefährliche Weg der Kopfhäute den geraden Zahnfuß durchschneidet, muß man darauf achten, den Fehler zu vermeiden. Er tritt ein, wenn der Berührungspunkt von Eingrifflinie und Grundkreis im Bereich der Zähne des Gegenrades liegt, insbesondere am kleineren Rade in Verbindung mit einem großen, einer Zahnstange oder gar einem Hohlrad, nämlich wenn die kleinere Zähnezahl bei der

ist. In solchem Falle kann man die Köpfe des Gegenrades abkürzen, so daß sein Kopfkreis äußerstenfalls durch jenen Berührungspunkt geht (Fig. 2), wobei der Fußkreis des kleinen Rades um ein gleiches Maß weiter nach außen verlegt werden kann; oder man wählt einen kleineren Neigungswinkel für die Eingrifflinie bis auf ß = 60°; oder man unterscheidet den Zahnfuß, indem man die Zahnflanke nicht radial, sondern parallel zur Mittellinie der Lücke zieht [9]; oder benutzt eine besondere Lückenprofilierung (Bd. 6, S. 233); oder man rundet den Kopf des Gegenzahnes nach Maßgabe der Geradflankenverzahnung.

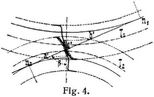
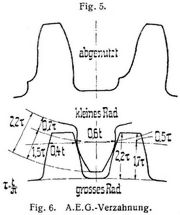
Rückt man zwei Evolventenräder etwas auseinander (Fig. 4), so arbeiten die auf den Grundkreisen errichteten Evolventen richtig zusammen längs der unter kleinerem Winkel ß liegenden gemeinsamen Tangente als Eingrifflinie, jedoch mit abgekürzter Eingriffdauer. Ebenso bleibt die Kämmung richtig, wenn man die Zahnräder näher aneinander rückt, falls sich die Flanken nicht etwa durch Abnutzung (vgl. Fig. 5) verändert haben [1]. Diese vorzügliche Eigenschaft der Evolventen benutzt man gern, indem man beim Einbau die Räder gerade so dicht zusammenstellt, daß die Zähne ohne Flankenspielraum, aber noch ohne Klemmen ineinander laufen.

Längs der Eingrifflinie kommt der zwischen den beiden Kopfkreisen enthaltene Abschnitt a b c als Eingriffstrecke zur Wirkung und ein gleichgroßer Eingriffbogen auf dem Grundkreise, dem ein im Verhältnis 1 : sin ß größerer Eingriffbogen auf dem Teilkreis entspricht, z.B. a b/sin 75° = 1,035 a b. Die Eingriffdauer, nämlich das Verhältnis des Eingriffbogens[793] des Teilkreises zur Teilung muß größer als 1 sein, damit jedes Zahnpaar mindestens so lange in Eingriff bleibt, bis das folgende eingesetzt hat. Man erstrebt eine Eingriffdauer über 2 bei großer Geschwindigkeit durch Annahme einer reichlichen Zähnezahl.

Im Beginn des Eingriffs stemmt sich der Kopf des getriebenen Rades mit seiner Kopfhäute gegen die Fußflanke des treibenden Zahnes, noch bevor er sich unter der Wirkung des Zahndruckes elastisch deformiert hat. Hiergegen empfiehlt sich, die Kopfflanke an ihrem äußersten Teil etwas mehr zu krümmen, als der genauen Evolventenform entspricht [3], unter Einhaltung genügender Eingriffdauer. Ueberhaupt wirkt die Schiebung vor der Zentralen nicht so günstig wie das Ausstreichen hinter ihr. Der in die Richtung der Eingrifflinie fallende Normaldruck der Zahnflanken hält sich bei Evolventen konstant auf P/sin ß für P kg Umfangskraft im Teilkreis; doch erhöht sich der die Räder auseinander drängende radiale Seitendruck Q₀ = P ctg ß (mit ctg 75° = 0,268) infolge der Reibung der Zahnflanken vor der Zentralen fast auf ¹/₂ P, ermäßigt sich aber dahinter auf einen geringen Betrag, wie in Fig. 2, für μ = 0,2 berechnet, an der Zahnstange eingezeichnet ist.

Die Abnutzungscharakteristik oder die Reibungsarbeit an den einzelnen Punkten der Zahnflanken ist abhängig vom Normaldruck, der Reibziffer und der relativen Gleitung, die aus dem Unterschied der bei kleinen Winkeldrehungen zum Angriff kommenden Teilstrecken der Zahnkurven zu bestimmen ist. Fig. 2 enthält rechts eine gröbere Einteilung der Zahnkurven für je ein Viertel der Teilung und links die von Büchner [4] für 16 auf 48 Zähne berechnete Abnutzungscharakteristik, die im Teilkreise gleich Null und im Grundkreise unendlich groß wird. Praktisch verläuft die Abnutzung unter Veränderung der Evolvente in eine doppelt geschwungene Kurve (Fig. 5, Gußeisenrad vom Heilbronner Wasserwerk), indem neben einem stark auf Abnutzung beanspruchten Punkte die Nachbarpunkte zur Mitwirkung kommen, und außerdem die Kopfhäute den Fuß des Gegenzahnes ausschabt. Beim ersten Einlaufen der Räder schlagen sich zunächst die vorstehenden Flächenteile der Flanken nieder, weil schon bei unmeßbar kleinen Abweichungen von der richtigen Zahnform, wie bei dem Ersatz einer Evolvente durch seinen dazu passenden Kreisbogen, starke Aenderungen der Geschwindigkeit und hohe Beschleunigungsdrucke auftreten [7].

Für Evolventensatzräder benutzt man bei ß = 75° gewöhnlich eine Kopfhöhe k = 0,3 t und eine Fußhöhe f = 0,4 t oder k = 1,0 τ und f = 11/6 τ, unter der angegebenen Beschränkung. Die praktisch bewährte Evolventensatzräderverzahnung von Paul Hoppe, die nicht vom Teilkreis ausgeht, sondern den zusammenarbeitenden Rädern gleiche Teilung auf dem Grundkreise gibt, wird in [9] ausführlich dargestellt.

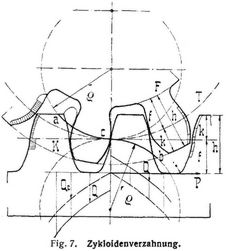
Einzelräder baut man paarweise ohne Rücksicht auf allgemeine Verwendbarkeit unter Bevorzugung des hinter der Zentralen liegenden Eingriffs und mit annähernd gleicher Stärke der Zähne im Fußkreis [5]. Nach einem Vorschlag von Keller hat die Allgemeine Elektrizitätsgesellschaft in Berlin für die Uebersetzung von Elektromotoren ins Langsame die in Fig. 6 eingeschriebenen Maßverhältnisse angenommen, als sogenannte A.E.G.-Verzahnung [2]. Zur Erzielung ruhigen Ganges, z.B. beim Antrieb einer Tischhobelmaschine mit Zahnstange, kann man auf den Eingriff vor der Zentralen ganz verzichten, indem man der Stange nur niedrige, abgerundete Köpfe gibt und für das eingreifende Zwischenrad große Kopfhöhe oder mindestens 40 Zähne wählt.

Die Zykloidenverzahnung (Fig. 7) hat (nach Bd. 2, S. 486) eine aus zwei Kreisbogen bestehende Eingrifflinie, nämlich die Rollkreise, die außerhalb und innerhalb auf dem Teilkreise abrollend, mit einem ihrer Punkte die Zykloiden beschreiben. Zur Aufzeichnung [6] trägt man gleiche, nicht zu große Strecken auf Teilkreis und Rollkreis vom Berührungspunkte c aus mehrmals ab und schlägt mit der Entfernung des Punktes c von einem Teilpunkte des Rollkreises einen Bogen um den zugehörigen Teilpunkt des Teilkreises; die Umhüllende der Kreisbögen ist eine Epizykloide außerhalb und eine Hypozykloide innerhalb des Teilkreises, an der Zahnstange (Fig. 7) eine Orthozykloide oberhalb und unterhalb des Teilriffes. Die Eingriffstrecke a c b wird durch die Kopfkreise begrenzt. Der Eingriffbogen auf dem Teilkreise ist gleich groß. Die Eingriffdauer als das Verhältnis von a c b zur Teilung muß größer als 1 sein. Die Fußkurven, die sich mit dem Abrundungsradius von 0,1 t an den Fußkreis anschließen, kommen nur so weit zum Angriff, wie die Punkte a und b innerhalb der Teilkreise liegen. In Fig. 7 sind rechts die auf je ¹/₄ t angreifenden Strecken der Zahnkurven abgeteilt, links ist die für 16 auf 48 Zähne berechnete Abnutzungscharakteristik [4] angetragen und das von der Kopfhäute im Fuß des Gegenzahnes allmählich auszuschabende Stück angedeutet. Der Normaldruck fällt während der Berührung in der Zentralen gerade in die Umfangsrichtung, bei a und b in die Richtung a c b. Dementsprechend steigt der Seitendruck Q₀ von Null in der Zentralen nach vorn und hinten an; mit Einrechnung der Reibung für μ = 0,2 erhöht sich der Seitendruck Q im Punkte a auf 0,7 P und verursacht beim Durchgang durch die Zentrale einen Druckwechsel. Hiernach verläuft die Kraftübertragung nicht so sanft, wie man gewöhnlich annimmt. Die Räder müssen, um richtig zu arbeiten, genau auf Berührung der Teilkreise eingestellt werden. Gegenüber den Evolventen bleibt als Vorteil nur der die Abnutzung mildernde Umstand der Anschmiegung erhabener und hohler Flanken.

[794] Für Satzräder wählt man den Radius der Rollkreise je zu ς = ⁷/₈ t oder 2,75 τ, die Kopfhöhe k = 0,3 t oder 1,0 τ, die Fußhöhe f = 0,4 t oder ⁷/₆ τ auch bis ⁵/₄ τ. Für Einzelräder nimmt man wohl den einen oder andern Rollkreis größer an, zur Erhöhung der Eingriffdauer, wobei allerdings das nutzbare Stück der Zahnfußkurve kürzer ausfällt. Wenn der Rollkreis gerade halb so groß wie der Teilkreis ist, wird die Fußkurve eine radiale gerade Linie; zweckmäßig benutzt man für Uhrwerkräder und Holzzähne (Bd. 5, S. 113 und 128) zur Vermeidung der radialen Unterschneidung der Zahnfüße als Zahnkurven Aequidistanten als Geradflankenverzahnung (Bd. 4, S. 396). Wenn der Rollkreis gleich dem Teilkreis ist, bleibt der sonst die Fußkurve beschreibende Punkt im Teilkreise liegen und gleitet längs des Teilkreisbogens als Eingrifflinie an der Kopfkurve des Gegenzahnes, als Punktverzahnung (Bd. 7, S. 297). Mit Aequidistanten im Abstande der halben Zahnstärke erhält man für den Punkt einen Kreis (s. Triebstockverzahnung). Für eine Zahnstange mit Triebstöcken beschreibt die Triebstockmitte (als Punkt auf dem geraden Teilriß als Rollkreis) statt der Zykloide eine Evolvente auf dem Teilkreise des Rades und für eine auflaufende Gelenkkette (Bd. 5, S. 459) einen Kreisbogen.

Eine gemischte Verzahnung mit Zykloiden als treibenden Flanken und Evolventen mit ß = 53°, nämlich sin ß = 0,8, als Rückenflanken bildet die Daumenverzahnung (Bd. 2, S. 677); s.a. Hebedaumen (Bd. 5, S. 1).

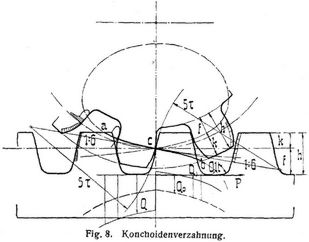
Konchoidenverzahnung (Fig. 8) mit Konchoiden als Eingrifflinie ist als ein zwischen Evolventen- und Zykloidenverzahnung vermittelndes System vorgeschlagen [3], bestimmt durch kreisbogenförmige Kopf- und Fußkurven für die Zähne der Zahnstange vom Radius 5 τ, deren Mittelpunkte auf einer mit der Neigung 1 : 6 durch den Teilriß gehenden Geraden liegen. Die nach Fig. 1 zu entwickelnden Radzahnkurven schmiegen sich erhaben und hohl aneinander und gehen schräg durch die Teilkreise, die beim Einbau der Räder auf Berührung einzustellen sind. Die Seitendrucke halten günstige Mittelwerte zwischen denen der andern Systeme ein, ebenso die Abnutzungscharakteristik, deren Höchstwerte, berechnet für 16 auf 48 Zähne [4], sich für Zykloiden, Konchoiden und Evolventen wie 2,6 : 6,8 : ∞ verhalten. Für die Zahnhöhen sind in [3] mit Rücksicht auf Fettigkeit im allgemeinen niedrige Werte in Vorschlag gebracht, doch kann man für Konchoidensatzräder bis herab zu neun Zähnen die sonst üblichen Maße ohne weiteres anwenden. Triebe von vier bis acht Zähnen sind besonders auszubilden.

Literatur: [1] Zeitschr. d. Ver. deutsch. Ing. 1894, S. 168/170. – [2] Ebend. 1899, S. 1417/1569. – [3] Ebend. 1900, S. 304 bis 311. – [4] Ebend. 1902, S. 159 bis 284. – [5] Ebend. 1903, S. 315. – [6] Ebend. 1903, S. 690, 713, 739 und 854 bis 857; 1905, S. 752. – [7] Ebend. 1905, S. 163 bis 167. – [8] Katalog von Friedrich Stolzenberg & Co. in Berlin-Reinickendorf. – [9] Verhandl. des Vereins für Gewerbfleiß 1909, S. 245 s.

Lindner.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.

Fig. 5., Fig. 6.

Fig. 7.

Fig. 8.